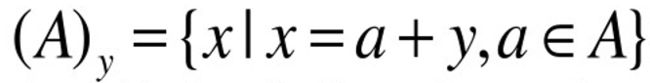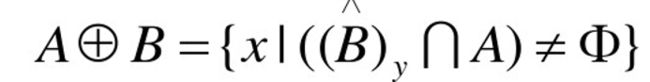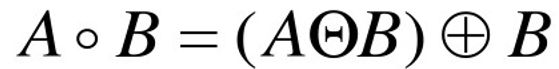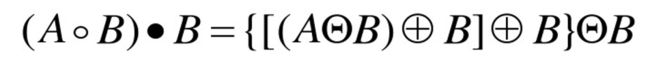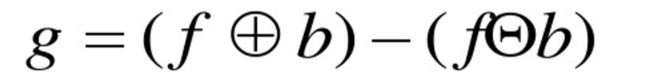冈萨雷斯《数字图像处理》学习笔记（九）形态学图像处理
目录
序言
一、集合论基础
1、集合的子集与相等
2、集合的基本运算符
3、集合的反射和平移
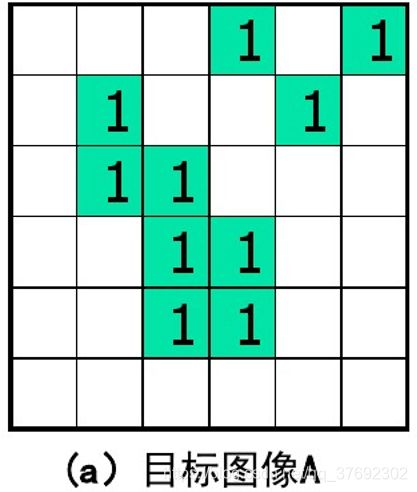
二、二值形态学的基本运算
1、腐蚀
2、膨胀
3、膨胀与腐蚀运算的对偶性
3、开运算与闭运算
4、一些基本的形态学算法
三、二值形态学图像处理
1、形态滤波
2、边界提取
3、区域填充
4、骨架提取
5、物体识别
四、灰度形态学基本运算
1、灰度腐蚀
2、灰度膨胀
3、灰度开运算和灰度闭运算
五、灰度形态学处理算法
1、形态学平衡
2、形态学平衡
3、top—hot变换
序言
形态学图像处理
将数学形态学作为工具从图像中提取表达和描绘区域形状的有用图像分量，如边界、骨架和凸壳等。最常见的有腐蚀和膨胀、开操作和闭操作、击中和击不中变换。本章一开始将讨论二值图像 的处理，之后将扩展到 灰度图像
形态学图像分析基本步骤
■提出所要描述的物体几何结构模式,即提取几何结构特征;
■根据结构模式选择相应的结构元素(简单又有最强的表现力) ;
■用选定的结构元对图像实行击中与否(HMT,Hit-Miss-Transform)变换，便得到比原始图像更显著突出物体特征信息的图像。如赋予相应变量，还可得到定量描述;
■经过形态学变换后的图像突出我们所需的信息，从而可以方便提取信息。
■综上，HMT是MM图像分析的核心运算。
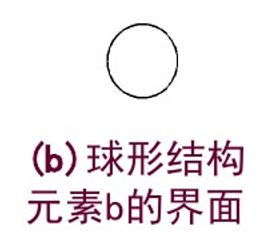
在形态学算法设计中，结构元的选择十分重要，其形状、尺寸的选择是能否有效提取信息的关键。选择的几个基本原则:
■结构元必须在几何上比原图像简单，且有界;
■当选择性质相同或相似的结构元时，以选择极限情况为宜;
■结构元的凸性很重要，对非凸子集，由于连接两点的线段大部分位于集合的外面，故用非凸子集作为结构元将得不到什么信息。
数学形态学进行图像处理的基本思想是:用具有一定形态的结构元素探测目标图像，通过检验结构元素在图像目标中的可放性和填充方法的有效性，来获取有关图像形态结构的相关信息,进而达到对图像分析和识别的目的。
一、集合论基础
1、集合的子集与相等
且当且仅当
和同时成立时，称集合A和B集合相等。
2、集合的基本运算符
集合的并
集合的交
集合的补
集合的差
3、集合的反射和平移
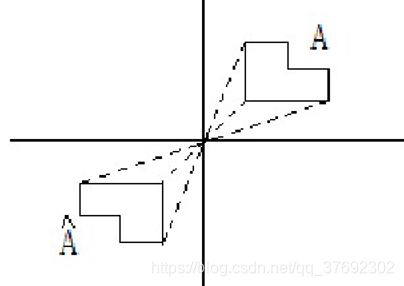
集合的反射
由集合A中所有元素相对于原点的反射元素组成的集合称为集合A的反射，记为 
。
其中x表示集合A中的元素a对应的反射元素。
集合的反射图示：
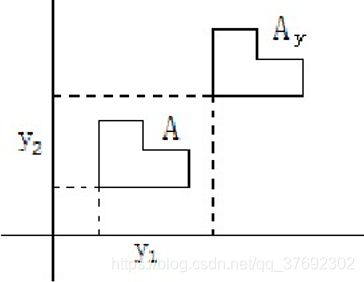
集合的平移
由集合A中所有元素平移y= (y1, y2) 后组成的元素集合称为集合A的平移，记为
其中，x表示集合A中的元素a平移y后形成的元素。
集合平移图示：
二、二值形态学的基本运算
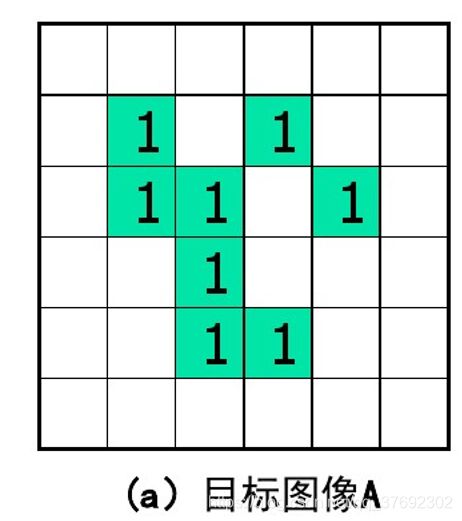
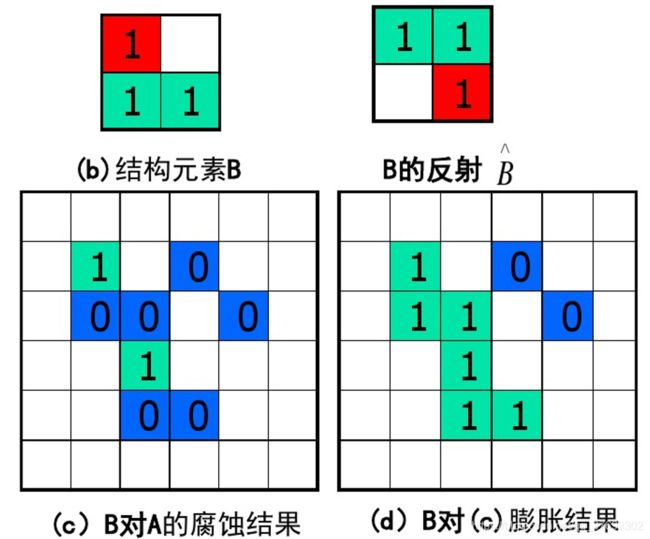
1、腐蚀
设A为目标图像，B为结构元素，则目标图像A被结构元素B腐蚀可定义为:
其中，y是一个表示集合平移的位移量。
腐蚀运算的含义是:每当在目标图像A中找到一个与结构元素B相同的子图像时，就把该子图像中与B的原点位置对应的那个像素位置标注为1， 图像A上标注出的所有这样的像素组成的集合，即为腐蚀运算的结果。简而言之，腐蚀运算的实质就是在目标图像中标出那些与结构元素相同的子图像的原点位置的像素。
注意，结构元素中的原点位置可以不为1,但要求目标图像中的子图像与结构元素B的原点对应的那个位置的像素值是1。
腐蚀运算的基本过程是:把结构元素B看作为一个卷积模板，每当结构元素平移到其原点位置与目标图像A中那些像素值为“1”的位置重合时，就判断被结构元素覆盖的子图像的其它像素的值是否都与结构元素相应位置的像素值相同;只有当其都相同时，就将结果图像中的那个与原点位置对应的像素位置的值置为“1”，否则置为0。
注意:当结构元素在目标图像上平移时，结构元素中的任何元素不能超出目标图像的范围。
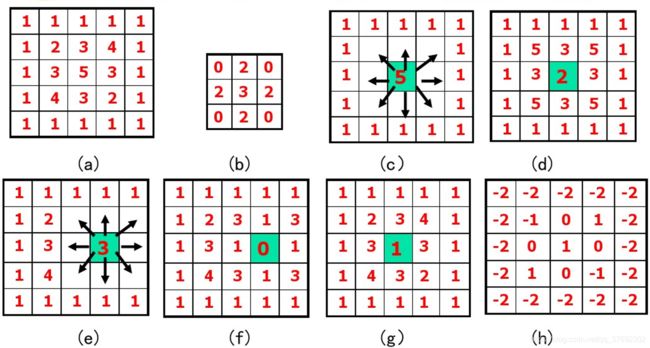
腐蚀举例：
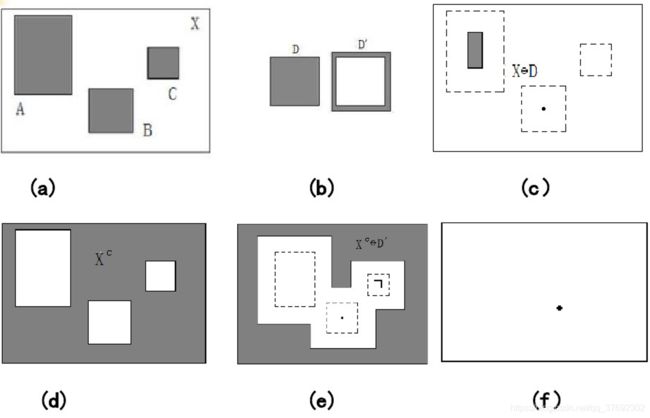
应用：利用腐蚀算法识别物体
2、膨胀
设A为目标图像，B为结构元素，则目标图像A被结构元素B膨胀可定义为：
其中，y是一个表示集合平移的位移量。
膨胀的含义:先对结构元素B做关于其原点的反射得到反射集合
, 然后再在目标图像A上将平移y, 则那些平移后与目标图像A至少有1个非零公共元素相交时对应的的原点位置所组成的集合，就是膨胀运算的结果。
膨胀运算的基本过程:
(1)求结构元素B关于其原点的反射集合;
(2)每当结构元素在目标图像A.上平移后，结构元素与其覆盖的子图像中至少有一个元素相交时,就将目标图像中与结构元素的原点对应的那个位置的像素值置为“1”， 否则置为0。
注意: (1)当结构元素中原点位置的值是0时，仍把它看作是0；而不再把它看作是1。
(2)当结构元素在目标图像上平移时，允许结构元素中的非原点像素超出目标图像范围。
膨胀举例：
应用：利用膨胀运算填充目标区域中的小孔
3、膨胀与腐蚀运算的对偶性
即，对目标图像的膨胀运算，相当于对图像背景的腐蚀运算操作；对目标图像的腐蚀运算，相当于对图像背景的膨胀运算操作。
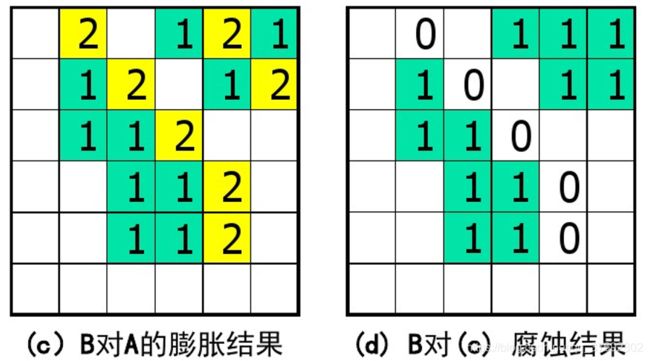
腐蚀运算与膨胀运算的对偶性示例：
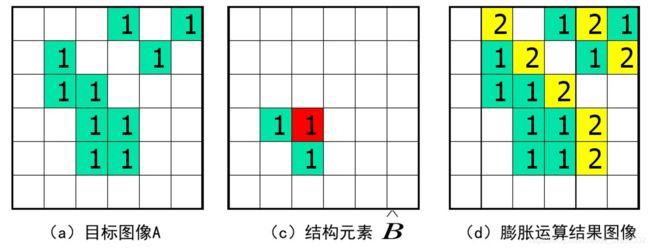
3、开运算与闭运算
开运算
使用同一个结构元素对目标图像先进行腐蚀运算，然后再进行膨胀运算称为开运算。
结构元素B对目标图像A的开运算定义为：
举例：
闭运算
使用同一个结构元素对目标图像先进行膨胀运算，然后再进行腐蚀运算称为闭运算。
结构元素B对目标图像A的闭运算定义为：
举例：
开运算和闭运算的对偶性
闭运算可以使物体的轮廓线变得光滑，具有磨光物体内边界的作用；而开运算具有磨光图像外边界的作用。
4、一些基本的形态学算法
边界抽取(boundary extraction)
区域填充(region flling)
连接分量提取(extraction of connectedcomponents)
凸壳算法(convex hull)
细化(thinning)
粗化(thickening)
骨架(skeletons)
修剪(pruning)
三、二值形态学图像处理
1、形态滤波
2、边界提取
边界提取示例：
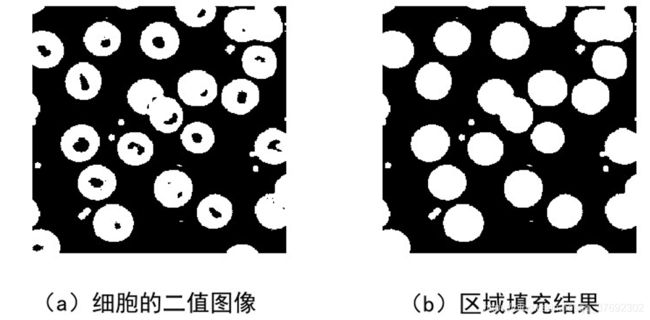
3、区域填充
对细胞图像的区域填充示例：
4、骨架提取
变体
1)细化
结果:在不破坏连通性的前提下，细化图像
算法实现:
1)做腐蚀操作，但不立刻删除像素，只打标记;
2)将不破坏连通性的标记点删掉；
3)重复执行，将产生细化结果
2)粗化
结果: 在不合并对象的前提下，粗化图像。
算法实现:
1)做膨胀操作，但不立刻添加像素，只打标记；
2)将不产生对象合并的标记点添加进来；
3)重复执行，将产生粗化结果
另一方案:将图像求反，执行细化，结果再求反
骨架提取实例：
5、物体识别
四、灰度形态学基本运算
灰度形态学是二值形态学向灰度空间的自然扩展。在灰度形态学中，分别用图像函数f (x, y)和b (x, y)表示二值形态学中的目标图像A和结构元素B,并把f (x, y)称为输入图像，b (x, y)称为结构元素，函数中的(x, y)表示图像中像素点的坐标。
二值形态学中用到的交和并运算在灰度形态学中分别用最大极值和最小极值运算代替。
1、灰度腐蚀
在灰度图像中，用结构元素b (x, y)对输入图像f (x, y)进行灰度腐蚀运算可表示为:
(f
b)(s,t) = min{f(s+x,t+ y)-b(x,y)I(s+ x),(t+ y)∈;(x,y)∈}
其中，和分别表示f (x, y)和b(x, y)的定义域。x和y必须位于结构元素的定义域之内，而平移参数(s+x)和(t+y)必须位于的f (x, y)的定义域之内。
与二值图像腐蚀运算不同的是:被移动的是输入图像f (x, y)函数而不是结构元素b (x, y)。
灰度腐蚀运算的特点：灰度腐蚀运算的计算是逐点进行的, 求某点的腐蚀运算结果就是:计算该点局部范围内各点与结构元素中对应点的灰度值之差，并选取其中的最小值作为该点的腐蚀结果。经腐蚀运算后， 图像边缘部分具有较大灰度值的点的灰度会降低，因此，边缘会向灰度值高的区域内部收缩。
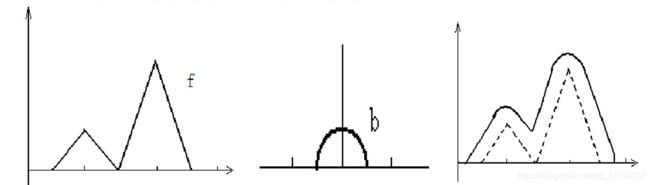
灰度腐蚀运算示例：
灰度腐蚀运算的一维函数形式：
利用结构元素b (x)对目标图像f (x)的腐蚀过程是:在目标图像的下方“滑动”结构元素，结构元素所能达到的最大值所对应的原点位置的集合即为腐蚀的结果。
腐蚀运算过程示意图：
2、灰度膨胀
在灰度图像中，用结构元素b (x, y)对输入图像f(x,y)进行灰度膨胀运算可表示为: 
其中，和分别表示f (x, y)和b (x, y)的定义域。X和y必须位于结构元素的定义域之内，而平移参数(s+x)和(t+y)必须位于的f (x, y)的定义域之内。
需要注意的是:二值膨胀运算中要求目标图像集合和结构元素集合相交至少有一个元素。
灰度膨胀运算的特点:灰度膨胀运算的计算是逐点进行的，求某点的膨胀运算结果就是计算该点局部范围内各点与结构元素中对应点的灰度值之和，并选取其中的最大值作为该点的腐蚀结果。经膨胀运算后，图像边缘部分得到了延伸。
灰度膨胀运算示例：
灰度膨胀运算的一维函数形式：
膨胀运算过程示意图：
3、灰度开运算和灰度闭运算
灰度开运算
用结构元素b对灰度图像f进行开运算可表示为:
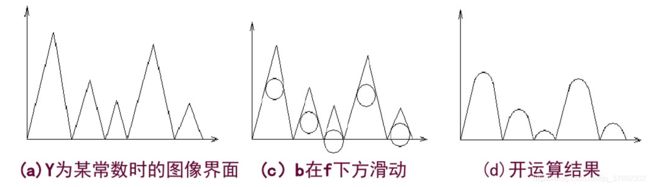
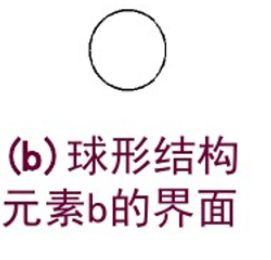
开运算可以通过将求出的所有结构元素的形态学平移都填入目标图像f下方的极大点来计算。如下图几何直观描述：
灰度闭运算
用结构元素b对灰度图像f进行闭运算可表示为: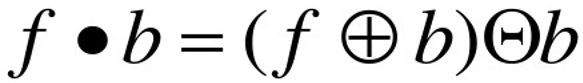
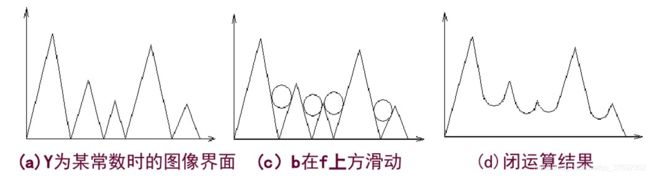
闭运算可以通过求出所有结构元素的形态学平移与目标图像.上方的极小值点来计算。如下图几何直观描述：
五、灰度形态学处理算法
1、形态学平衡
对添加椒盐噪声的Lena图像的形态学平滑：
2、形态学平衡
使用空间梯度算子对形态学梯度算子对Lena图像进行处理的结果：
3、top—hot变换
