算法专练：有序集合

1.1418. 点菜展示表

原题链接

        给你一个数组 orders，表示客户在餐厅中完成的订单，确切地说， orders[i]=[customerNamei,tableNumberi,foodItemi] ，其中 customerNamei 是客户的姓名，tableNumberi 是客户所在餐桌的桌号，而 foodItemi 是客户点的餐品名称。

        请你返回该餐厅的 点菜展示表 。在这张表中，表中第一行为标题，其第一列为餐桌桌号 “Table” ，后面每一列都是按字母顺序排列的餐品名称。接下来每一行中的项则表示每张餐桌订购的相应餐品数量，第一列应当填对应的桌号，后面依次填写下单的餐品数量

        注意：客户姓名不是点菜展示表的一部分。此外，表中的数据行应该按餐桌桌号升序排列。

        示例 1：

        输入：orders = [[“David”,“3”,“Ceviche”],[“Corina”,“10”,“Beef Burrito”],[“David”,“3”,“Fried Chicken”],[“Carla”,“5”,“Water”],[“Carla”,“5”,“Ceviche”],[“Rous”,“3”,“Ceviche”]]

        输出：[[“Table”,“Beef Burrito”,“Ceviche”,“Fried Chicken”,“Water”],[“3”,“0”,“2”,“1”,“0”],[“5”,“0”,“1”,“0”,“1”],[“10”,“1”,“0”,“0”,“0”]]

        示例 2：

        输入：orders = [[“James”,“12”,“Fried Chicken”],[“Ratesh”,“12”,“Fried Chicken”],[“Amadeus”,“12”,“Fried Chicken”],[“Adam”,“1”,“Canadian Waffles”],[“Brianna”,“1”,“Canadian Waffles”]]

        输出：[[“Table”,“Canadian Waffles”,“Fried Chicken”],[“1”,“2”,“0”],[“12”,“0”,“3”]]

        示例 3：

        输入：orders = [[“Laura”,“2”,“Bean Burrito”],[“Jhon”,“2”,“Beef Burrito”],[“Melissa”,“2”,“Soda”]]

        输出：[[“Table”,“Bean Burrito”,“Beef Burrito”,“Soda”],[“2”,“1”,“1”,“1”]]

        提示：

        1 <= orders.length <= 5 * 10^4

        orders[i].length == 3

        1 <= customerNamei.length, foodItemi.length <= 20

        customerNamei 和 foodItemi 由大小写英文字母及空格字符 ’ ’ 组成。
tableNumberi 是 1 到 500 范围内的整数。

        这道题其实并没有什么难度，就是模拟，我们要输出的信息有所有顾客点餐的种类，桌子编号和每张桌子点菜的数量。菜种类可以利用set来存储，而每张桌子每种菜点的次数则可以利用map来存储（因为有序就不能用unorder_map了），最后直接返回即可，因为这些数据结构都是有序的，不过还是有些需要注意的点的，在代码部分进行解释。

class Solution {
    int str_toint(const string& s){//string转换为int
        int ans=0;
        for(int i=0;i<s.size();++i){
            ans=ans*10+s[i]-'0';
        }
        return ans;
    }
    string to_str(int x){//int 转换为 string
        if(!x){
            return "0";
        }
        string ans;
        while(x){
            ans.push_back(x%10+'0');
            x/=10;
        }
        reverse(ans.begin(),ans.end());
        return ans;
    }
public:
    vector<vector<string>> displayTable(vector<vector<string>>& orders) {
        map<string,int> map[501];//map数组来存储每张桌子的的点餐数量
        set<string> s;//记录点餐种类
        int i;
        vector<vector<string>> ans;
        for(i=0;i<orders.size();++i){
            string name=orders[i][0];
            int tablenum=str_toint(orders[i][1]);
            //桌子编号是下标这里要先转换成int便于记录，在后面我们还要将他转换成string
            string food=orders[i][2];
            //点菜的种类
            map[tablenum][food]++;
            //直接对下标为talbenum的map进行操作，这里的food是key，每次遍历都对其加一
            s.insert(food);//set会自动去重，我们每次都加入菜名即可。
        }
        vector<string> head;
        //表头单独处理先加入Table，然后加入set中元素即可
        head.push_back("Table");
        for(auto it=s.begin();it!=s.end();++it){
            head.push_back(*it);
        }
        ans.push_back(head);
        //随后对每个编号的桌子进行处理
        for(i=1;i<=500;++i){
            vector<string> tmp;
            if(map[i].size()){
                tmp.push_back(to_str(i));
                for(auto it=s.begin();it!=s.end();++it){
                    tmp.push_back(to_str(map[i][*it]));
                }
                ans.push_back(tmp);
            }
        }
        return ans;
    }
};

2.363. 矩形区域不超过 K 的最大数值和

原题链接

给你一个 m x n 的矩阵 matrix 和一个整数 k ，找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。
题目数据保证总会存在一个数值和不超过 k 的矩形区域。
示例 1：
输入：matrix = [[1,0,1],[0,-2,3]], k = 2
输出：2
示例 2：
输入：matrix = [[2,2,-1]], k = 3
输出：3
提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-100 <= matrix[i][j] <= 100
-105 <= k <= 105

        很有意思的一个题，也是第一次见到这种类型的题目。看到矩阵区域和我第一时间想到的其实是二维前缀和，不过由于数据中存在负数所以这种方法不现实。

        回到本题来要解决这道题，我们直接进行枚举。对于一个m*n的矩阵，这里我们依次选取两列 l,r代表我们当前枚举的列范围。在列范围固定的情况下我们就从行开始枚举，从0到m行先求出每行的前缀和以及该范围内的前缀和，把他们放到一个数组中去，当求出了从[0,l] - >[m-1,r]这个范围内的矩阵每行的和之后，我们就去查找。

		for(int i=0;i<m;++i){
            for(int j=1;j<n;++j){
                matrix[i][j]+=matrix[i][j-1];
            }
            //这里是为了下面求在列范围内的行的前缀和方便，先求出每行的前缀和
        }
        for(l=0;l<n;++l){
            for(r=l;r<n;++r){
                int sum[maxn];
                sum[0]=0;
                for(int i=0;i<m;++i){
                    int val=l==0?matrix[i][r]:(matrix[i][r]-matrix[i][l-1]);
                    //三目操作符前后本质一样只不过是为了防止0下标越界
                    sum[i+1]=sum[i]+val;
                    //每行的前缀和求出来之后我们求范围的前缀和
                }
                ans=max(ans,maxsum(m,sum,k));
                //maxsum就是我们的查找操作下面具体解释。
            }
        }

        现在我们得到了在l,r这个范围内的行前缀和，并决定去查找答案。maxsum中有三个参数：行数m，前缀和数组sum,和不能超过的最大数字k。那么在该范围内的部分和该怎么求呢？我们假定两行 i , j(j > i)，那么这个范围和就是sum[j] -sum[i],当然这样解释肯定是不能够很好的理解的，看下面的图（依然画的不好。。。）。

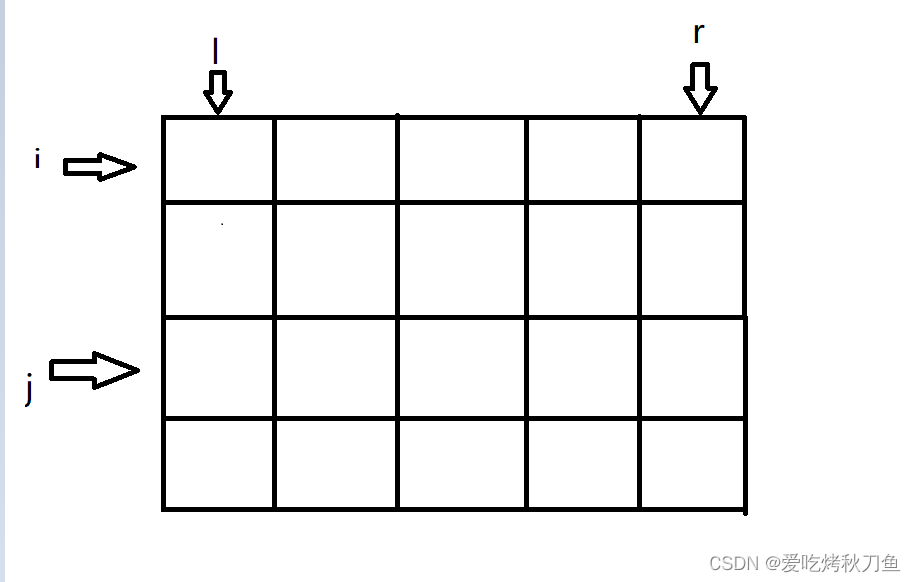
        我们的sum数组就是从[0,l],到[j,r]每行的前缀和，其中每个元素代表的是从第0行到第i行每行的前缀和。那么在这个范围内某个范围的和就是sum[j]-sum[i],现在我们想要寻找一个范围使得这个范围内的和小于等于k,也就是sum[j]-sum[i]<=k。

        现在我们固定其中一行j，就得到了一个不等式：sum[i]>=sum[j]-k,再看题目要求的结果是不超过k的最大范围和，也就是某个最小值的最大值，于是很自然的想到了二分查找。
        这里我们固定一个较大行j,然后去在一个有序的集合中进行二分查找，找出集合中大于等于sum[j]-k的最小值，因为sum[i]是要做减数的要尽量的小这样最后的结果才能尽量大，这里就可以利用set来进行这个操作，set中有一个函数lower_bound是在set中查找大于等于给定值的最小元素，返回值是一个迭代器，找不到返回的是set.end()。

	int maxsum(int m,int* sum,int k){
        set<int> s;
        s.insert(sum[0]);
        int ans=INT_MIN;
        for(int i=1;i<=m;++i){
            auto it=s.lower_bound(sum[i]-k);
            if(s.end()!=it){
                ans=max(ans,sum[i]-*it);
            }
            s.insert(sum[i]);
        }
        return ans;
    }

        接下来要做的就是维护我们的ans，每个范围查找出一个最优的答案之后我们选取最大的答案。另外就是答案的最大值一定是不超过k的最大范围和，所以很容易想到答案最大为k，于是在得到了某个答案是k的时候直接跳出循环即可。

class Solution {
    #define maxn 110
    int maxsum(int m,int* sum,int k){
        set<int> s;
        s.insert(sum[0]);
        int ans=INT_MIN;
        for(int i=1;i<=m;++i){
            auto it=s.lower_bound(sum[i]-k);
            if(s.end()!=it){
                ans=max(ans,sum[i]-*it);
            }
            s.insert(sum[i]);
        }
        return ans;
    }
public:
    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
        int l,r;
        int ans=INT_MIN;
        int m=matrix.size();
        int n=matrix[0].size();
        for(int i=0;i<m;++i){
            for(int j=1;j<n;++j){
                matrix[i][j]+=matrix[i][j-1];
            }
        }
        for(l=0;l<n;++l){
            for(r=l;r<n;++r){
                int sum[maxn];
                sum[0]=0;
                for(int i=0;i<m;++i){
                    int val=l==0?matrix[i][r]:(matrix[i][r]-matrix[i][l-1]);
                    sum[i+1]=sum[i]+val;
                }
                ans=max(ans,maxsum(m,sum,k));
                if(ans==k){
                	break;
            	}
            }
            if(ans==k){
                break;
            }
        }
        return ans;
    }
};