每日刷题计划Day9-树

题源：LeetCode

226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

方法：递归

这是一道很经典的二叉树问题。显然，我们从根节点开始，递归地对树进行遍历，并从叶子节点先开始翻转。如果当前遍历到的节点 root 的左右两棵子树都已经翻转，那么我们只需要交换两棵子树的位置，即可完成以 root 为根节点的整棵子树的翻转。

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr;
        }
        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);
        root->left = right;
        root->right = left;
        return root;
    }
};

复杂度分析

时间复杂度：O(N)，其中 NN 为二叉树节点的数目。我们会遍历二叉树中的每一个节点，对每个节点而言，我们在常数时间内交换其两棵子树。

空间复杂度：O(N)。使用的空间由递归栈的深度决定，它等于当前节点在二叉树中的高度。在平均情况下，二叉树的高度与节点个数为对数关系，即 O(logN)。而在最坏情况下，树形成链状，空间复杂度为 O(N)。

103. 二叉树的锯齿形层序遍历

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

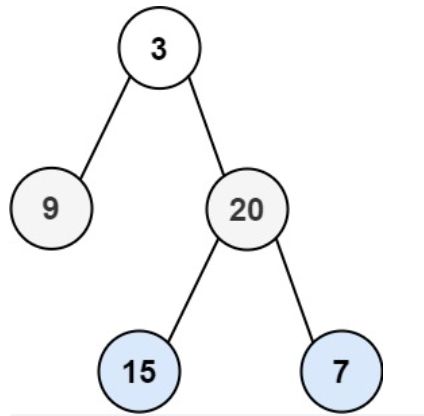
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        vector<vector<int> > ans;
        if(!root) return ans;

        queue<TreeNode*> nodeQueue;
        nodeQueue.push(root);
        bool isOrderLeft = true;

        while(!nodeQueue.empty()){
            deque<int> levelList;//双端队列，存结果
            int size = nodeQueue.size();
            for(int i = 0; i < size; i++){//树的一层
                auto node = nodeQueue.front();
                nodeQueue.pop();//出队列
                if(isOrderLeft){
                    levelList.push_back(node->val);
                } else {
                    levelList.push_front(node->val);
                }

                if(node -> left)  nodeQueue.push(node -> left);
                if(node -> right)  nodeQueue.push(node -> right);
            }
            ans.emplace_back(vector<int>{levelList.begin(), levelList.end()});
            isOrderLeft = !isOrderLeft;
        }
        return ans;
    }
};

543. 二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

思路：其实就是求节点的左右路径之和减一，取一个最大值。

class Solution {
private:    int ans = 0;
public:
    int depth(TreeNode* root){
        if(root == NULL){
            return 0;
        }
        int L = depth(root -> left);
        int R = depth(root -> right);
        ans = max(ans, L + R);
        return max(L, R)+1;
    }
    int diameterOfBinaryTree(TreeNode* root) {
        depth(root);
        return ans;
    }
};

101. 对称二叉树

给你一个二叉树的根节点root，检查它是否轴对称。

输入：root = [1,2,2,3,4,4,3]
输出：true

方法一：递归
通过「同步移动」两个指针的方法来遍历这棵树，p 指针和 q 指针一开始都指向这棵树的根，随后 p 右移时，q 左移，p 左移时，q 右移。每次检查当前 p 和 q 节点的值是否相等，如果相等再判断左右子树是否对称。

class Solution {
public:
    bool check(TreeNode *p, TreeNode *q) {
        if (!p && !q) return true;
        if (!p || !q) return false; //p指向空且q指向空的情况被上面一行挡住了
        return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);
    }

    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};

复杂度分析
假设树上一共 n 个节点。

• 时间复杂度：这里遍历了这棵树，渐进时间复杂度为 O(n)。
• 空间复杂度：这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过 n，故渐进空间复杂度为 O(n)。

方法二：迭代
把递归程序改写成迭代程序的常用方法：引入队列。

初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值（队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像），然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。

class Solution {
public:
    bool check(TreeNode *u, TreeNode *v) {
        queue <TreeNode*> q;
        q.push(u); q.push(v);
        while (!q.empty()) {
            u = q.front(); q.pop();
            v = q.front(); q.pop();
            if (!u && !v) continue;
            if ((!u || !v) || (u->val != v->val)) return false;

            q.push(u->left); 
            q.push(v->right);

            q.push(u->right); 
            q.push(v->left);
        }
        return true;
    }

    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。
示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3。

简单dfs：

class Solution {
private:    int ans =0;
public:
    int dfs(TreeNode* root){
        //边界
        if(!root) return 0;
        int l(0), r(0);
        l = dfs(root->left);
        r = dfs(root->right);
        int  res = max(l, r);
        ans = max(ans, res+1);
        return res + 1;
    }
    int maxDepth(TreeNode* root) {
        dfs(root);
        return ans;
    }
};

剑指 Offer 26. 树的子结构

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

解题思路：
若树 B 是树 A 的子结构，则子结构的根节点可能为树 A 的任意一个节点。因此，判断树 B 是否是树 A 的子结构，需完成以下两步工作：

1.先序遍历树 A 中的每个节点 ；（对应函数 isSubStructure(A, B)）
2.判断树 A中以某节点为根节点的子树 是否包含树 B 。（对应函数 judge(A, B)）

class Solution {
public:
    bool judge(TreeNode* A, TreeNode* B){
    /*
    终止条件：
		当节点 B 为空：说明树 B 已匹配完成（越过叶子节点），因此返回 true ；
		当节点 A 为空：说明已经越过树 A 叶子节点，即匹配失败，返回 false ；
		当节点 A 和 B 的值不同：说明匹配失败，返回 false 。
    */
        if(!B) return true;
        if(!A || A->val != B->val) return false;
     /*
     返回值：
     	判断A和B的左子节点是否相等，判断A和B的右子节点是否相等。
     */
        return judge(A->left, B->left) && judge(A->right, B->right);
    }
    bool isSubStructure(TreeNode* A, TreeNode* B) {
   	/*
   	特例处理：当树A为空或树B为空时，直接返回false；
   	返回值：若树B是树A的子结构，则必满足以下三种情况之一，因此用 或 连接：
   		1.以节点A为根节点的子树，包含树B，对应judge(A, B);
   		2.树B是树A左子树的子结构，对应isSubStructure(A->left, B)；
   		3.树B是树A右子树的子结构，对应isSubStructure(A->right, B)；
   	*/
       return (A && B) && (judge(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B));
    }
};

106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树 。

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

提示：

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

方法一：递归
思路：

• 后序遍历的数组最后一个元素代表的即为根节点。可以利用已知的根节点信息在中序遍历的数组中找到根节点所在的下标，然后根据其将中序遍历的数组分成左右两部分，左边部分即左子树，右边部分为右子树，针对每个部分可以用同样的方法继续递归下去构造。
• 为了高效查找根节点元素在中序遍历数组中的下标，我们选择创建哈希表来存储中序序列，即建立一个（元素，下标）键值对的哈希表。
• 定义递归函数 helper(inLeft, inRight) 表示当前递归到中序序列中当前子树的左右边界，递归入口为helper(0, n - 1) ：

  • 如果 inLeft > inRight，说明子树为空，返回空节点。

  • 选择后序遍历的最后一个节点作为根节点。

  • 利用哈希表 O(1) 查询当根节点在中序遍历中下标为 index。从 inLeft 到 index - 1 属于左子树，从 index + 1 到 inRight 属于右子树。

  • 根据后序遍历逻辑，递归创建右子树 helper(index + 1, inRight) 和左子树 helper(inLeft, index - 1)。注意这里有需要先创建右子树，再创建左子树的依赖关系。可以理解为在后序遍历的数组中整个数组是先存储左子树的节点，再存储右子树的节点，最后存储根节点，如果按每次选择「后序遍历的最后一个节点」为根节点，则先被构造出来的应该为右子树。

  • 返回根节点 root。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    int postIdx;
    unordered_map<int, int> idxMap;
public:
    TreeNode* helper(int inLeft, int inRight,vector<int>& inorder, vector<int>& postorder){
        //如果这里没有节点构造二叉树了，就结束。
        if(inLeft > inRight) return nullptr;

        //选择postIdx位置的元素作为当前子树根节点
        int rootVal = postorder[postIdx];
        TreeNode* root = new TreeNode(rootVal);

        //根据root所在位置分成左右两棵子树
        int index = idxMap[rootVal];//值为rootVal的下标

        postIdx--;

        /*  
            注意这里有需要先创建右子树，再创建左子树的依赖关系。
            可以理解为在后序遍历的数组中整个数组是先存储左子树的节点，再存储右子树的节点，最后存储根节点。
            如果按每次选择「后序遍历的最后一个节点」为根节点，则先被构造出来的应该为右子树。
        */
        //构造右子树
        root->right = helper(index + 1, inRight, inorder, postorder);
        //构造左子树
        root->left = helper(inLeft, index - 1, inorder, postorder);

        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        postIdx = (int)postorder.size() - 1;//后序遍历的最后一个元素
        
        //建立<元素，下标>键值对的哈希表
        int idx = 0;
        for(auto& val : inorder){
            idxMap[val] = idx++;
        }

        return helper(0, (int)inorder.size() - 1, inorder, postorder);
    }
};

337. 打家劫舍 III

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

示例 1:

输入: root = [3,2,3,null,3,null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

示例 2:

输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

坑：不是简单的层序遍历各层求解和， 例如[2,1,3,null,4] 这样的测试用例，第一层右边的节点和第二层左边的节点也可以求和。

简化问题：一棵二叉树，树上的每个点都有对应的权值，每个点有两种状态（选中和不选中），问在不能同时选中有父子关系的点的情况下，能选中的点的最大权值和是多少。

我们可以用 f(o)表示选择 o 节点的情况下，o 节点的子树上被选择的节点的最大权值和；g(o)表示不选择 o 节点的情况下，o 节点的子树上被选择的节点的最大权值和；l 和 r 代表 o 的左右孩子。
- 当 o 被选中时，o 的左右孩子都不能被选中，故 o 被选中情况下子树上被选中点的最大权值和为 l 和 r 不被选中的最大权值和相加，即 f(o) = g(l) + g®。
- 当 o 不被选中时，o 的左右孩子可以被选中，也可以不被选中。对于 o 的某个具体的孩子 x，它对 o 的贡献是 x 被选中和不被选中情况下权值和的较大值。故 g(o) = max{f(l), g(l)} + max{f®, g®}。

至此，我们可以用哈希表来存 f 和 g 的函数值，用深度优先搜索的办法后序遍历这棵二叉树，我们就可以得到每一个节点的 f 和 g。根节点的 f 和 g 的最大值就是我们要找的答案。

class Solution {
public:
    unordered_map <TreeNode*, int> f, g;

    void dfs(TreeNode* node) {
        if (!node) {
            return;
        }
        dfs(node->left);
        dfs(node->right);
        f[node] = node->val + g[node->left] + g[node->right];
        g[node] = max(f[node->left], g[node->left]) + max(f[node->right], g[node->right]);
    }

    int rob(TreeNode* root) {
        dfs(root);
        return max(f[root], g[root]);
    }
};

假设二叉树的节点个数为 n。
，以上的算法对二叉树做了一次后序遍历，时间复杂度是 O(n)；由于递归会使用到栈空间，空间代价是 O(n)，哈希表的空间代价也是 O(n)，故空间复杂度也是 O(n)。

我们可以做一个小优化，我们发现无论是 f(o) 还是 g(o)，他们最终的值只和 f(l)、g(l)、f®、g® 有关，所以对于每个节点，我们只关心它的孩子节点们的 f 和 g 是多少。我们可以设计一个结构，表示某个节点的 f 和 g 值，在每次递归返回的时候，都把这个点对应的 f 和 g 返回给上一级调用，这样可以省去哈希表的空间。

struct SubtreeStatus {
    int selected;
    int notSelected;
};

class Solution {
public:
    SubtreeStatus dfs(TreeNode* node) {
        if (!node) {
            return {0, 0};
        }
        auto l = dfs(node->left);
        auto r = dfs(node->right);
        int selected = node->val + l.notSelected + r.notSelected;
        int notSelected = max(l.selected, l.notSelected) + max(r.selected, r.notSelected);
        return {selected, notSelected};
    }

    int rob(TreeNode* root) {
        auto rootStatus = dfs(root);
        return max(rootStatus.selected, rootStatus.notSelected);
    }
};

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 ：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

题解来自：无明逆流

• 最近公共祖先的情况无外乎三种情况，解答此题最好分别画出三种情况的草图，问题便迎刃而解
○ 树形一：root为p,q中的一个，这时公共祖先为root
○ 树形二：p,q分别在root的左右子树上（p在左子树，q在右子树；还是p在右子树，q在左子树的情况都统一放在一起考虑）这时满足p,q的最近公共祖先的结点也只有root本身
○ 树形三：p和q同时在root的左子树；或者p,q同时在root的右子树，这时确定最近公共祖先需要遍历子树来进行递归求解。

• 清楚了这些，开始编写程序，首先要明确递归的方式，需要采用类似后序遍历的方式，先遍历左，右子树得到结果，再根据结果判断出当前树形属于前面三种讨论的哪一种，再返回相应的答案。
• 接下来开始着手实现细节：
○ 明确递归边界：root为空（此时为空树），则直接返回NULL，不存在公共祖先；root为p或q中的一个，则直接返回root;
这两种情况都是不需要通过递归直接能得出答案的，故直接终止递归返回即可
○ 用left_have，right_have分别去接收遍历左右子树得到的结点（这里递归返回值是结点指针）
○ 如果left_have和right_have均不为空，注意此时left_have,right_have并不是理解为子树上p,q的最近公共祖先，而是结点p或q自身的指针，这时说明p,q分别存在于root根结点的左右两端，是符合树形二的情况，直接返回root。
○ 如果left_have，right_have中有一个为空，那么通过树形的分析，必然属于树形三;
因为是递归，使用函数后可认为左右子树已经算出结果。此时left_have,right_have代表的含义就是子树上层层向上返回的最近公共祖先，最开始的调用层拿到这个结果后直接返回不空的那一个，即是答案。

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == NULL) return NULL;           //递归边界
        if(root == p || root == q) return root;

        //分解为求左子树的子问题和右子树的子问题,注意是后序遍历
        TreeNode* left_have = lowestCommonAncestor(root->left,p,q);     
        TreeNode* right_have = lowestCommonAncestor(root->right,p,q);   
        if(left_have && right_have) return root;        //左右子树都有则返回root
        else return left_have ? left_have : right_have;     //如果左右子树中有一个子问题没得到结果，则返回得到结果的子问题.
}