Task6-7

Task6

批量归一化

BatchNormalization想要解决的问题：Internal Covariate Shift

作者：Juliuszh
链接：https://zhuanlan.zhihu.com/p/33173246
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

1.2 深度学习中的 Internal Covariate Shift

深度神经网络模型的训练为什么会很困难？其中一个重要的原因是，深度神经网络涉及到很多层的叠加，而每一层的参数更新会导致上层的输入数据分布发生变化，通过层层叠加，高层的输入分布变化会非常剧烈，这就使得高层需要不断去重新适应底层的参数更新。为了训好模型，我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。

Google 将这一现象总结为 Internal Covariate Shift，简称 ICS. 什么是 ICS 呢？

@魏秀参

在一个回答中做出了一个很好的解释：

大家都知道在统计机器学习中的一个经典假设是“源空间（source domain）和目标空间（target domain）的数据分布（distribution）是一致的”。如果不一致，那么就出现了新的机器学习问题，如 transfer learning / domain adaptation 等。而 covariate shift 就是分布不一致假设之下的一个分支问题，它是指源空间和目标空间的条件概率是一致的，但是其边缘概率不同，即：对所有[图片上传失败...(image-a57c44-1582635612735)]

但是[图片上传失败...(image-5235d6-1582635612735)]大家细想便会发现，的确，对于神经网络的各层输出，由于它们经过了层内操作作用，其分布显然与各层对应的输入信号分布不同，而且差异会随着网络深度增大而增大，可是它们所能“指示”的样本标记（label）仍然是不变的，这便符合了covariate shift的定义。由于是对层间信号的分析，也即是“internal”的来由。

1.3 ICS 会导致什么问题？

简而言之，每个神经元的输入数据不再是“独立同分布”。

其一，上层参数需要不断适应新的输入数据分布，降低学习速度。

其二，下层输入的变化可能趋向于变大或者变小，导致上层落入饱和区，使得学习过早停止。

其三，每层的更新都会影响到其它层，因此每层的参数更新策略需要尽可能的谨慎。

[图片上传失败...(image-4e9d98-1582635612735)]

最后scale and shift中分别称为缩放系数，平移系数。

作用：为了保证模型的表达能力不因为规范化而下降。

批量归一化层在仿射变换之后，激活函数之前。

其他归一化方法

Layer Normalization

Instance Normalization

Group Normalization

FRN（Filter Response Normalization）

残差网络

动机：网络退化

在神经网络可以收敛的前提下，随着网络深度增加，网络的表现先是逐渐增加至饱和，然后迅速下降[1]。

需要注意，网络退化问题不是过拟合导致的，即便在模型训练过程中，同样的训练轮次下，退化的网络也比稍浅层的网络的训练错误更高，如下图[1]所示。

[模型退化：深层模型反而取得更低的训练和测试误差]

这一点并不符合常理：如果存在某个层的网络是当前最优的网络，那么可以构造一个更深的网络，其最后几层仅是该网络第层输出的恒等映射(Identity Mapping)，就可以取得与一致的结果；也许还不是所谓“最佳层数”，那么更深的网络就可以取得更好的结果。总而言之，与浅层网络相比，更深的网络的表现不应该更差。因此，一个合理的猜测就是，对神经网络来说，恒等映射并不容易拟合。

作者：LinT
链接：https://zhuanlan.zhihu.com/p/80226180
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

残差块

image.png

image.png

在前向传播时，输入信号可以从任意低层直接传播到高层。由于包含了一个天然的恒等映射，一定程度上可以解决网络退化问题。

网络结构

img

img

稠密网络

img

DenseNet：比ResNet更优的CNN模型 - 小小将的文章 - 知乎 https://zhuanlan.zhihu.com/p/37189203

凸优化

凸函数的定义：

Jensen不等式：

凸函数的期望大于等于期望的凸函数

性质

1. 无局部最小值

梯度下降

牛顿法

梯度下降法、牛顿法和拟牛顿法 - Eureka的文章 - 知乎 https://zhuanlan.zhihu.com/p/37524275

image.png

红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

image.png

动态学习率

image.png

先大后小

Task7

优化算法

一般来说，ill-conditioned是指问题的条件数（condition number）非常大，从而比较难以优化，或者说需要更多迭代次数来达到同样精度。直观上来讲，条件数是：函数梯度最大变化速度 / 梯度最小变化速度（对于二阶可导函数，条件数的严格定义是：Hessian矩阵最大特征值的上界 / 最小特征值的下界）。

用最简单的话来解释就是，问题条件数大意味着目标函数在有的地方（或有的方向）变化很快、有的地方很慢，比较不规律，从而很难用当前的局部信息（也就是梯度）去比较准确地预测最优点所在的位置，只能一步步缓慢的逼近最优点，从而优化时需要更多的迭代次数。

作者：Martin Tan
链接：https://www.zhihu.com/question/56977045/answer/151137770
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

img

Solution to ill-condition

• Preconditioning gradient vector: applied in Adam, RMSProp, AdaGrad, Adelta, KFC, Natural gradient and other secord-order optimization algorithms.
• Averaging history gradient: like momentum, which allows larger learning rates to accelerate convergence; applied in Adam, RMSProp, SGD momentum.

Momentum动量

设时间步的自变量为，学习率为。 在时间步0，动量法创建速度变量，并将其元素初始化成0。在时间步，动量法对每次迭代的步骤做如下修改：

其中，动量超参数 满足。当时，动量法等价于小批量随机梯度下降。

或：

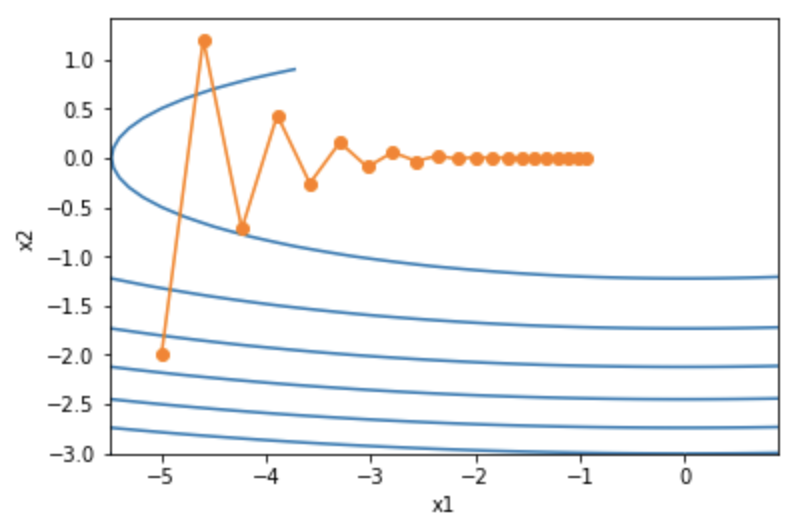
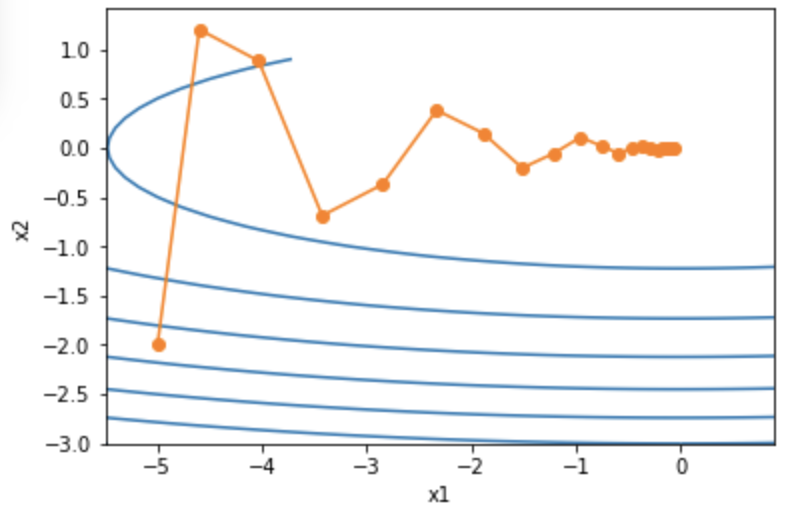
AdaGrad

初始化为0, 为按元素平方

1. 较大时，学习率下降得快

2. 较小时，学习率下降得慢

3. 若前期下降过快则后期学习率后期过小

   

RMSProp

指数移动平均调整学习率

可以看作是最近个时间步的小批量随机梯度平方项的加权平均。如此一来，自变量每个元素的学习率在迭代过程中就不再一直降低（或不变）。

[图片上传失败...(image-49a745-1582635612735)]

AdaDelta

在RMSProp的基础上，维护一个额外的状态变量代替学习率

在pytorch中的参数名是rho -

Adam

Adaptive Moment Estimation

本质上是带有动量项的RMSprop，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率