谱方法学习笔记-上(超详细)
谱方法学习笔记
谱方法学习笔记-下(超详细)
声明:鉴于CSDN使用 K a T e X KaTeX KaTeX 渲染公式, KaTeX \KaTeX KATEX 与 L a T e X LaTeX LaTeX 不同,不支持直接的交叉引用命令,如\label和\eqref。 KaTeX \KaTeX KATEX专注于数学公式的呈现,而不提供完整的文档生成功能。因此,为了保证显示正常,本文中所有公式均已删除编号和交叉引用。由此可能导致一些可读性上的不便,请读者谅解。
文章目录
- 谱方法学习笔记
-
- 傅立叶谱方法
-
- 求导与傅里叶谱方法
- 傅立叶谱方法的步聚
- 傅里叶谱方法求解基本偏微分方程---一维波动方程
- 傅里叶谱方法求解基本偏微分方程—二维波动方程
傅立叶谱方法
对于在 ( − ∞ , ∞ ) (-\infty, \infty) (−∞,∞) 有定义且绝对可积、并在任一有限区间上满足狄利克莱条件的函数 u ( x ) u(x) u(x), 傅里叶变换(Fourier transform)及其逆变换(inverse Fourier transform) 定义为:
u ^ ( k ) = ∫ − ∞ ∞ u ( x ) e − i k x d x \hat{u}(k)=\int_{-\infty}^{\infty} u(x) \mathrm{e}^{-\mathrm{i} k x} \mathrm{~d} x% \label{3-1} u^(k)=∫−∞∞u(x)e−ikx dx
u ( x ) = 1 2 π ∫ − ∞ ∞ u ^ ( k ) e i k x d k u(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \hat{u}(k) \mathrm{e}^{\mathrm{i} k x} \mathrm{~d} k % \label{3-2} u(x)=2π1∫−∞∞u^(k)eikx dk
上述定义式给出了一个傅里叶变换对 (Fourier transform pair), 本专栏中将它们记为 u ^ ( k ) = F [ u ( x ) ] \hat{u}(k)=F[u(x)] u^(k)=F[u(x)] 和 u ( x ) = F − 1 [ u ^ ( k ) ] u(x)=F^{-1}[\hat{u}(k)] u(x)=F−1[u^(k)] .实际上, 傅里叶变换对的定义并不是唯一的, 两个定义式中的系数可以随意修改, 只要它们的积为 1 / 2 π 1 / 2 \pi 1/2π 即可.此外, 定义式中的 e − i k x \mathrm{e}^{-\mathrm{i} k x} e−ikx 和 e i k x \mathrm{e}^{\mathrm{i} k x} eikx (称为积分变换的核) 也可以互换.容易知道, u ( x ) u(x) u(x) 先后经过傅里叶变换及其逆变换仍将得到它本身, 即: u ( x ) = F − 1 { F [ u ( x ) ] } u(x)=F^{-1}\{F[u(x)]\} u(x)=F−1{F[u(x)]} .
通常来讲, 若不对 “傅里叶变换” 加任何限定, 那么它指的就是连续傅里叶变换, 也 就是针对定义在无限区间内的连续函数 u ( x ) u(x) u(x) 的傅里叶变换, 这是在理想条件下的数学定义. 在实际应用中, 尤其是计算机的信号采样、信号处理当中, 信号是离散的、有限的, 离散傅里叶变换(discrete Fourier transform) 就是针对这一情况提出的.在 Matlab 中, 对于序列 u 1 , … , u j , … , u N u_1, \ldots, u_j, \ldots, u_N u1,…,uj,…,uN 的离散傅里叶变换及逆变换定义为:
u ^ k = ∑ j = 1 N u j e − 2 π ( j − 1 ) ( k − 1 ) i N , k = 1 , … , N \hat{u}_k=\sum_{j=1}^N u_j \mathrm{e}^{\frac{-2 \pi(j-1)(k-1) \mathrm{i}}{N}}, \quad k=1, \ldots, N % \label{3-4} u^k=j=1∑NujeN−2π(j−1)(k−1)i,k=1,…,N
u j = 1 N ∑ k = 1 N u ^ k e 2 π ( j − 1 ) ( k − 1 ) i N , j = 1 , … , N u_j=\frac{1}{N} \sum_{k=1}^N \hat{u}_k \mathrm{e}^{\frac{2 \pi(j-1)(k-1) \mathrm{i}}{N}}, \quad j=1, \ldots, N% \label{3-5} uj=N1k=1∑Nu^keN2π(j−1)(k−1)i,j=1,…,N
同样, 上述定义中的归一化系数也可以有其他选择, 但它们的乘积必须为 1 / N 1 / N 1/N .如果将序列 u 1 , … , u j , … , u N u_1, \ldots, u_j, \ldots, u_N u1,…,uj,…,uN 看作等间隔空间(时间)点上的信号幅度值, 那么经过离散傅里叶变换得到的序列 u ^ 1 , … , u ^ k , … , u ^ N \hat{u}_1, \ldots, \hat{u}_k, \ldots, \hat{u}_N u^1,…,u^k,…,u^N 就是其相应的频谱信息.通过定义式 % \eqref{3-4} 和 % \eqref{3-5} 容易得到 u ^ k = u ^ k + N \hat{u}_k=\hat{u}_{k+N} u^k=u^k+N 和 u j = u j + N u_j=u_{j+N} uj=uj+N, 这就是说, 离散傅里叶变换已经隐含了周期性边界条件.
在 Matlab 中,fft 和 ifft 函数实现基于快速傅里叶变换算法的一维离散傅里叶变换及逆变换。fft 函数的一般调用语法为:
fft(u)
若u为一向量,则 fft 返回其离散傅里叶变换的结果。若 u为一矩阵,则 fft 返回矩阵中每一列的离散傅里叶变换。若要计算矩阵 u 中每一行的离散傅里叶变换,只需调用 fft(u,[],2)即可,它速度比 fft(u.').'更快一些。ifft 函数的调用语法与 fft 函数完全一样。
若输入 fft 函数的空域信号序列 u 1 , . . . , u j , . . . , u N u_1,...,u_j,...,u_N u1,...,uj,...,uN 在 x x x 轴上的坐标间隔是 L / N L/N L/N , 相应的横坐标 x x x 可认为是:
− L / 2 , − L / 2 + L / N , … , L / 2 − 2 L / N , L / 2 − L / N -L/2,-L/2+L/N,\ldots,L/2-2L/N,L/2-L/N −L/2,−L/2+L/N,…,L/2−2L/N,L/2−L/N
注意,fft 函数输出的序列 u ^ 1 , . . . , u ^ k , . . . , u ^ N \hat{u}_1,...,\hat{u}_k,...,\hat{u}_N u^1,...,u^k,...,u^N 所对应的频率并不是按照从小到大的顺序排列的,而是非负频率对应于前半部分序列,负频率对应于后半部分序列,即:
0 , 2 π / L , 4 π / L , … , ( N − 4 ) π / L , ( N − 2 ) π / L , − N π / L , − ( N − 2 ) π / L , … , − 4 π / L , − 2 π / L 0,2\pi/L,4\pi/L,\ldots,(N-4)\pi/L,(N-2)\pi/L,-N\pi/L,-(N-2)\pi/L,\ldots,-4\pi/L,-2\pi/L 0,2π/L,4π/L,…,(N−4)π/L,(N−2)π/L,−Nπ/L,−(N−2)π/L,…,−4π/L,−2π/L
因此 Matlab 提供了 fftshift 函数,用于调整 fft 输出序列的顺序。也就是说,fftshift(fft(u)) 所对应的频率才是按照递增顺序排列的:
− N π / L , − ( N − 2 ) π / L , … , − 2 π / L , 0 , 2 π / L , … , ( N − 4 ) π / L , ( N − 2 ) π / L -N\pi/L,-(N-2)\pi/L,\ldots,-2\pi/L,0,2\pi/L,\ldots,(N-4)\pi/L,(N-2)\pi/L −Nπ/L,−(N−2)π/L,…,−2π/L,0,2π/L,…,(N−4)π/L,(N−2)π/L
空域坐标与频域坐标的关系如下表所示,不难发现,空域上的两点间隔和频域区间长度成反比,乘积为 2 π 2\pi 2π, 频域上的两点间隔和空域区间长度的关系亦如此。
| 两点间隔 | 区间长度 | |
|---|---|---|
| 空域坐标 | L / N L / N L/N | L L L |
| 频域坐标 | 2 π / L 2 \pi / L 2π/L | 2 π N / L 2 \pi N / L 2πN/L |
此外还有 ifftshift 函数用于进行与 fftshift 函数相反的操作。实际上,fftshift 函数的作用仅是让 fft 的输出结果变得更易于观察,若还需要用 ifft 函数将频谱信息还原回空域信号,就必须在使用 fftshift 之后再用 ifftshift 函数将序列的顺序恢复,否则得不到正确结果。如果不是为了分析频谱信息,而是用下文即将介绍的傅里叶谱方法处理导数和微分问题,则大可不必使用 fftshift 和 ifftshift 函数调整序列的顺序,以减少代码冗余、 节约时间。
基于快速傅里叶变换算法的二维离散傅里叶变换及逆变换由 fft2、ifft2 函数实现,一般调用语法为:
fft2(u)
它返回矩阵 u 的二维傅里叶变换,等效于 fft(fft(u),[],2)。ifft2 与 fft2 的调用语法一样,就不再赘述。
fftshift 函数的调用语法为:
fftshift(u)
若u为一向量,它将 u 左右两半互换并返回。若 u 为一矩阵,则它将 u 的第 1、3 象限互换以及第 2、4 象限互换并返回。此外,若要互换矩阵 u 的上下两半,可以调用 fftshift(u,1)。要互换矩阵 u 的左右两半,只需调用 fftshift(u,2)。ifftshift 函数与 fftshift 函数功能完全相反, 调用语法相同,这里不再重复。
求导与傅里叶谱方法
对于 F [ u ′ ( x ) ] F\left[u^{\prime}(x)\right] F[u′(x)], 由傅里叶变换的定义和分部积分法, 得到:
F [ u ′ ( x ) ] = ∫ − ∞ ∞ u ′ ( x ) e − i k x d x = u ( x ) e − i k x ∣ − ∞ ∞ − ∫ − ∞ ∞ u ( x ) ( − i k ) e − i k x d x F\left[u^{\prime}(x)\right]=\int_{-\infty}^{\infty} u^{\prime}(x) \mathrm{e}^{-\mathrm{i} k x} \mathrm{~d} x=\left.u(x) \mathrm{e}^{-\mathrm{i} k x}\right|_{-\infty} ^{\infty}-\int_{-\infty}^{\infty} u(x)(-\mathrm{i} k) \mathrm{e}^{-\mathrm{i} k x} \mathrm{~d} x% \label{3-7} F[u′(x)]=∫−∞∞u′(x)e−ikx dx=u(x)e−ikx −∞∞−∫−∞∞u(x)(−ik)e−ikx dx
当 ∣ x ∣ → ∞ \mid x\mid \rightarrow \infty ∣x∣→∞ 时, u ( x ) → 0 u(x) \rightarrow 0 u(x)→0, 则:
F [ u ′ ( x ) ] = i k ∫ − ∞ ∞ u ( x ) e − i k x d x = i k F [ u ( x ) ] F\left[u^{\prime}(x)\right]=\mathrm{i} k \int_{-\infty}^{\infty} u(x) \mathrm{e}^{-\mathrm{i} k x} \mathrm{~d} x=\mathrm{i} k F[u(x)]% \label{3-8} F[u′(x)]=ik∫−∞∞u(x)e−ikx dx=ikF[u(x)]
类似地, 可以得到:
F [ u ( n ) ( x ) ] = ( i k ) n F [ u ( x ) ] F\left[u^{(n)}(x)\right]=(\mathrm{i} k)^n F[u(x)]% \label{3-9} F[u(n)(x)]=(ik)nF[u(x)]
其中 u ( n ) ( x ) u^{(n)}(x) u(n)(x) 代表 u ( x ) u(x) u(x) 的 n n n 阶导数.上式的意义在于:函数的求导运算在傅里叶变换的作用下, 可转化为相对简单的代数运算, 即: u ( n ) ( x ) = F − 1 { ( i k ) n F [ u ( x ) ] } u^{(n)}(x)=F^{-1}\left\{(\mathrm{i} k)^n F[u(x)]\right\} u(n)(x)=F−1{(ik)nF[u(x)]} .正是基于此原理, 傅里叶谱方法 (Fourier spectral method) 利用傅里叶变换将偏微分方程中空域 (space domain)或时域(time domain)上的求导运算简化为频域 ( spectral domain) 上的代数运算, 求解后再通过傅里叶逆变换得到空域或时域上的结果.在代码层面上, Matlab 提供的快速傅里叶变换函数 fft、逆变换函数 ifft 以及强大的矩阵运算能力也为简洁、优雅地实现傅里叶谱方法奠定了基础.
如前所述,fft 输出结果在频域上的顺序是颠倒的,经过 fft 函数变换后的序列在 k k k 轴上所对应的坐标是:
0 , 2 π / L , 4 π / L , . . . , ( N − 4 ) π / L , ( N − 2 ) π / L , − N π / L , − ( N − 2 ) π / L , . . . , − 4 π / L , − 2 π / L 0,2\pi/L,4\pi/L,...,(N-4)\pi/L,(N-2)\pi/L,-N\pi/L,-(N-2)\pi/L,...,-4\pi/L,-2\pi/L 0,2π/L,4π/L,...,(N−4)π/L,(N−2)π/L,−Nπ/L,−(N−2)π/L,...,−4π/L,−2π/L
利用傅里叶谱方法求导时,在代码中通常使用顺序颠倒的频域坐标,以求序列 u 的一阶导数数值解为例:ifft(i*k.*fft(u))。其中,变量 k 是由 Matlab 语句 (2*pi/L)*[0:N/2-1 -N/2:-1] 生成的顺序颠倒的频域坐标,这样做是为了免去调用 fftshift 和 ifftshift 的步骤。
下面用实例说明傅里叶谱方法求 u ( x ) = e sin ( π x ) u(x)=\mathrm{e}^{\sin (\pi x)} u(x)=esin(πx) 的 1 、 2 、 3 1 、 2 、 3 1、2、3 阶导数的过程, 并与解析解
u ′ ( x ) = π cos ( π x ) e sin ( π x ) u^{\prime}(x)=\pi \cos (\pi x) \mathrm{e}^{\sin (\pi x)} u′(x)=πcos(πx)esin(πx)
u ′ ′ ( x ) = π 2 e sin ( π x ) [ cos 2 ( π x ) − sin ( π x ) ] u^{\prime \prime}(x)=\pi^2 \mathrm{e}^{\sin (\pi x)}\left[\cos ^2(\pi x)-\sin (\pi x)\right] u′′(x)=π2esin(πx)[cos2(πx)−sin(πx)]
u ′ ′ ′ ( x ) = π 3 e sin ( π x ) cos ( π x ) [ cos 2 ( π x ) − 3 sin ( π x ) − 1 ] u^{\prime \prime \prime}(x)=\pi^3 \mathrm{e}^{\sin (\pi x)} \cos (\pi x)\left[\cos ^2(\pi x)-3 \sin (\pi x)-1\right] u′′′(x)=π3esin(πx)cos(πx)[cos2(πx)−3sin(πx)−1]
相比较, 得到的最大误差分别在 1 0 − 14 、 1 0 − 13 、 1 0 − 11 10^{-14} 、 10^{-13} 、 10^{-11} 10−14、10−13、10−11 数量级, 如图所示.
 代码如下:
代码如下:
clear all; close all;
L=2; N=32;
x=L/N*[-N/2:N/2-1];
k=2*pi/L*[0:N/2-1 -N/2:-1];
u=exp(sin(pi*x)); ut=fft(u);
%导数的精确解
du_exact(:,1)=pi*cos(pi*x).*u;
du_exact(:,2)=pi^2*(cos(pi*x).^2-sin(pi*x)).*u;
du_exact(:,3)=pi^3*cos(pi*x).*(cos(pi*x).^2-3*sin(pi*x)-1).*u;
%谱方法求导
du_Fourier(:,1)=ifft(i*k.*ut);
du_Fourier(:,2)=ifft((i*k).^2.*ut);
du_Fourier(:,3)=ifft((i*k).^3.*ut);
error=max(abs(du_exact-du_Fourier));
%画图
labels={'u''(x)','u''''(x)','u''''''(x)'};
for n=1:4
subplot(2,2,n)
if n==1
plot(x,u,'k','LineWidth',1.5)
xlabel x, ylabel u(x), title('u(x)=e^{sin(\pix)}')
else
plot(x,du_exact(:,n-1),'k',x,du_Fourier(:,n-1),'.r' ...
,'MarkerSize',13,'LineWidth',1.5)
title(['Error_{max}=' num2str(error(n-1))])
xlabel x, ylabel(labels(n-1))
end
end
傅立叶谱方法的步聚
待求解的偏微分方程的普遍形式为:
∂ n u ∂ t n = L u + N ( u ) \frac{\partial^n u}{\partial t^n}=L u+N(u)% \label{3-11} ∂tn∂nu=Lu+N(u)
其中, u ( x , t ) u(x, t) u(x,t) 为 x 、 t x 、 t x、t 的函数, L L L 代表线性算符 (linear operator), N ( u ) N(u) N(u) 为非线性项 (nonlinear terms ).已知初始条件为 u ( x , t 0 ) u\left(x, t_0\right) u(x,t0), 在周期性边界条件下求某一时刻的 u ( x , t ) u(x, t) u(x,t) .对于这样的问题, 总是可以通过变量代换的办法将等号左边对 t t t 的 n n n 阶导数降为 1 阶, 所以下面以等号左边是 ∂ u / ∂ t \partial u / \partial t ∂u/∂t 的偏微分方程为例进行讨论, 这与式 % \eqref{3-11} 降阶后的偏微分方程组求解方法大同小异.
在 x x x 域上对以下方程做傅里叶变换:
∂ u ∂ t = L u + N ( u ) \frac{\partial u}{\partial t}=L u+N(u)% \label{3-12} ∂t∂u=Lu+N(u)
得到:
∂ u ^ ∂ t = α ( k ) u ^ + F [ N ( u ) ] \frac{\partial \hat{u}}{\partial t}=\alpha(k) \hat{u}+F[N(u)]% \label{3-13} ∂t∂u^=α(k)u^+F[N(u)]
其中, u ^ ( k , t ) \hat{u}(k, t) u^(k,t) 代表 u ( x , t ) u(x, t) u(x,t) 在 x x x 域上的傅里叶变换.为了展现对线性算符 L L L 及非线性项 N ( u ) N(u) N(u) 做傅里叶变换的细节, 这里以
L = a ⋅ ∂ 2 / ∂ x 2 + b ⋅ ∂ / ∂ x + c L=a \cdot \partial^2 / \partial x^2+b \cdot \partial / \partial x+c L=a⋅∂2/∂x2+b⋅∂/∂x+c
N ( u ) = u 3 + u 3 ⋅ ∂ 2 u / ∂ x 2 + f ( x ) ⋅ ∂ u / ∂ x N(u)=u^3+u^3 \cdot \partial^2 u / \partial x^2+f(x) \cdot \partial u / \partial x N(u)=u3+u3⋅∂2u/∂x2+f(x)⋅∂u/∂x
为例进行分析, a 、 b a 、 b a、b 和 c c c 分别为常数.
对线性部分, 有 F [ L u ] = [ a ( i k ) 2 + b ( i k ) + c ] u ^ , F[L u]=\left[a(\mathrm{i} k)^2+b(\mathrm{i} k)+c\right] \hat{u}, F[Lu]=[a(ik)2+b(ik)+c]u^, 则式 % \eqref{3-13} 中的 α ( k ) = a ( i k ) 2 + b ( i k ) + c = \alpha(k)=a(\mathrm{i} k)^2+b(\mathrm{i} k)+c= α(k)=a(ik)2+b(ik)+c= − a k 2 + i b k + c -a k^2+\mathrm{i} b k+c −ak2+ibk+c .
对非线性部分, 需要将 u 、 ∂ u / ∂ x u 、 \partial u / \partial x u、∂u/∂x 和 ∂ 2 u / ∂ x 2 \partial^2 u / \partial x^2 ∂2u/∂x2 写为 F − 1 [ u ^ ] 、 F − 1 [ i k u ^ ] F^{-1}[\hat{u}] 、 F^{-1}[\mathrm{i} k \hat{u}] F−1[u^]、F−1[iku^] 和 F − 1 [ ( i k ) 2 u ^ ] F^{-1}\left[(\mathrm{i} k)^2 \hat{u}\right] F−1[(ik)2u^], 则有
F [ N ( u ) ] = F [ u 3 + u 3 ⋅ ∂ 2 u / ∂ x 2 + f ( x ) ⋅ ∂ u / ∂ x ] = F { F − 1 [ u ^ ] 3 + F − 1 [ u ^ ] 3 ⋅ F − 1 [ ( i k ) 2 u ^ ] + f ( x ) ⋅ F − 1 [ i k u ^ ] } \begin{aligned} F[N(u)]&=F\left[u^3+u^3 \cdot \partial^2 u / \partial x^2+f(x) \cdot \partial u / \partial x\right]\\ &=F\left\{F^{-1}[\hat{u}]^3+F^{-1}[\hat{u}]^3 \cdot F^{-1}\left[(\mathrm{i} k)^2 \hat{u}\right]+f(x) \cdot F^{-1}[\mathrm{i} k \hat{u}]\right\}\end{aligned} F[N(u)]=F[u3+u3⋅∂2u/∂x2+f(x)⋅∂u/∂x]=F{F−1[u^]3+F−1[u^]3⋅F−1[(ik)2u^]+f(x)⋅F−1[iku^]}
这样, 式 % \eqref{3-12} 中 u ( x , t ) u(x, t) u(x,t) 对 x x x 的偏导数就都通过傅里叶变换及逆变换简化为式 % \eqref{3-13} 中 u ^ ( k , t ) \hat{u}(k, t) u^(k,t) 和 k k k 的代数运算了, 然后再将 u ^ \hat{u} u^ 和 k k k 离散化, 偏微分方程就简化成了常微分方程组.数值计算 ∂ u ^ ( k , t ) / ∂ t \partial \hat{u}(k, t) / \partial t ∂u^(k,t)/∂t 最直接的方法就是调用 Matlab 的 ode 系列函数, 优先选择 ode 45 函数, 最后用 ifft 函数将频域上的计算结果 u ^ ( k , t ) \hat{u}(k, t) u^(k,t) 变换回待求的 u ( x , t ) u(x, t) u(x,t) .
综上, 利用傅里叶谱方法数值计算偏微分方程 (组) 步骤如图(一维情况下的傅里叶谱方法计算过程)所示, 具体过程如下:
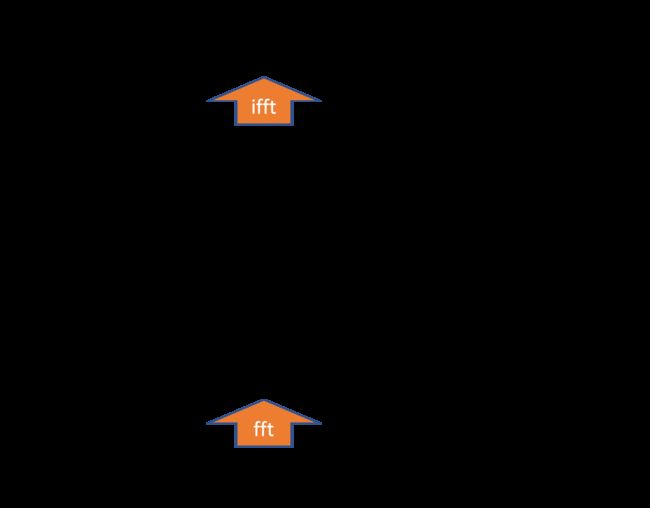
-
对于形如式 % \eqref{3-11} 的偏微分方程 (组), 通过变量代换将其中的 ∂ n u / ∂ t n \partial^n u / \partial t^n ∂nu/∂tn 降为 1 阶 导数, 若 n = 1 n=1 n=1, 略过此步.
-
在 x x x 域上对偏微分方程 (组) 做傅里叶变换, 则线性项中的 ∂ n u / ∂ x n \partial^n u / \partial x^n ∂nu/∂xn 直接变为 ( i k ) n u ^ (\mathrm{i} k)^n \hat{u} (ik)nu^, 并利用 u = F − 1 [ u ^ ] 、 ∂ n u / ∂ x n = F − 1 [ ( i k ) n u ^ ] u=F^{-1}[\hat{u}] 、 \partial^n u / \partial x^n=F^{-1}\left[(\mathrm{i} k)^n \hat{u}\right] u=F−1[u^]、∂nu/∂xn=F−1[(ik)nu^] 代换非线性项中的 u 、 ∂ n u / ∂ x n u 、 \partial^n u / \partial x^n u、∂nu/∂xn, 得到关于 u ^ ( k , t ) \hat{u}(k, t) u^(k,t) 的微分方程 (组).
-
用时间步进法 (如龙格-库塔法等) 数值计算离散化的关于 u ^ ( k , t ) \hat{u}(k, t) u^(k,t) 的微分方程组, 默认边界条件为周期性边界条件, 初始条件 u ^ ( k , t 0 ) = F [ u ( x , t 0 ) ] \hat{u}\left(k, t_0\right)=F\left[u\left(x, t_0\right)\right] u^(k,t0)=F[u(x,t0)] .
-
将上一步得到的结果从频域变换回空域, 即: u ( x , t ) = F − 1 [ u ^ ( k , t ) ] u(x, t)=F^{-1}[\hat{u}(k, t)] u(x,t)=F−1[u^(k,t)] .离散傅里叶变换及逆变换由
fft、ifft函数实现.
傅里叶谱方法求解基本偏微分方程—一维波动方程
对于一根两端固定、没有受到任何外力的弦, 若只研究其中的一段, 在不太长的时间里, 固定端来不及对这段弦产生影响, 则可以认为固定端是不存在的, 弦的长度为无限大。 这种无界 ( − ∞ < x < ∞ ) (-\infty
∂ 2 u ∂ t 2 = a 2 ∂ 2 u ∂ x 2 \frac{\partial^2 u}{\partial t^2}=a^2 \frac{\partial^2 u}{\partial x^2} % \label{111} ∂t2∂2u=a2∂x2∂2u
如果保证数值计算的区间足够大, 在一定时间内, 弦的振动范围始终没有超出计算区间 (或可以近似地这么认为), 那么就能够放心地使用周期性边界条件。取 a = 1 a=1 a=1, 初始条件为:
u ∣ t = 0 = 2 sech ( x ) , ∂ u ∂ t ∣ t = 0 = 0 \left.\quad u\right|_{t=0}=2 \operatorname{sech}(x),\left.\quad \frac{\partial u}{\partial t}\right|_{t=0}=0 u∣t=0=2sech(x),∂t∂u t=0=0
在数学物理方法中, 无界弦的自由振动可由行波法求出解析解, 即达朗贝尔公式。 根据达朗贝尔公式, 从 t = 0 t=0 t=0 开始, 长度为 L = 80 L=80 L=80 的 u u u 的初始状态 2 sech ( x ) 2 \operatorname{sech}(x) 2sech(x) 将分裂为两个 sech 形的波, 分别向两边以速度 a = 1 a=1 a=1 经过 T = 20 T=20 T=20 秒传播出去, 即正行波和反行波。下面用傅里叶谱方法求解无界弦的自由振动问题, 并与达朗贝尔公式的预测进行比较。首先引入函数 v v v 对式 % \eqref{111} 进行降阶:
{ ∂ u ∂ t = v ∂ v ∂ t = a 2 ∂ 2 u ∂ x 2 \left\{\begin{array}{l} \frac{\partial u}{\partial t}=v \\ \frac{\partial v}{\partial t}=a^2 \frac{\partial^2 u}{\partial x^2} \end{array}\right. {∂t∂u=v∂t∂v=a2∂x2∂2u
对上式等号两边做傅里叶变换(连续), 化为偏微分方程组:
{ ∂ u ^ ∂ t = v ^ ∂ v ^ ∂ t = − a 2 k 2 u ^ \left\{\begin{array}{l} \frac{\partial \hat{u}}{\partial t}=\hat{v} \\ \frac{\partial \hat{v}}{\partial t}=-a^2 k^2 \hat{u} \end{array}\right. {∂t∂u^=v^∂t∂v^=−a2k2u^
注意,以上操作均在连续系统下进行,未做离散近似。
接下来开始构建数值格式,首先,对区间 [ − L 2 , L 2 ] [-\frac{L}{2},\frac{L}{2}] [−2L,2L] 做空间剖分,得到空域信号序列 u 1 , . . . , u j , . . . , u N u_1,...,u_j,...,u_N u1,...,uj,...,uN 在 x x x 轴上的坐标间隔是 L / N L/N L/N , 相应的横坐标 x x x 可认为是:
− L / 2 , − L / 2 + L / N , … , L / 2 − 2 L / N , L / 2 − L / N -L/2,-L/2+L/N,\ldots,L/2-2L/N,L/2-L/N −L/2,−L/2+L/N,…,L/2−2L/N,L/2−L/N
此时可使用 Matlab 中 fft 函数做离散傅立叶变换,需要注意的是,fft 函数输出的序列 u ^ 1 , . . . , u ^ k , . . . , u ^ N \hat{u}_1,...,\hat{u}_k,...,\hat{u}_N u^1,...,u^k,...,u^N 所对应的频率并不是按照从小到大的顺序排列的,而是非负频率对应于前半部分序列,负频率对应于后半部分序列,即相应的横坐标 k k k 可认为是:
0 , 2 π / L , 4 π / L , … , ( N − 4 ) π / L , ( N − 2 ) π / L , − N π / L , − ( N − 2 ) π / L , … , − 4 π / L , − 2 π / L 0,2\pi/L,4\pi/L,\ldots,(N-4)\pi/L,(N-2)\pi/L,-N\pi/L,-(N-2)\pi/L,\ldots,-4\pi/L,-2\pi/L 0,2π/L,4π/L,…,(N−4)π/L,(N−2)π/L,−Nπ/L,−(N−2)π/L,…,−4π/L,−2π/L
因此 Matlab 提供了 fftshift 函数,用于调整 fft 输出序列的顺序。也就是说,fftshift(fft(u)) 所对应的频率才是按照递增顺序排列的:
− N π / L , − ( N − 2 ) π / L , … , − 2 π / L , 0 , 2 π / L , … , ( N − 4 ) π / L , ( N − 2 ) π / L -N\pi/L,-(N-2)\pi/L,\ldots,-2\pi/L,0,2\pi/L,\ldots,(N-4)\pi/L,(N-2)\pi/L −Nπ/L,−(N−2)π/L,…,−2π/L,0,2π/L,…,(N−4)π/L,(N−2)π/L
此外还有 ifftshift 函数用于进行与 fftshift 函数相反的操作。实际上,fftshift 函数的作用仅是让 fft 的输出结果变得更易于观察,若还需要用 ifft 函数将频谱信息还原回空域信号,就必须在使用 fftshift 之后再用 ifftshift 函数将序列的顺序恢复,否则得不到正确结果。如果不是为了分析频谱信息,而此处目的是通过傅里叶谱方法处理微分问题,则大可不必使用 fftshift 和 ifftshift 函数调整序列的顺序,而是在代码中通常使用顺序颠倒的频域坐标,以减少代码冗余、 节约时间。
以求序列 u 的二阶导数数值解为例:ifft((i*k).^2.*fft(u))。其中,变量 k 是由 Matlab 语句 (2*pi/L)*[0:N/2-1 -N/2:-1] 生成的顺序颠倒的频域坐标,这样做是为了免去调用 fftshift 和 ifftshift 的步骤。
这样就可以用 ode45 求解了, 详细代码如下:
主程序代码如下:
clear all; close all;
L=80;N=256;
x=L/N*[-N/2:N/2-1];
k=(2*pi/L)*[0:N/2-1 -N/2:-1].';
% 初始条件
u=2*sech(x);ut=fft(u);
vt=zeros(1,N);uvt=[ut vt];
% 求解
a=1;t=0:0.5:20;
[t,uvtsol]=ode45('wave1D',t,uvt,[],N,k,a);
usol=ifft(uvtsol(:,1:N),[],2);
% 画图
p=[1 11 21 41];
for n=1:4
subplot(5,2,n)
plot(x,usol(p(n),:),'k','LineWidth',1.5),xlabel x,ylabel u
title(['t=' num2str(t(p(n)))]),axis([-L/2 L/2 0 2])
end
subplot(5,2,5:10)
waterfall(x,t,usol),view(10,45)
xlabel x,ylabel t,zlabel u,axis([-L/2 L/2 0 t(end) 0 2])
文件 wave1D.m 代码如下:
function duvt=wave1D(t,uvt,dummy,N,k,a)
ut=uvt(1:N);vt=uvt(N+[1:N]);
duvt=[vt;-a^2*(k).^2.*ut];
end
计算结果如图所示, 初始状态的波形分裂成两半, 并分别向 x x x 轴正方向和负方向 以速度 a a a 运动, 这和达朗贝尔公式给出的结论是一致的。

傅里叶谱方法求解基本偏微分方程—二维波动方程
将一维波动方程中的一维无界弦自由振动方程推广到二维空间上, 就得到了描述无界 ( − ∞ < x , y < ∞ ) (-\infty
∂ 2 u ∂ t 2 = a 2 ( ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 ) u \frac{\partial^2 u}{\partial t^2}=a^2\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right) u % \label{222} ∂t2∂2u=a2(∂x2∂2+∂y2∂2)u
取 a = 1 a=1 a=1, 初始条件为:
u ∣ t = 0 = e − 20 [ ( x − 0.4 ) 2 + ( y + 0.4 ) 2 ] + e − 20 [ ( x + 0.4 ) 2 + ( y − 0.4 ) 2 ] , ∂ u ∂ t ∣ t = 0 = 0 \left.u\right|_{t=0}=\mathrm{e}^{-20\left[(x-0.4)^2+(y+0.4)^2\right]}+\mathrm{e}^{-20\left[(x+0.4)^2+(y-0.4)^2\right]},\left.\quad \frac{\partial u}{\partial t}\right|_{t=0}=0 u∣t=0=e−20[(x−0.4)2+(y+0.4)2]+e−20[(x+0.4)2+(y−0.4)2],∂t∂u t=0=0
可以这样理解上述初始条件的物理意义: 两手抓住弹性薄膜的两个位置, 分别提起, 使薄膜上形成两个峰, 在 t = 0 t=0 t=0 时刻突然松手。根据生活常识可以预料到, 这两个位置的薄 膜将来回振动, 与此同时, 产生的波向四周传播, 而且波与波会在相遇处叠加。
为便于求解, 引入函数 v v v 对式 % \eqref{222} 进行降阶, 得:
{ ∂ u ∂ t = v ∂ v ∂ t = a 2 ( ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 ) u \left\{\begin{array}{l} \frac{\partial u}{\partial t}=v \\ \frac{\partial v}{\partial t}=a^2\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right) u \end{array}\right. {∂t∂u=v∂t∂v=a2(∂x2∂2+∂y2∂2)u
对上式等号两边做傅里叶变换, 得到常微分方程组:
{ ∂ u ~ ^ ∂ t = v ^ ^ ∂ v ^ ^ ∂ t = − a 2 ( k x 2 + k y 2 ) u ^ ^ \left\{\begin{array}{l} \frac{\partial \hat{\tilde{u}}}{\partial t}=\hat{\hat{v}} \\ \frac{\partial \hat{\hat{v}}}{\partial t}=-a^2\left(k_x^2+k_y^2\right) \hat{\hat{u}} \end{array}\right. {∂t∂u~^=v^^∂t∂v^^=−a2(kx2+ky2)u^^
接下来用 ode45 求解即可, 代码如下:
主程序代码如下:
clear all; close all;
L=4;N=64;
x=L/N*[-N/2:N/2-1];y=x;
kx=(2*pi/L)*[0:N/2-1 -N/2:-1];ky=kx;
[X,Y]=meshgrid(x,y);
[kX,kY]=meshgrid(kx,ky);
K2=kX.^2+kY.^2;
% 初始条件
u=exp(-20*((X-0.4).^2+(Y+0.4).^2))+exp(-20*((X+0.4).^2+(Y-0.4).^2));
ut=fft2(u);vt=zeros(N);uvt=[ut(:); vt(:)];
% 求解
a=1;t=[0 0.25 0.5 1];
[t,uvtsol]=ode45('wave2D',t,uvt,[],N,K2(:),a);
% 画图
for n=1:4
subplot(2,2,n)
mesh(x,y,ifft2(reshape(uvtsol(n,1:N^2),N,N))),view(10,45)
title(['t=' num2str(t(n))]),axis([-L/2 L/2 -L/2 L/2 0 1])
xlabel x,ylabel y,xlabel x,zlabel u
end
文件 wave2D.m 代码如下:
function duvt=wave2D(t,uvt,dummy,N,K2,a)
ut=uvt(1:N^2);vt=uvt(N^2+[1:N^2]);
duvt=[vt;-a^2*K2.*ut];
end
程序输出结果如图所示, 它反映了弹性薄膜上的波向四周传播的过程。
