刷题笔记 leetcode 189.轮转数组（中等）

题目

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

提示：

• 1 <= nums.length <= 105

• -231 <= nums[i] <= 231 - 1

• 0 <= k <= 105

进阶：

尽可能想出更多的解决方案，至少有 三种 不同的方法可以解决这个问题。

你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？

来源：力扣（LeetCode）

链接：https://leetcode.cn/problems/rotate-array

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

方法一：辅助数组

先看提示，这是做题的好习惯。提示很容易让我们想到之前没想到的一些边界情况。

数组长度为1~10^5^ ,需要轮转的位数k也为1~10^5^ 。也就是说 有可能出现轮转位数比数组长度还要更长的情况。因此，我们需要首先对k取余。确保我们之后的轮转操作不会超出数组的空间。

首先我们能够想到最简单解题方法就是另外开辟出等长的数组，将旧数组后k位放至新数组的前k位，再将旧数组的前n-k位放至新数组的后n-k位，最后将新数组复制给旧数组即可实现题目要求。

AC代码

时空复杂度

时间复杂度：仅用了一次for循环，因此时间复杂度位O(N)

空间复杂度：由于另外开辟了一个与原数组等长数组空间，因此空间复杂度为O(N)

这也是典型的以空间换时间的解题思路。容易想到，但是内存消耗较大。

方法二：三次反转

在思路一中，我们提出了以空间换时间的方法，那么有没有一种方法能够在不开辟额外的空间便能实现题目所需效果呢？答案是可以的。

首先 我们通过观察可以得到，所谓的数组轮转，可以通过多次翻转数组来实现。下面以图的方式来直观表达。

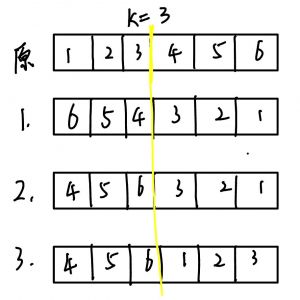
如上图 我们要对[1,2,3,4,5,6]的数组向右乱转k=3位。

将整个数组[0,n-1]整体反转为[6,5,4,3,2,1]

将[0,k-1]部分翻转 为[4,5,6,3,2,1]

将[k,n-1]部分反转为[4,5,6,1,2,3]

这样我们就实现了题目要求。

AC代码

时空复杂度

时间复杂度：调用了三次while循环 时间复杂度为O(N)

空间复杂度: 没有开辟新的数组空间 空间复杂度为O(1)

本题与Day3:剑指 Offer 58 - II. 左旋转字符串（简单）基本类似。只多了一个取余操作。