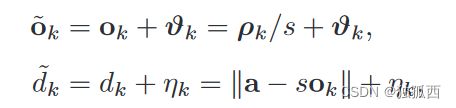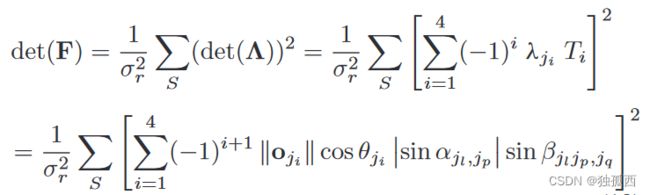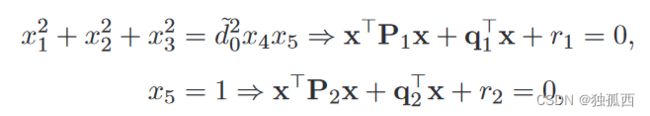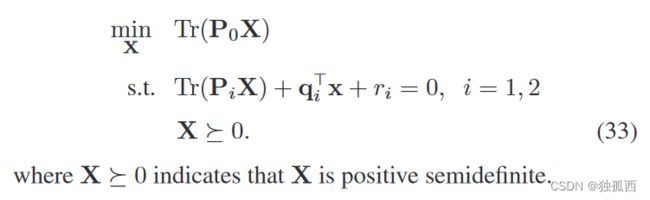论文阅读：Estimating Odometry Scale and UWB Anchor Location Based on Semidefinite ProgrammingOptimization

前言

2022年发表在RAL上的一篇论文，研究了里程计系统的未知度量尺度估计问题和超宽带( Ultra-wideband，UWB )锚点在环境中的三维定位问题。这篇文章的作者Thien Hoang Nguyen是UWB-VIO领域的主要研究人员，从最近一年的成果来看，他的研究方向从之前的注重UWB-VIO融合定位转变到现在的对UWB-VIO中更加精细问题的处理，以及UWB-VIO传感器融合在其他位姿估计场景下的应用。这篇文章就也是没有去卷UWB-VIO的定位精度，而注重于更好地解决UWB-VIO定位中的里程计尺度估计和UWB锚点估计这两个问题。

一、问题背景

单机器人或多机器人系统在未知环境中的导航挑战可能来自于GPS信号的缺乏，不良的视觉条件(低照度、感知混叠、几何特征稀缺等。)，不可靠的通信链路，有限的传感器视场等等。传统的基于UWB的定位方法需要在工作区域安装足够数量的锚节点，并对其位置进行预校准。如果锚节点只能在任务期间部署，例如搜索和救援场景，UWB网络可能只由一个位置未知的锚节点组成，这使得现有的方法不适用。对于机器人上只有单个相机可用的小型机器人，单目视觉里程计问题是尺度模糊。通过一个额外的IMU，在精确的时空内在和外在校准的情况下，可以精确地恢复度量尺度。尽管如此，在所有轴上没有完全激励运动的情况下，刻度仍然可能是不可观测的，错误的或会随时间漂移，这需要在线校准过程来校正。因此在这项工作中，我们专注于机器人只有在未知位置访问单目视觉里程计( VO )系统和单个测距锚点提供的高尺度里程计数据的情况。这样的系统将是一般的，从这个意义上说，分析也是适用的。

UWB辅助定位的过去的工作侧重于系统集成(将UWB技术与现有的传感器技术相结合)，而没有研究机器人的运动如何影响锚点位置的可观测性。据我们所知，现有文献中还没有关于尺度和锚点位置的可观测性分析。

最后，众所周知，基于测距的目标定位算法的精度强烈依赖于机器人轨迹，即应该使用或避免何种类型的轨迹来改善估计结果。

二、主要假设

单目相机与单个未知UWB锚点

三、理论流程

问题建模

VO和UWB的测量模型：

利用信息：

 目标估计量：

理论分析

1、Fisher信息矩阵

依据

[20] S. Ponda, R. Kolacinski, and E. Frazzoli, “Trajectory optimization for target localization using small unmanned aerial vehicles,” in Proc. AIAA Guid., Navigation, Control Conf., 2009, Art. no. 6015.

[21] Z. Wang and G. Dissanayake, “Observability analysis of SLAM using fisher information matrix,” in Proc. 10th Int. Conf. Control, Automat., Robot. Vis., 2008, pp. 1242–1247.

[22] H. C. So, Handbook of Position Location: Theory, Practice, and Advances, vol. 27. Hoboken, NJ, USA: Wiley, 2011.

这三篇文献进行理论介绍。

度量随机变量 X 所含有的关于其自身随机分布函数的未知参数 θ 的信息量。Fisher信息越大，Score function的方差越大，代表的信息越多，对参数估计的准确度越高。<所以可以用作一种衡量指标判别模型或算法>

由于det ( F )与不确定量成反比，所以det ( F )越小，估计的可达方差越大，或者说问题越困难。而且，可以看出：

一般而言，采集的测量值越多( S越大)，测量值越准确( σr越小)，det ( F )越大，不确定度越小。

若机器人为静止(‖oi‖= 0∂i)或动直线(所有的ui向量是共面的,因此Ti = 0∑i)，则det ( F )为0，系统不可观测。

如果尺度因子s很大，无论轨迹形状如何，‖o‖都会很小，那么det ( F )也会接近于零。直观上，这是因为从位置数据上看，机器人实际是在移动还是停留在一个地方是无法辨别的。

2、奇异构型分析

如果FIM是奇异的，则系统是不可观测的[ 21 ]。因此，我们感兴趣的是找到导致奇异性的轨迹形状，以便在实际中避免它们。我们有rank ( F ) = rank ( J ) .因此，FIM非奇异当且仅当雅克比J∈Rk × 4为满列秩，其中k为测量次数，4为状态向量维数。

可以通过J的结构来研究系统和每个状态的可观测性。当k < 4时，FIM显然不能满秩。当k≥4时，J是奇异的当且仅当它的列向量线性相关，即存在超定齐次线性系统( OHLS )的非平凡解C∈R4 .

注意到上面这一结果也适用于尺度因子已知的情况，因为J的最后一列被有效地移除。因此，UWB锚点位置可观测的充要条件是所有相对位置向量ri的集合不是R3的子空间

总的来说，FIM是奇异的，如果：( 1 )所有的相对位置矢量ri是共面的，( 2 )机器人在由描述的球面上移动，其中c是R3中的任何向量，或者( 3 ) ( 1 )和( 2 )的组合。图2给出了一个例子。

提出方法

理论支撑：

[24] P. Biswas, T.-C. Liang, K.-C. Toh, Y. Ye, and T.-C. Wang, “Semidefinite programming approaches for sensor network localization with noisy distance measurements,” IEEE Trans. Automat. Sci. Eng., vol. 3, no. 4, pp. 360–371, Oct. 2006.

[25] A. M.-C. So and Y. Ye, “Theory of semidefinite programming for sensor network localization,” Math. Program., vol. 109, no. 2/3, pp. 367–384, Sep. 2006.

[26] N. Trawny and S. I. Roumeliotis, “On the global optimum of planar, rangebased robot-to-robot relative pose estimation,” in Proc. IEEE Int. Conf. Robot. Automat., 2010, pp. 3200–3206. [27] Z.-Q. Luo, W.-K. Ma, A. M.-C. So, Y. Ye, and S. Zhang, “Semidefinite relaxation of quadratic optimization problems,” IEEE Signal Process. Mag., vol. 27, no. 3, pp. 20–34, May 2010.

[28] J. Nocedal and S. J. Wright, Numerical Optimization. Berlin, Germany: Springer, 1999.

1、SDP松弛

原始问题：

经过推到整理，可以重新表述为二次形式：

转化为如下的非凸QCQP问题：

其中约束条件由x的参数之间的关系得出如下：

获得QCQP问题的SDP松弛和恢复原解的步骤在文献[ 27 ]中已经很好地建立，为简洁起见省略。综上，令X = xxT为新变量，我们要解决的SDP松弛问题为：

2、轨迹优化

最优轨迹：通过研究最大化det ( F )的条件，可以得到最优轨迹。虽然对于一般情况下的最优轨迹如何看起来并不简单，但可以对子问题进行如下分析：

仅估计a：状态向量退化为Θ：= a。按照同样的推导步骤，我们有：

因此，文献[ 16 ]的分析仍然适用：给定固定的测量次数k，增大感知位置之间的张角一般会减小定位误差；由于实际的传感位置不相关，最优轨迹并不唯一；绕UWB锚点的圆周运动轨迹是一个最优解。

仅估计s：将状态向量约化为仅有Θ：= s且我们有：

机器人在一条经过世界坐标系原点和UWB锚点位置(图1中的Wa线( a )) )的直线上运动，且‖oi‖尽可能大，即机器人在UWB感知范围内尽可能远离原点运动

综合分析，一般情况下的最优轨迹应该是一个折中的解决方案：感知位置应该围绕UWB锚点，其中一些位置位于Wa线上，但机器人不会直接在Wa线上移动。

在线轨迹：对于在线操作，由于种种原因，如上所述的最优轨迹可能不实用。首先，UWB锚点位置的初始猜测可能是不准确的或不可用的，这意味着在每个执行步骤后都要更新轨迹。其次，随着k的增加，算法的复杂度和计算量都有可能无限增长。第三，由于环境中的未知障碍物或平台的运动约束，优化后的轨迹可能无法执行。因此，我们提出了如下的分步轨迹优化方法。

我们对机器人轨迹采用离散时间常速度模型，该模型由下式给出

在每个时间步，在采取新的测量后，SDP估计量更新( Θ )的估计值。轨迹优化问题，其目的是找到最佳的取点位置下一步的测量，公式为

最小化不确定性椭球体积的D -最优目标函数式( 37 )是目标跟踪问题的流行选择[ 20 ]。

约束式( 38 )限制了机器人的最大速度，而约束式( 39 )对应UWB传感器的最大测距距离。该优化问题可以用数值序列二次规划( SQP )方法求解[ 28 ]。

我们的轨迹优化问题比较简单，因为我们专注于评估轨迹形状，但可以添加其他成本，如能量、时间或跟踪误差，以制定一个通用的路径规划问题。同样，约束的数量可以很容易地扩展，例如最大加速度(‖vk + 1 - vk‖/ T≤amax)，最大运动半径(‖( ρk + 1‖≤Rmax)，避碰(‖[ ( ρk + 1-obsi‖≥ri⋅i)等。然而，我们的流水线的一个潜在缺点是性能取决于估计器如何首先初始化[ 20 ]，这反过来又取决于机器人的第一轮运动。

四、实验方案

里程计尺度和锚点估计

仿真设计如下。对于给定的世界原点和锚点位置之间的距离( d0 )，进行了N = 100的模拟。在每次仿真中，尺度因子s在( 0，10 ]之间随机采样，锚点位置a在圆心为原点、半径为d0的球体上均匀采样，真实的机器人轨迹由M = 20个位置组成，从原点出发，在给定的半径R内随机运动，即ρ 1 = 0，‖ρi‖≤R∂i∈[ 2 , ... , M]。然后由地面真值生成里程计和测距数据并添加噪声，其中所有不同坐标轴的里程计噪声设置与σ x，y，z = σ o类似。

性能指标包括UWB锚点位置( et )和尺度因子( es )估计误

轨道最优化

评价过程如下。首先，进行螺旋运动以提供M = 20个初始数据点。然后，进行SDP估计器-轨迹优化-执行的过程。设采样周期为T = 1s，最大速度为vmax = 1m / s，最大测距距离为dmax = 50m。所提出的方法与随机运动( RM )策略(随机选取vk∈R3 ,使得‖vk‖= vmax)进行了比较。我们让这些方法运行k = 200步，并记录结果。

自由运动和约束运动。

总体而言，我们的轨迹优化方法速度足够快，可以达到实时性能，但对于实际应用，可能需要调整采样周期。

五、创新总结

本文研究了利用升尺度里程计和UWB测距数据的里程计尺度和锚点位置估计问题。与我们最近的工作[ 19 ]相比，本文分享了如何推导FIM和设计SDP估计量的一般思路。然而，由于包含了比例因子，这些公式是新的，而不是直接从[ 19 ]中推导出来的。此外，我们还提供了文献[ 19 ]中没有的奇异位形分析、最优轨线分析和在线优化方法。

推导尺度和单个UWB锚点位置估计问题的FIM及其行列式；

基于FIM的奇异案例分析，对奇异案例进行几何解释；一个估计-轨迹优化框架包括：

1 )我们在[ 19 ]中介绍的基于SDP的估计方法的变体适应于本工作中的问题；

2 )提出了一种基于FIM的轨迹优化方法，增强了估计结果，并且易于扩展到不同的实际应用中。

在本文中，研究了利用尺度上的里程计和机器人到锚点的测距数据进行尺度和3D UWB锚点位置估计的问题。

给出了问题的FIM的推导，揭示了机器人的轨迹如何影响每个参数的信息增益以及在实际中应该规避的奇异情况。

提出了一种由SDP方法组成的估计-轨迹优化管道，该方法利用参数之间的关系来寻找解决方案，并基于FIM提出了一种简单但可扩展的轨迹优化方法。

仿真结果表明，估计器比以前的方法更准确和鲁棒，而轨迹优化比以前采用的随机运动具有更快的收敛速度。

在真实系统中进行实验，并扩展到一般的多机器人，采用去中心化技术的多锚案例是未来工作的主要目标。