【隐私计算】VOLE (Vector Oblivious Linear Evaluation)学习笔记

近年来，VOLE（向量不经意线性评估）被用于构造各种高效安全多方计算协议，具有较低的通信复杂度。最近的CipherGPT则是基于VOLE对线性层进行计算。

1 VOLE总体设计

VOLE的功能如下，VOLE发送$\Delta$和$b$给sender，发送$a$和$c$给receiver，并且$c,a,b$满足线性关系：$c=\Delta \cdot a+b$。

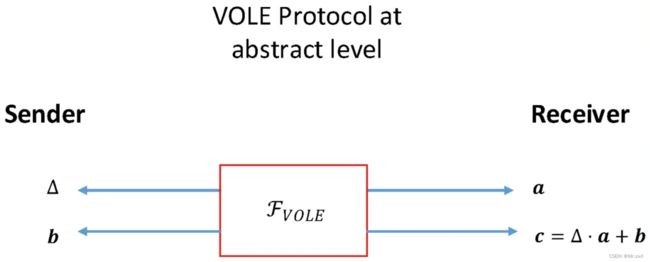
现在主流的VOLE是基于LPN (Learning with Parity Noise)假设/问题来构造的。

2 基于LPN假设的VOLE构造

2.1 前置知识

1 LPN假设
LPN是一个重要的抗量子计算的困难问题。事实上，解决LPN问题等价于解决编码理论中的随机线性码纠错问题（Decoding a random linear code problem）。LPN的表述为：

1. 随机生成矩阵$A$
2. 随机生成秘密（行）向量$s$
3. 随机生成错误（行）向量$e$，满足$HW(e)=r\cdot n$，其中，参数$r$是噪声比率
4. 计算向量$b=s\cdot A+e$

则有$(A,b){\approx }_c(A^{\prime },b^{\prime })$，其中，$(A^{\prime },b^{\prime })$是随机生成的。解决LPN问题即使是解决如下问题：给定$A,b$，求解$s,e$的值。
在密码实践中，为了保证具体的LPN参数设定是困难的，通常选取较大的$k$，较大的$n$以及较小的$r$。

2 函数秘密分享（Functional Secret Sharing, FSS）
FSS它允许计算$P_0,P_1$合作计算某个函数$f$在某个点上的估值$f(x)$。计算完成后，$P_0$得到一份share为$f_0(x)$，$P_1$得到另一份share为$f_1(x)$，满足$f(x)f=f_0(x)+f_1(x)$，其中，$f_0(x),f_1(x)$是伪随机的。
FSS形式化定义如下：
给定函数$f$，FSS定义了一对算法$(Gen,Eval)$：

• $FSS.Gen(1^{\lambda },f)$：给定安全参数$\lambda$和函数$f$，生成一对密钥$(K_0,K_1)$
• $FSS.Eval(b,K_b,x)$：给定参与方索引$b\in \{0,1\}$，密钥$K_b$和函数输入$x$，输出$f_b\in \mathbb{G}$（$\mathbb{G}$表示群）

由此可见，在FSS过程中，涉及到AES对称加密。

3 VOLE生成器
VOLE定义了两个算法，即$VOLE=(Setup,Expand)$：

• $Setup(1^{\lambda },\mathbb{F},n,x)$：输出一对种子$(see{d}_0,see{d}_1)$，其中，$see{d}_1$包含输入$x$
• $Expand(\sigma ,see{d}_{\sigma })$：如$\sigma =0$，输出$(u,v)$；如$\sigma =1$，输出$w$

于是VOLE满足以下正确性：
$(u,v)\leftarrow Expand(0,see{d}_0),w\leftarrow Expand(1,see{d}_1)$，满足$w=u\cdot x+v$。

2.2 VOLE的构造方法

现在介绍如何定义Setup和Expand算法，直觉就是在Setup中分配给$P_0,P_1$的种子$see{d}_0,see{d}_1$就具有某种线性关系，同时在Expand时仍保持这种线性关系。

尝试1
Setup构造如下：
$see{d}_0\leftarrow (a,b){\in }_R{\mathbb{F}}^k\times {\mathbb{F}}^k,see{d}_1\leftarrow (c=a\cdot x+b,x)\in {\mathbb{F}}^k\times \mathbb{F}$
其中$(a,b)$是随机生成的，因此$c$也是随机的。
Expand构造如下：
随机生成一个矩阵$C\in {\mathbb{F}}^{k\times n}(k<n)$，并将$C$作为公开参数发布出去，然后计算：
$Expand(0,see{d}_0)=(a\cdot C,b\cdot C),Expand(1,see{d}_1)=c\cdot C$
由此可见，Expand保持了$a,b,c$的线性关系，并把种子的长度从$k$扩展到了$n$。

尝试2
但是上面的构造方式并非伪随机【这里我不是很理解】，借助LPN假设来解决这个问题，Expand构造如下：
$Expand(0,see{d}_0)=(a\cdot C+\mu ,b\cdot C-{\nu }_b),Expand(1,see{d}_1)=c\cdot C+{\nu }_c$
根据LPN可知Expand算法的输出是伪随机的【具体原因？】，但是线性关系难以满足，因为这里${\nu }_c\ne \mu \cdot x-{\nu }_b$，但是如果可以限制${\nu }_c=\mu \cdot x-{\nu }_b$也就是${\nu }_b+{\nu }_c=\mu \cdot x$，线性关系就维持住了。幸运的事，依靠FSS可以生成伪随机${\nu }_b,{\nu }_c$满足这个关系。

正式构造
假设LPN假设中公开参数为$\mathbb{F},k,n,t=rn,C\in {\mathbb{F}}^{k\times n}$，则VOLE生成器$G$可以定义为：
$Setup(1^{\lambda },x)$：

1. 随机生成$(a,b)\in {\mathbb{F}}^k\times {\mathbb{F}}^k$，随机生成$\mu \in {\mathbb{F}}^n$，满足$HW(\mu )=t$
2. 计算$c=a\cdot x+b$
3. $(K_0,K_1)\leftarrow FSS.Gen(1^{\lambda },f)$，满足$FSS.Eval(0,K_0)+FSS.Eval(1,K_1)=x\cdot \mu$
4. $see{d}_0\leftarrow (K_0,\mu ,a,b),see{d}_1\leftarrow (K_1,x,c)$
5. 输出$see{d}_0,see{d}_1$

$Expand(\sigma ,see{d}_{\sigma })$：

1. 若$\sigma =0$，$see{d}_0=(K_0,\mu ,a,b)$，计算${\nu }_0\leftarrow FSS.Eval(0,K_0)$，输出$(u,v)\leftarrow (a\cdot C+\mu ,b\cdot C-{\nu }_0)$。即，尝试2中的$Expand(0,see{d}_0)=(a\cdot C+\mu ,b\cdot C-{\nu }_0)$
2. 若$\sigma =1$，$see{d}_1=(K_1,x,c)$，计算${\nu }_1\leftarrow FSS.Eval(1,K_1)$，输出$w\leftarrow c\cdot C+{\nu }_1$。即，尝试2中的$Expand(1,see{d}_1)=c\cdot C+{\nu }_1$

值得注意的是，${\nu }_0,{\nu }_1$的生成基于FSS，在Setup中满足$FSS.Eval(0,K_0)+FSS.Eval(1,K_1)=x\cdot \mu$，因此很容易得到：${\nu }_0+{\nu }_1=x\cdot \mu$，故现在的构造方法符合LPN伪随机性，并且满足线性关系。

3 VOLE在MPC乘法中的应用

在MPC中，安全加法很容易进行，只需在本地做加法即可。而乘法则是困难的，需要双方进行通信实现。
现在考虑乘法$z=xy$，其中，$x$在$P_0$方，$y$在$P_1$方，双方需要联合计算乘法结果。在算术秘密分享机制下，双方将自己的输入进行拆分，因此计算如下：
$$xy=(⟨x{⟩}_0+⟨x{⟩}_1)(⟨y{⟩}_0+⟨y{⟩}_1)=⟨x{⟩}_0⟨y{⟩}_0+⟨x{⟩}_1⟨y{⟩}_1+⟨x{⟩}_0⟨y{⟩}_1+⟨x{⟩}_1⟨y{⟩}_0$$
其中，前两项均可以在本地计算，而后两项（交叉项，CrossTerm）是MPC计算的重难点。
以$⟨x{⟩}_0⟨y{⟩}_1$为例，借助VOLE，让$P_0$计算出$v$【即上面Expand中的$v=b\cdot C-{\nu }_0$】， 让$P_1$计算出$w$【即上面Expand中的$w=c\cdot C+{\nu }_1$】，满足$⟨x{⟩}_0⟨y{⟩}_1=w-v$【$w-v={\nu }_0+{\nu }_1+c\cdot C-b\cdot C=u\cdot x+c\cdot C-b\cdot C$，其中$C$公开，$b\cdot C,c\cdot C$分别在两方计算出来，是明文了，因此$w-v$的结果也可算】，即可解决交叉项的计算问题。

4 基于VOLE生成器构造VOLE

VOLE生成器本质是一种伪随机数生成器，生成的两串伪随机数恰好是线性相关的。
预计算生成随机种子

1. 可信第三方（TTP）随机生成$r_x\in \mathbb{F}$
2. 调用VOLE生成器$G$，计算$(see{d}_0,see{d}_1)\leftarrow Setup(1^{\lambda },r)$
3. 将$see{d}_0$发给$P_0$，将$(r_x,see{d}_1)$发给$P_1$

预计算生成$(r_u,r_v,r_w)$

1. $P_0$计算$(r_u,r_v)\leftarrow Expand(0,see{d}_0)$
2. $P_1$计算$r_w\leftarrow Expand(1,see{d}_1)$

在线计算
现在$P_0$拥有$(u,v)$，$P_1$拥有$x$【于是，我们又回到了最开头那幅图】

1. $P_1$计算$m_x\leftarrow x-r_x$，并将$m_x$发给$P_0$
2. $P_0$计算$m_u\leftarrow u-r_u,m_v\leftarrow m_x{r}_u+v-r_v$，并发给$P_1$
3. $P_1$计算$w\leftarrow m_{u}x+m_v+r_w$

正确性
预计算阶段得到的随机向量满足$r_w=r_u\cdot r_x+r_v$，于是$P_1$方：
$$\begin{gathered} w=m_{u}x+m_v+r_w \\ =(u-r_u)x+(m_x{r}_u+v-r_v)+(r_u\cdot r_x+r_v) \\ =(u-r_u)x+((x-r_x)r_u+v-r_v)+(r_u\cdot r_x+r_v) \\ =ux-r_{u}x+r_{u}x-r_u{r}_x+v-r_v+r_u{r}_x+r_v \\ =ux+v \end{gathered}$$

这个形式和图中的$c=\Delta \cdot a+b$完全一致。由此可见，至此我们已经成功构造出VOLE的线性表达式。

参考资料

基于LPN假设构造VOLE