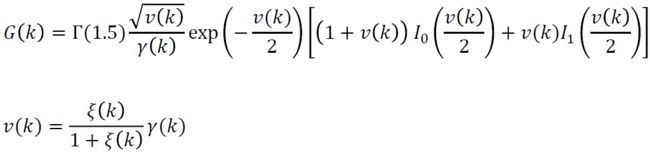语音信号处理——噪声抑制

简介

• 噪声抑制技术用于消除背景噪声，改善语音信号的信噪比和可懂度，让人和机器听的更清楚
• 常见的噪声种类：人声噪声、街道噪声、汽车噪声
• 噪声抑制方法的分类：
  • 按照输入通道数分：单通道降噪、多通道降噪
  • 按照噪声统计特性分：平稳噪声抑制、非平稳噪声抑制
  • 按照降噪方法分：被动降噪、主动降噪
• 下面介绍的方法用于单通道的、被动的、平稳噪声抑制

Minima Controlled Recursive Averaging（MCRA）

• 传统信号处理方法中降噪方法可分为两个大的步骤：

  • 一是对噪声的估计（Noise Estimation/Tracking）
  • 二是对增益因子的估计

• 噪声估计的常用方法：

  • 递归平均（Recursive Averaging）：只要某个频带中语音存在的概率很低，则可以利用这个频带估计/更新噪声谱
  • 最小值追踪（Minima Controlled/Tracking）：由于语音信号的稀疏性，即使语音存在，在一个短时窗内（0.5s-1.5s），每个频带的最小值也会大概率趋近于噪声功率，因此可以通过在短时窗内追踪最小值的方法获得每个频带的噪声估计
  • 直方图统计（Histogram-based Method）：带噪语音信号的每个频带在一个短时窗内做直方图统计，出现频次最高的值对应这个频带的噪声水平

• MCRA的步骤：

• 考虑带有加性噪声的数据模型：$y(n)=x(n)+d(n)$

• 输入信号经过STFT：$Y(k,l)={\sum }_{n=0}^{N-1}y(n+lM)h(n)e^{-j\frac{2\pi }{N}nk}$，得到时频谱图

• 其中，

  • k是frequency bin的索引
  • l是时间帧的索引
  • h(n)是窗函数
  • M是frame shift

• 给定两个假设$H_0(k,l)$和$H_1(k,l)$，分别表示“语音不存在”和“语音存在”：
  $$\begin{array}{rl}{H}_0(k,l)：& Y(k,l)=D(k,l)\\ H_1(k,l)：& Y(k,l)=X(k,l)+D(k,l)\end{array}$$

• 对噪声的估计定义为：${\lambda }_d(k,l)=E[|D(k,l){|}^2]$，也就是噪声的能量

• 采用时间递归平滑的方式，当“语音不存在”时，迭代更新${\lambda }_d(k,l)$
  $$\begin{array}{rl}{H}_0^{\prime }(k,l)：& {\hat{\lambda }}_d(k,l+1)={\alpha }_d{\hat{\lambda }}_d(k,l)+(1-{\alpha }_d)|Y(k,l){|}^2\\ H_1^{\prime }(k,l)：& {\hat{\lambda }}_d(k,l+1)={\hat{\lambda }}_d(k,l)\\ 其中，& {\alpha }_d（0<{\alpha }_d<1）是平滑因子\end{array}$$

• 语音存在概率（Speech Presence Probability）：$p^{\prime }(k,l)=P(H_1^{\prime }(k,l)|Y(k,l))$

• 对噪声的估计可表示为：
  $$\begin{array}{rl}{\hat{\lambda }}_d(k,l+1)& ={\hat{\lambda }}_d(k,l)p^{\prime }(k,l)+[{\alpha }_d{\hat{\lambda }}_d(k,l)+(1-{\alpha }_d)|Y(k,l){|}^2](1-p^{\prime }(k,l))\\ & ={\hat{\alpha }}_d(k,l){\hat{\lambda }}_d(k,l)+[1-{\hat{\alpha }}_d(k,l)]|Y(k,l){|}^2\\ 其中，{\hat{\alpha }}_d(k,l)& ={\alpha }_d+(1-{\alpha }_d)p^{\prime }(k,l)\end{array}$$

• 现在的问题是：如何确定$p^{\prime }(k,l)$

• 计算$p^{\prime }(k,l)$的思路：在一个短时窗内，计算局部能量$S(k,l)$与最小能量$S_{min}(k,l)$的比值

• 局部能量的计算：

  • 频域平滑：$S_f(k,l)={\sum }_{i=-w}^{w}b(i)|Y(k-i,l){|}^2$
  • 时域平滑：$S(k,l)={\alpha }_{s}S(k,l-1)+(1-{\alpha }_s)S_f(k,l)$
  • $b(i)$是频域窗函数，${\alpha }_s（0<{\alpha }_s<1）$是局部能量的时域平滑因子

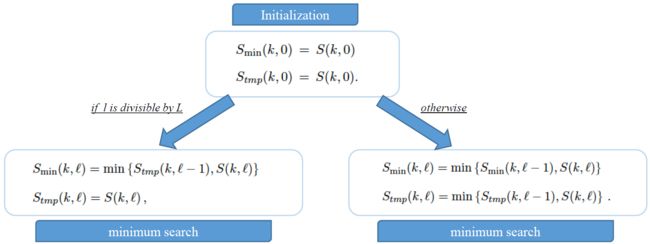
• 最小能量的计算：

  • 常规做法：采用局部最小值搜索的方法，设定一个时间窗L（L通常为1s），搜索局部最小值
  • 简化做法：
    

• 计算比值：$S_r(k,l)=\frac{S(k,l)}{S_{min}(k,l)}$

• 语音是否存在的判别式为：
  $$I(k,l)=\{\begin{array}{c}1，S_r(k,l)>\delta \\ 0，otherwise\end{array}$$

• 语音存在概率的迭代估计：

  • ${\hat{p}}^{\prime }(k,l)={\alpha }_p{\hat{p}}^{\prime }(k,l-1)+(1-{\alpha }_p)I(k,l)$
  • ${\alpha }_p（0<{\alpha }_p<1）$是语音存在概率的平滑因子

• MCRA噪声估计流程：
  

• MCRA参考参数
  

• 估计出噪声后，将带噪语音与增益因子相乘，即可进行噪声抑制
  $$\begin{array}{rl}\hat{X}(k,l)& =G(k,l)Y(k,l)\\ 或|\hat{X}(k){|}^2& =G^2(k)|Y(k){|}^2\end{array}$$

• 确定增益因子的方法：

  • 谱减法
  • 维纳滤波
  • MMSE

• 谱减法：假设噪声平稳或缓慢变化，从带噪语音谱中，将噪声谱减去

  • 增益因子的表达式：
    $$\begin{array}{rl}G(k)& =\sqrt{\frac{|\hat{X}(k){|}^2}{|Y(k){|}^2}}\\ & =\sqrt{\frac{|Y(k){|}^2-|\hat{D}(k){|}^2}{|Y(k){|}^2}}=\sqrt{\frac{|Y(k){|}^2-{\lambda }_d(k)}{|Y(k){|}^2}}\\ & =\sqrt{1-\frac{{\lambda }_d(k)}{|Y(k){|}^2}}=\sqrt{1-\frac{1}{\gamma (k)}}\end{array}$$
  • 其中，$\gamma (k)=\frac{|Y(k){|}^2}{{\lambda }_d(k)}$，被称为后验信噪比

• 频域维纳滤波：估计出的纯净语音幅度谱与真实幅度谱的均方误差最小

  • 频域估计误差：$E(k)=X(k)-\hat{X}(k)=X(k)-G(k)Y(k)$
  • 目标函数：$J=E[|E(k){|}^2]$
  • 最小化目标函数，可以得到增益因子的表达式：
    $$G(k)=\frac{{\lambda }_x(k)}{{\lambda }_x(k)+{\lambda }_d(k)}=\frac{\xi (k)}{\xi (k)+1}$$
  • 其中，${\lambda }_x(k)=E[|X(k){|}^2]$，$\xi (k)=\frac{{\lambda }_x(k)}{{\lambda }_d(k)}$被称为先验信噪比
  • 后验信噪比：$\gamma (k)=\frac{|Y(k){|}^2}{{\lambda }_d(k)}$
  • 先验信噪比：$\xi (k)=\frac{{\lambda }_x(k)}{{\lambda }_d(k)}$
  • 根据后验信噪比估计先验信噪比——判决引导法（Decision Directed，DD）
    $$\xi (k,l)={\alpha }_{DD}\frac{|\hat{X}(k,l-1){|}^2}{{\lambda }_d(k,l-1)}+(1-{\alpha }_{DD})max\{\gamma (k,l)-1,0\}$$
  • 其中，${\alpha }_{DD}$经验值为0.95~0.98，${\lambda }_d(k,l-1)$可用${\lambda }_d(k,l)$代替

• MMSE的增益因子：
  

• MMSE的推导可参考：Ephraim, Y., and D. Malah. “Speech Enhancement Using a Minimum-Mean Square Error Short-Time Spectral Amplitude Estimator.”