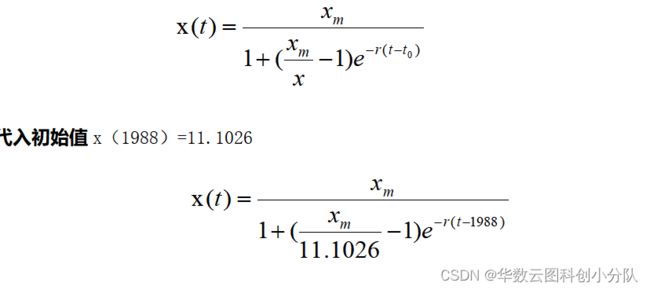数学建模-人口模型Logistic模型与 Malthus模型

一．问题及重述：下表是中国人口数据，请根据这些数据建立适当的数学模型对其进行描述，并预测2002、2003、2004年的中国人口数。

给出模型，求解代码及必要的图形，误差分析结果。

重述:

1. 选取合适的模型预测2002,2003、2004年的中国人口数；

建立数学模型、给出求解代码及必要的图形，误差分析结果

---

二．问题的分析和假设： 2-1对于问题一的分析 根据题目中的数据只是一个粗略预报人口总数的模型，没有对人口的年龄、性别、地域结构进行预报，故采用Malthus模型或Logistic模型 2-2对问题二的分析 我们通过使用数学知识和matlab对以上数据进行计算，进而求解，从而得到模型以及图像。 2-3对Logistic模型的假设 (1)设r(x)为x(t)的线性单调减函数，即r(x)＝r-sx(s>0)； (2)自然资源与环境条件所能容纳的最大人口数为Xm，即当x=时，增长率r()=0。 由（1）、（2）可得：

建模： 使用Logistic模型  上式是一个可分离变量性的微分方程，其解为： 以下对其进行拟合、求解以及绘图

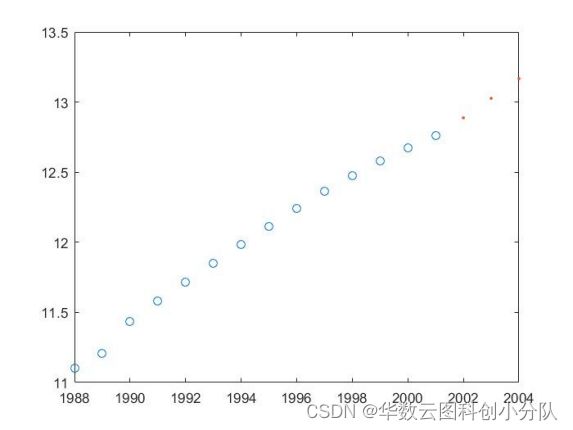
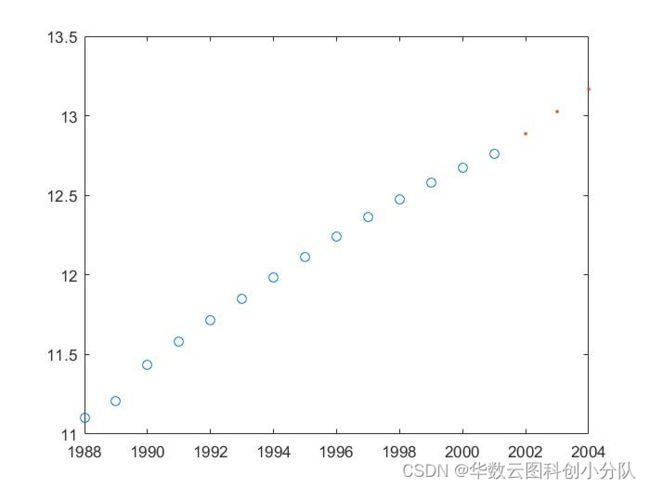
求解的Matlab程序代码：   编写M文件如下： Malthus模型:  首先对数据进行拟合： >> year=1988:1:2001; >>population=[11.1026,11.2074,11.4333,11.5823,11.7171,11.8517,11.9850 12.1121,12.2389,12.3626,12.4761,12.5786,12.6743,12.7627]; >> cftool                               图一  拟合数据图 Matlab自动生成的拟合代码： function [fitresult, gof] = createFit2(year, population) %CREATEFIT2(YEAR,POPULATION) %  Create a fit. % %  Data for 'untitled fit 1' fit: %      X Input : year %      Y Output: population %  Output: %      fitresult : a fit object representing the fit. %      gof : structure with goodness-of fit info. % %  另请参阅 FIT, CFIT, SFIT. %  由 MATLAB 于 06-Apr-2022 01:20:13 自动生成 %% Fit: 'untitled fit 1'. [xData, yData] = prepareCurveData( year, population ); % Set up fittype and options. ft = fittype( 'xm/(1+(xm/11.1026-1)*exp(-r*(t-1988)))', 'independent', 't', 'dependent', 'y' ); opts = fitoptions( 'Method', 'NonlinearLeastSquares' ); opts.Display = 'Off'; opts.StartPoint = [0.2 500]; % Fit model to data. [fitresult, gof] = fit( xData, yData, ft, opts ); % Plot fit with data. figure( 'Name', 'untitled fit 1' ); h = plot( fitresult, xData, yData ); legend( h, 'population vs. year', 'untitled fit 1', 'Location', 'NorthEast' ); % Label axes xlabel year ylabel population grid on 将以上代码保存当前文件夹，并在新的文件夹中调用这个函数得到参数的拟合值和预测的效果。 计算结果与结论：   通过Matlab进行计算，得到如下答案： >> year=1988:1:2001; >>population=[11.1026,11.2074,11.4333,11.5823,11.7171,11.8517,11.9850 12.1121,12.2389,12.3626,12.4761,12.5786,12.6743,12.7627]; cftool >>[fitresult, gof] = createFit1(year, population) >>t = 2002:2004; >>xm = 14.42;    >>r =  0.06451; >>predictions = xm./(1+(xm./11.1026-1).*exp(-r.*(t-1988))); >>figure(2) >>plot(year,population,'o',t,predictions,'.')   >>disp(predictions)   fitresult =      General model:      fitresult(t) = xm/(1+(xm/11.1026-1)*exp(-r*(t-1988)))      Coefficients (with 95% confidence bounds):        r =     0.06451  (0.05625, 0.07277)        xm =       14.42  (14.03, 14.82)

gof =            sse: 0.0038        rsquare: 0.9990            dfe: 12     adjrsquare: 0.9989           rmse: 0.0179    12.8624   12.9498   13.0328 图二  人口模型预测图 结论：当t=2002 时人口为12.8624亿、t=2003时人口为12.9498亿、t=2004时人口为13.0328亿。 误差分析：查询中国人口统计图表得出2002年为12.8亿 、2003年为12.88亿、2004年为12.96亿，发现两者几乎完全一致，Logistic模型的缺点是模型中的参数r和人口总数上限xm很难准确得到，尤其是xm的值还会随着人口发展变化的情况而改变。 建模： Malthus模型: 根据假设人口的净增长率是一个常数，也就是单位时间内人口增长量与当时人口数成正比,建立Malthus模型。 设t时刻人口数为x(t) ，t=t0时， x(t0) =x0，则： x(t + Dt) - x(t) = x(t) ×r × Dt 求解的Matlab程序代码：   Malthus模型:  首先对数据进行拟合： >> year=1988:1:2001; >>population=[11.1026,11.2074,11.4333,11.5823,11.7171,11.8517,11.9850 12.1121,12.2389,12.3626,12.4761,12.5786,12.6743,12.7627]; >> cftool                               图一  拟合数据图 Matlab自动生成的拟合代码： function [fitresult, gof] = createFit(year, population) %CREATEFIT(YEAR,POPULATION) %  Create a fit. % %  Data for 'untitled fit 1' fit: %      X Input : year %      Y Output: population %  Output: %      fitresult : a fit object representing the fit. %      gof : structure with goodness-of fit info. % %  另请参阅 FIT, CFIT, SFIT. %  由 MATLAB 于 05-Apr-2022 23:30:31 自动生成 %% Fit: 'untitled fit 1'. [xData, yData] = prepareCurveData( year, population ); % Set up fittype and options. ft = fittype( 'exp1' ); opts = fitoptions( 'Method', 'NonlinearLeastSquares' ); opts.Display = 'Off'; opts.StartPoint = [11.1026 0.0108]; % Fit model to data. [fitresult, gof] = fit( xData, yData, ft, opts ); % Plot fit with data. figure( 'Name', 'untitled fit 1' ); h = plot( fitresult, xData, yData ); legend( h, 'population vs. year', 'untitled fit 1', 'Location', 'NorthEast' ); % Label axes xlabel year ylabel population grid on 将以上代码保存当前文件夹，并在新的文件夹中调用这个函数得到参数的拟合值和预测的效果。 计算结果与结论：   通过Matlab进行计算，得到如下答案：  t=2002:2004; >> a = 6.16e-09 ; >>  b = 0.01072 ; >> predictions=a*exp(b*t); >> figure(2) >> plot(year,population,'o',t, predictions,'.') 图二  人口模型预测图 结论：当t=2002 时人口为12.89亿、t=2003时口为13.03亿、t=2004时人口为13.17亿。 误差分析：查询中国人口统计图表得出2002年为12.8亿 、2003年为12.88亿、2004年为12.96亿，发现两者几乎完全一致，但是当t＝2060年时用这一模型进行预测的结果远高于实际人口的 增长，误差的原因时对增长率r的估计过高。由此，可以对r是常数的假设提出疑问。实际上随着人口数量的增加，自然资源、环境因素， 人口政策，年龄和性别结构、地域特征等因素对人口 数量的阻滞作用越来越明显，增长率不应取为常数。