【论文阅读】Computing Label-Constraint Reachability in Graph Databases

Jin R, Hong H, Wang H, et al. Computing label-constraint reachability in graph databases[C]//Proceedings of the 2010 ACM SIGMOD International Conference on Management of data. 2010: 123-134.

ABSTRACT

我们今天的世界正在生成大量的图形数据，如社交网络、生物网络和语义网。许多这些真实世界的图都是带有边标记的图，也就是说，每条边都有一个标签，表示由该边连接的两个顶点之间的关系。关于这些标记图的一个基本研究问题是如何处理标签约束可达性查询：顶点u能否通过一个边缘标签被一组标签约束的路径到达顶点v？在此工作中，我们引入了一种新的基于树的索引框架，该框架利用有向最大加权生成树算法和采样技术来最大限度地压缩已标记图的广义传递闭包。在真实和合成数据集上的广泛的实验评估证明了我们的方法在回答标签约束可达性查询方面的有效性。

1. INTRODUCTION

我们今天的世界正在生成大量的图形数据，如社交网络、生物网络和语义网。如何在数据库系统中管理这些大型图已成为数据库研究界的一个重要研究课题。最基本的研究问题之一是可达性查询，它询问一个顶点是否可以到达另一个顶点。这是一个看似简单但非常困难的问题，因为这些大图的绝对大小。近年来，人们提出了许多算法来处理图的可达性查询[2,15,25,16]。
然而，许多真实世界的图都是用边标记的图，也就是说，边与标签相关联来表示顶点之间不同类型的关系。对标记图的可达性查询通常涉及到对连接两个顶点的路径的约束。在这里，我们列出了几个这样的应用程序：
Social Networks:
在一个社交网络中，每个人都被表示为一个顶点，如果两个人是相关的，那么他们就用一条边连接起来。两个人之间的关系通过不同类型的标签来表示。例如，这种关系可能包括父母、兄弟、姐妹、朋友、雇员等。许多查询在社交网络寻求发现一个人与另一个人b这些查询一般可以写好像有一个路径从B所有边的标签路径是特定类型或属于一组指定的标签。例如，如果我们想知道a是否是B的远亲，那么我们就会问是否有一条从A到B的路径，其中路径上的每个边标签都是父母的，兄弟的，姐妹的。
Bioinformatics:
理解代谢链反应如何在细胞系统中发生是系统生物学中最基本的问题之一。为了回答这些问题，生物学家利用了所谓的代谢网络，其中每个顶点代表一个化合物，两个化合物之间的有向边表明一个化合物可以通过某种化学反应转化为另一个化合物。边缘标签记录了控制反应的酶。其中一个基本问题是，两种化合物之间是否存在在一定条件下具有活性或不具有活性的途径。这种情况可以被描述为一组酶的可用性。在这里，我们的问题可以描述为可达性查询，对路径的边缘标签有一定的约束。
综上所述，这些查询会问以下问题：顶点u能否通过一个边缘标签必须满足某些约束条件的路径到达顶点v？通常，约束是成员关系：路径的边缘标签必须在约束标签集合中。或者，我们也可以要求一条避免这些标签的路径。这两种形式是等价的。我们注意到，这种类型的查询也可以在病毒式营销[19]的推荐搜索和RDF图的可达性计算中找到应用，如维基百科和YAGO [24]。
约束可达性问题比传统的不考虑任何约束的可达性查询要复杂得多。现有的关于图可达性的工作通常构造图的传递闭包矩阵的紧索引。传递闭包可以用来回答可达性的“是/否”问题，但它不能判断任意两个顶点之间是如何建立连接的。由于索引不包含标签信息，因此不能轻松地回答前面提到的标签约束可达性查询。
约束可达性问题与针对XML文档和图形的简单路径查询和正则表达式路径查询密切相关。通常，这些查询将所需的路径描述为正则表达式，然后搜索图以查看这样的路径是否存在。XPath查询是交替轴（/和//）和标签（或标签）的简单迭代，它可以通过使用正则表达式来描述两个或一个顶点[1]序列之间的路径来进行推广。我们可以将约束可达性查询视为常规简单路径查询的一种特殊示例。然而，寻找正则简单路径的一般问题已被证明是np完备的[20]。现有的处理此类查询的方法是基于等价类和细化来构建紧凑的索引，然后在这些索引[21,10]上匹配路径表达式。另一方面，针对约束可达性问题，存在一个线性算法。因此，现有的查询XML和图的工作不能有效地处理我们的约束可达性查询。

1.1 Our Contributions

在本工作中，我们详细研究了约束可达性问题，并提供了一个有效的解决方案。我们首先调查两个简单的解决方案，代表两个极端的解决方案：一个在线搜索（DFS/BFS）方法使用最少的内存，但查询回答的计算成本高，而所有成对路径信息有效地回答查询，但使用大量的内存。这里的主要研究问题是如何在这两种方法之间找到一个（好的）折衷方案。在本研究中，我们提出了一种新的基于树的索引框架，它不仅可以显著降低预计算方法的内存成本，而且能够有效地回答可达性查询。
具体来说，我们的主要贡献如下：
1.我们引入了标签约束可达性（LCR）问题，提供了两种算法来分类其计算复杂度，并推广了传递闭包（第2节）。
2.我们引入了一个新的索引框架，利用有向生成树来压缩广义传递闭包（第3节）。
3.我们研究了以最小内存代价构造索引的问题，并提出了利用有向最大加权生成树算法和采样技术来最大限度地压缩广义传递闭包的方法（第4节）。
4.我们为LCR查询提出了一种快速的查询处理方法。我们的方法建立在可达性搜索问题和几何搜索问题之间的一个有趣的联系上，允许我们利用几何搜索结构，如多维kd树或范围搜索树（第5节）。
5.我们在真实数据集和合成数据集上都进行了详细的实验。我们发现，我们的基于树的索引可以显著降低广义传递闭包的内存成本，同时仍然能够非常有效地回答查询（第6节）。

2. PROBLEM STATEMENT

数据库图（db图）是一个标记的有向图G =（V，E，Σ，λ），其中V是顶点集，E是边的集合，Σ是边标签的集合，λ是为每个边图分配一个标签λ（∈）∈Σ的函数。dbG中从顶点u到v的路径p可以描述为顶点-边交替序列，即p =（u、e1、v1、···、vi−1、ei、vi、··、en、v）。当不出现混淆时，为了简单起见，我们只使用顶点序列来描述路径p，即p =（v0，v1，···、vn）。我们使用路径标签L §来表示路径p中所有边标签的集合，即L § = {λ（e1）}∪{λ（e2）}∪···∪{λ（en）}。
定义1 Label-Constraint Reachability
给两个节点，u和v在数据库图G，和一个标签集，u，v∈V和⊆Σ，如果有一个路径p从顶点uv的路径标签L §的一个子集，即L §⊆，那么我们说你可以达到v与标签约束，表示为（u−→v），或者简单的v是可实现的。我们也把路径p称为从u到v的a路径。给定两个顶点u和v，以及一个标签集A，标签约束可达性（LCR）查询询问v是否可以从u到达。
在本文中，我们将使用图1作为一个运行示例，使用整数来表示顶点，使用字母来表示边缘标签。在这个例子中，我们可以看到顶点0可以通过标签约束{a，b，c}到达顶点9。换句话说，顶点9是可以从顶点0可以到达的。此外，路径（0、3、6、9）是从顶点0到9的{a、b、c}-路径。

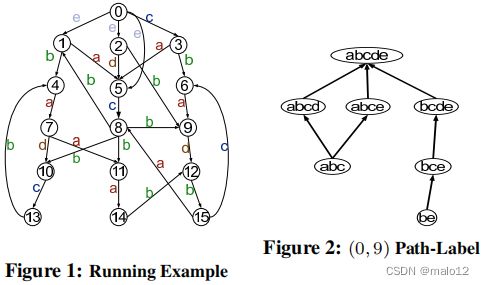
下面，我们将讨论回答标签约束可达性（LCR）查询的两种基本方法。

2.1 Online DFS/BFS Search

回答一个LCR查询的最直接的方法是在线搜索。我们可以应用DFS（深度优先搜索）或BFS（宽度优先搜索），以及标签约束，来减少搜索空间。让我们考虑从顶点u到v的a-可达查询的DFS。为简单起见，我们说一个顶点x是相邻顶点u，如果有一个边e连接你x，例如，e =（u，x）和e的边缘标签包含在，λ(e)∈a从顶点u，我们递归地访问所有的顶点，直到我们到达顶点v或搜索所有可到达的顶点从u没有到达v。显然，在O（|V | + |E|）中，我们可以得出结论，v是a是否可以从u到达的。因此，回答标签约束的可达性查询可以在多项式时间内完成。但是，由于数据库图的大小非常大（它可以很容易地包含数百万个顶点），因此这种简单的在线搜索对于图数据库中的快速查询回答是不可接受的。
我们可以通过一个更“集中”的搜索程序来加速这种在线搜索。加速是基于观察到的，在上述过程中，我们可以从顶点u访问许多顶点，无论我们走什么路径，它们都不能到达顶点v。为了避免这种情况，我们可以利用可达性查询[2,15,25,16]的现有工作，它告诉一个顶点是否可以很快到达另一个顶点。因此，当我们试图从当前的顶点访问一个新的顶点，记为u‘时，我们要求这个顶点不仅与u’相邻，而且还可以到达目标顶点v（利用传统的可达性指数）。请注意，BFS过程也可以以类似的方式进行扩展。

2.2 Generalized Transitive Closure

另一种方法是预先计算路径标签集，即在任意两个顶点之间的所有路径标签。请注意，这对应于可达性查询的传递闭包。路径标签集的主要差异性是空间成本。在任意两个顶点之间的所有路径标签的数量的上界是2 |Σ|。
因此，总的存储复杂度为O（|V |2 2 |Σ|），代价过于高。
然而，为了回答标签约束可达性（LCR）查询，我们通常只需要记录一小部分路径标签。直觉是，如果顶点u可以到达顶点v标签约束，那么你可以达到任何标签约束a‘⊇。换句话说，我们总是可以把路径标签从uv的超集路径标签从uv不影响LCR查询结果的正确性。例如，在我们从顶点0到9的运行示例中，我们有一个路径（0、2、9），它有路径标签{b、d}，以及另一个路径（0、2、5、8、9），它有路径标签{b、d、e、a}。然后，对于任何标签约束A，我们将不需要检查第二个路径来回答查询。
为了正式引入这样的约简，我们需要考虑哪一组路径标签就足以回答LCR查询。
定义2 Sufficient Path-Label Set 设S是从顶点u到v的一组路径标签。然后，我们说S是一个足够的路径标签集，如果对于任何标签约束a，u→av，LCR查询返回true，如果有一个路径标签s∈S，这样的⊆a。
显然，从顶点u到v的所有路径标签的集合，记为s0，就足够了。我们的问题是如何找到包含最小路径标签数的最小充分路径标签集。这个集合可以在定理1中精确地描述。
定理1。设s0是从顶点u到v的所有路径标签的集合。从u到v的最小充分路径标签集，称为Smin，是唯一的，只包括那些在s0中没有任何（严格的）子集的路径标签，即，
Smin = {L §|L §∈S0∧∃L（p‘）∈S0，这样，L（p’）⊂L §}换句话说，对于任意两个路径标签，Smin中的s1和s2，我们有s1 6⊂2和s2 6⊂1。
这个定理清楚地表明，我们可以在S中删除包含另一个路径标签集的所有路径标签集，而不影响LCR查询的正确性。为了简单起见，我们省略了它的证明。此外，我们还可以利用部分阶集（偏序集）来描述最小充分路径标签集。设子集（⊆）关系为s0上的二进制关系“≤”，即L1≤L2 iff L1⊆L2（L1，L2∈S0）。然后，最小充分路径标签集是s0的下界，并且仅由所有和最小元素[3]组成。图2显示了使用Hasse图从顶点0到9的所有路径标签集。我们可以看到它的最小充分路径标签集只包含两个元素：{b、e}和{a、b、c}。任何最小充分路径标签集的基数的上界是`|Σ||Σ|/2‘。这也相当于Σ的幂集中非可比元素的最大数量。这个界可以很容易地观察到，在组合学中通常被称为斯珀纳定理[3]。
算法描述：我们提出了一种有效的算法来构造给定图中所有顶点对的最小充分路径标签集，使用动态规划方法对应于最短路径和传递闭包[8])。
设Mk（u，v）表示从u到v的中间路径在{v1、···、vk}中的最小充分路径标签集。现在我们考虑如何计算从每个顶点u到v的路径的最小充分路径标签集，从中间顶点到vk+1，即Mk+1（u，v）。注意，Mk+1（u，v）描述了两种类型的路径，第一种类型是只使用中间顶点（v1，···，vk）的路径，第二种类型是通过中间顶点到vk+1的路径。换句话说，第二种类型可以描述为由两种路径组成的路径片段，首先从u到k + 1，然后从k + 1到j。鉴于此，我们可以通过以下公式递归地使用这两种路径计算最小充分路径标签集：

在这里，Prune是一个函数，它可以简单地删除所有的路径标签，这些路径标签是输入集中其他路径标签的超集。换句话说，Prune将产生输入路径标签集的下界。⊙操作符连接两组集合，如{s1s2}⊙{s‘1s’2s‘3}={s1∪’1s1∪‘2···s2∪’3}，其中si和s‘j是标签集。此外，我们还可以很容易地观察到这一点

其中S1和S2是两个路径标签集。Mk+1（u，v）的递归公式的正确性自然遵循这两个方程。
算法1描述了动态规划过程，该过程为图g中的所有顶点对构造最小充分路径标签集。对于这个动态过程，最坏情况的计算复杂度是Ov32e，内存复杂度是ov2ee2.

3. A TREE-BASED INDEX FRAMEWORK

第一节中的两种方法，在线搜索和广义传递闭包计算，代表两个极端的标签约束可达性（LCR）查询处理：第一种方法的内存成本最低索引但非常高的计算成本回答查询，而第二种方法的内存成本很高，但很低的计算成本回答查询。因此，我们在这项工作中要解决的主要研究问题是如何设计一种具有低内存成本但仍然可以有效地处理LCR查询的索引机制。
我们的方法的基本思想是利用生成树来压缩广义传递闭包，它记录了db图中任意对顶点之间的最小充分路径标签集。虽然生成树已被应用于有向无环图（DAG）来压缩传统的传递闭包[2]，但我们的问题非常不同，也更具挑战性。首先，db图和LCR查询都包含了传统可达性索引无法处理的边缘标签。其次，我们问题中的db图是一个有向图，而不是一个DAG。我们不能通过将强连接的组件合并成单个顶点来将有向图转换为DAG，因为在这些组件中表示了更多的路径标签信息。最后，复杂性由标签组合产生的，即路径-标签集，比任何两个顶点之间的基本可达性高出一个数量级。应对这样的复杂性是非常具有挑战性的。
为了处理这些问题，我们的索引框架包括两个重要的部分：一个db图的生成树（或森林），记为T，和一个部分传递闭包，记为NT，用于回答LCR查询。在高级上，这两部分的组合包含足够的信息来恢复完全的广义传递闭包。然而，这两部分所要求的总指数大小比完全的广义传递闭包要小得多。此外，LCR查询处理可以非常有效地实现，它包括遍历生成树结构和对部分传递闭包的搜索。
设G（V、E、Σ、λ）是一个db图。设T（V，ET，Σ，λ）是db图的一个有向生成树（森林），其中ET⊆E.注意，我们可能无法找到一个生成树，相反，我们可能会找到一个生成森林。在这种情况下，我们总是可以通过创建一个虚拟根来将树连接到生成林中的根来构造生成树。因此，我们不会区分跨越树和跨越森林。为简单起见，我们总是假设有一个虚拟根。为了方便起见，我们说边∈是树边，∈中的边而不是∈中的边是非树边。g有许多可能的生成树。图3显示了我们运行的示例图（图1）的一个生成树，其中粗体线突出显示了生成树中的边，虚线是图中的非树边。

为了利用db图G的生成树结构T来压缩广义传递闭包，我们正式地引入了任意两个节点之间的路径分类。
定义3。（路径分类）考虑一个db图G及其生成树t。对于G中的一个路径p =（v0、e1、v1、··、en、vn），我们根据其起始边（e1）和结束边（en）将其分为三种类型：1。（Ps）包含其起始边为树边的所有路径，即e1∈ET；2。（Pe）包含最后一条边是树边的所有路径，即en∈ET；3。（Pn）包含了起始边和结束边都是非树边的所有路径，即e1，en∈E\ET。
我们还将第三种类型的路径Pn称为非树形路径。另外，如果路径p中的所有边都是树边，即1≤≤的ei∈ET，那么，我们将其称为树内路径。
请注意，一条路径（如果它以树边开始，以树边结束）可以同时属于第一种和第二种类型的路径。事实上，树内路径就是这样一个例子，它是Ps和Pe路径的特殊情况。在我们的运行示例中（图3）中，路径（0、2、9、12)是从顶点0到12的路径内路径（0、2、5、8、11、14、12）是Ps的示例，路径（0、5、8、11、14、12）是非树形路径Pn，而路径（0、5、8、9、12）是第二路径类型Pe的示例。
现在，我们进一步介绍了路径标签集的分类，特别是携带基本的非树状路径标签的部分传递闭包。
定义4。（部分传递闭包）设M（u，v）是g中从顶点u到v的最小充分路径标签集。设p是从顶点u到v的路径。然后我们根据路径类型1定义M（u，v）的三个子集：1。Ms (u, v) = {L §|p ∈ Ps} ∩ M (u, v); 2.我（u，v）= {L §|p∈Pe}∩M（u，v）；3。NT（u，v）= {L §|p∈Pn}∩M（u，v）−Ms（u，v）−Me（u，v）；部分传递闭包NT记录所有的NT（u，v），（u，v）∈V×V，其中NT（u，v）=∅。
很明显，这三个子集的并集是从u到v的最小充分路径标签集，即，M（u，v）=Ms（u，v）∪Me（u，v）∪NT（u，v）。此外，Ms（u，v）∩Me（u，v）可能不是空的，而是（Ms（u，v）∪Me（u，v））∩NT（u，v）=∅。定理2如下状态，我们只需要记录部分传递闭包（NT）结合生成树T为了恢复完整的传递闭包m。因此，它奠定了我们的索引框架的理论基础：T和NT一起记录足够的信息LCR查询处理。图4显示了我们运行的运行示例中的生成树的NT（图3）。在这里，NT总共只有26个条目，即非空的（u，v）的数量，NT（u，v）=∅，并且每个条目目的基数（路径标签的数量）是1。在这些非空条目中，有12个只是原始图中的边。因此，只需要额外的14个条目记录NT来恢复完整的传递闭包M。注意，我们运行的示例图总共有16个顶点和29条边，M的大小为210，P（u，v）∈V×V|M（u，v）|=210。
定理2。（重构定理： T+NT→M（u，v））给定一个db图G和一个G的生成树T，设NT为定义4中定义的部分传递闭包。设Succ (u)是树t中u的所有后继者。设P红(v)是树t中v的所有前身。此外，u‘∈Succ (u)和v’∈P red (v)。然后，我们可以用T和NT构造从u到v的路径标签集的M‘（u，v），如下所示：

其中，对于任意顶点x，L（PT（x、x））= L（PN（x、x））=∅和NT（x、x）={∅}。然后我们有，对于任何顶点u和v，M（u，v）⊆M‘（u，v），和M（u，v）=Prune（M’（u，v））。
由于空间的限制，我们在这里省略了证明。有兴趣的读者可以详细参阅我们的技术报告[14]。
为了将这个定理应用于索引构建和LCR查询处理，我们需要解决以下两个关键的研究问题： 1)不同的生成树T可以有非常不同大小的部分传递闭包NT。我们如何找到一个最优的生成树T来最小化总索引的大小，特别是部分传递闭包NT的代价？2)如何利用生成树T和部分传递闭包NT来有效地回答LCR查询？这不是一个简单的问题，一个好的查询处理方案可以像我们直接查询完整的广义传递闭包一样快，但内存成本要小得多。我们将研究第4节中的第一个问题（最优索引构造）和第5节中的第二个问题（有效的LCR查询处理）。

4. OPTIMAL INDEX CONSTRUCTION

在本节中，我们将研究如何构造一个最优生成树T来最小化部分传递闭包NT的代价，这是我们整个索引框架的主要代价。在第4.1小节中，我们将介绍一种基于最大有向生成树算法[7,9]的有趣的方法来解决这个问题。然而，这个解决方案依赖于广义传递闭包m的完全物化。虽然这可以使用标签传递闭包算法（第2.2小节中的算法1）来完成，但当图的大小变大时，它会变得非常昂贵（对于计算和存储）。在第4.2小节中，我们提出了一种新的近似算法，它可以与精确的最大生成树相比，同时找到具有有界代价差的生成树。

4.1 Directed Maximal Spanning Tree for Generalized Transitive Closure Compression

设M为广义传递闭包，它包含任意两个顶点u和v之间的最小充分路径标签集。回想一下，对于生成树T，NT（u，v）= M（u，v）−Ms（u，v）−Me（u，v）记录了非树路径的“基本”路径标签，这些路径不能被类型的Ps路径（从树边开始）或Pe路径（以树边结束）所取代。有鉴于此，部分传递闭包NT的大小可以正式定义为

然而，直接最小化成本（NT）是困难的，这个优化问题的复杂性仍然是开放的。为了解决这个问题，我们考虑了一个相关的部分传递闭包MT，它的代价f (T)作为代价（NT）的上界：
定义5。给定db图G及其生成树T，对于G中的任何顶点u和v，我们定义MT（u，v）为M（u，v）的一个子集，其中包括从u到v的路径的路径标签，这些路径以一个非树边结束。正式地，

现在我们介绍了广义传递闭包m的MT、NT和m的其他子集（Ms和Me）之间的几个基本方程。这些表达式不仅有助于我们有效地计算它们，而且有助于我们发现最优生成树。
引理1。给定db图G及其生成树T，对于G中的任意两个顶点u和v，我们有以下等价性：

由于空间的限制，我们在这里省略了证明。有兴趣的读者可以详细参阅我们的技术报告[14]。显然，这个新的部分传递闭包MT的大小不小于我们的目标部分传递闭包NT（MT（u，v）⊇NT（u，v））的大小。现在，我们将重点关注以下的优化问题。
定义6。（NT大小的上界及其优化问题）给定db图G及其生成树T，设新的目标函数f (T)为MT的代价，即，

给定db图G，优化问题是如何找到G的最优生成树到，从而使f (T) =代价（MT）最小化：

由于cost（NT）≤f (T)，我们也将f (T)称为成本（NT）的上限。我们将通过三个步骤将其转化为最大有向生成树问题：
步骤1（权重分配）：对于db图G中的每条边（v‘，v）∈E (G)，我们将其与权重w（v’，v）关联起来：

请注意，这个权重直接对应于M（u，v）中的路径标签的数量，它可以通过边（v‘，v）到达v。特别是，如果我们在生成树中选择了这条边，那么，我们就有了

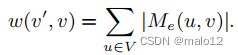
因此，这个权值（v‘，v）也反映了如果它在树中，我们可以从所有以顶点v结束的路径标签集中删除的路径标签的数量，以生成新的部分传递闭包

图5显示了我们的运行示例中与公式4中定义的权重相关联的每条边。例如，edge（1,5）有一个权重13，这表明如果我们将该边纳入生成树中，那么，我们可以从这些路径标签集中保存13个路径标签，即Pu∈V|M（u，5）−MT（u，5）| = 13。

步骤2（发现最大有向生成树）：鉴于此，G的最大有向生成树定义为有根有向生成树T =（V，ET）[7,9]，其中ET是E的子集，使ET中所有（u，v）的w（u，v）的和最大化：

其中，W (T)为生成树的总权重。我们可以调用Chu-Liu/Edmonds算法[7,9]来寻找G的最大有向生成树。
定理3。G的最大有向生成树T‘将使新的部分传递闭包MTf(T)最小化，这也是NT大小的上界：

证明草图：为了证明这一点，我们将展示新的部分传递闭包大小MT、f (T)与有向生成树的总体权值之间的重要等价关系

设完全广义传递闭包M的大小M为

然后，对于G的任何生成树T，以下条件成立：

由于cost (M)是db图G的一个常数，这个方程表明f (T)的最小化等价于W (T)的最大化。我们证明了这个方程如下： f (T) =

最后，一旦确定了最优生成树T，我们就可以计算出部分传递闭包NT如下。
步骤3（部分传递闭合NT）：根据引理1从M和T中计算NT。我们的索引构造过程（步骤1-3）的总计算复杂度是O（|V | 2 2 2|Σ|），因为第一步需要O（|V |（2|Σ|）2），第二步需要O（|E|+|V|日志|V||），最后一步需要O（|V | 2（2|Σ|）2）在最坏情况下的时间。

4.2 Scalable Index Construction

上述索引构造算法依赖于广义传递闭包M的预先计算，这对于大图来说太昂贵了。特别是，M的存储成本很容易超过主存的大小，导致内存抖动。使我们的索引建设可扩展到大型图表，我们必须避免完整的物化m.注意最大生成树算法的目标是优化树的总权重P（u，v）∈Tw（u，v），这对应于NT的下界。这里的研究问题是，我们如何发现一个总权值接近于具有保证概率界的最大生成树的总权值的生成树。具体地说，我们将近似最大生成树问题表述如下：
定义7。（近似最大生成树问题）给定一个db图G，设为G的最优生成树，它具有最大的总权值W（To）=P（v‘，v）∈ETow（u，v）。近似最大生成树问题试图找到G的另一个生成树T，当概率至少为1−δ时，其总权重W (T)与最大树权重W（To）的相对差不大于θ：

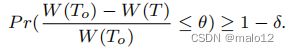
在这个问题中，o和δ都是用户定义的参数，以指定近似最大生成树的优度。例如，如果o=为1%，δ=为0.1%，则概率为99.9%，期望树T的总权值不小于精确最大生成树的总权值的99%，即W (T)≥99%W（至）。请注意，近似生成树的总权重不能超过W（To）。
下面，我们提出了一种新的算法，通过采样来解决这个问题，从而避免了大图的广义传递闭包M的完全物化。简而言之，我们的算法的工作原理如下：
步骤1：我们首先采样db图G中的一个顶点列表。
步骤2：然后我们计算它们在G中的每个广义传递闭包，即，对于一个样本顶点u，我们计算图中每个顶点v的M（u，v）。后者被称为单源传递闭包问题，可以有效地解决。
步骤3：我们使用来自这些样本顶点的单源M (u、v）来估计精确的边权重(w（v’、v）、公式(4)）和误差界限（置信区间）。具体地说，我们利用霍夫丁和伯恩斯坦界进行误差界估计。鉴于此，每条边都与两个值相关联，一个为估计的权重，另一个为误差界。
步骤4：我们在db图G中发现两个最大生成树作为边权分配。
步骤5：我们引入了一个简单的测试条件，使用这两棵树的总权值来确定是否满足准则(5)。如果答案是否定的，我们将重复上述步骤，直到测试条件成立为止。我们将此算法称为霍夫丁-伯恩斯坦树，因为它利用霍夫丁和伯恩斯坦边界[11,22]来确定停止条件。
具有霍夫丁和伯恩斯坦边界的抽样估计器。回忆边缘重量

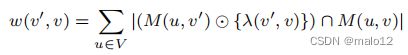
在我们的算法中，一个重要的成分是利用抽样和统计边界（霍夫丁和伯恩斯坦边界）来提供对图中每个边的权值的准确估计。对于w（v‘，v）的基于抽样的估计器的关键观察结果是，w（v’，v）是|V |单个量，|（M（u，v‘）⊙{λ（v’，v）}）∩M（u，v）|的和。这就产生了这个问题：假设我们有n个样本u1、u2、···、un，并且对于每个样本顶点ui，我们能否有效地计算每个单独的项

在这里，我们利用抽样和替换来简化统计推断。为了方便起见，我们还关注于近似这个数量：

请注意，由于每个边权（和误差）除以相同的常数|V |，（总）边权的相对差的界限保持不变。实际上，我们可以把原始的w（v‘，v）看作是总体和，新的量Xe是总体平均值，其中一个量u在总体中的权重是|（M（u，v’）⊙{λ（v‘，v）}）∩M（u，v）|。
鉴于此，我们将Xe的抽样估计量定义为

注意，对于每个样本Xi，E（Xe，i）= Xe和Xi都是一个有界的随机变量，即Xi∈[0，R]，其中R=`|Σ||Σ|/2‘。
正如我们前面提到的，在采样过程中，每条边e都保持有两个值，一个是估计的边权值ˆXe，n，另一个是误差界oe，n。利用经典的霍夫丁不等式[12]，得出了经验结果的偏差（误差界）来自真实期望（Xe）的平均值为：概率至少为1个−δ‘，

然而，这个界限是相当松散的，因为它根据n而减小。最近，通过加入经验的伯恩斯坦界[11,22]，霍夫丁界得到了改进，它只依赖于经验标准差：

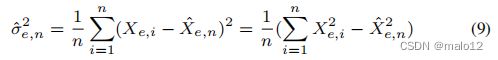
霍夫丁和伯恩斯坦的结合界表示为：

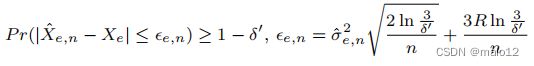
在这里，误差项oe，n中的范围R的依赖性相对于样本量n呈线性减小。误差项也取决于ˆσ2√e，nn。然而，由于经验标准差ˆσ2e，n通常比范围R小得多，这个界比霍夫丁界更紧。在我们的算法中，我们使用霍夫丁界和伯恩斯坦界（10）作为我们的误差界。请注意，估计的边权值ˆXe，n和误差界oe，n都可以很容易地进行增量维护（不记录每个样本ui和边e的Xe，i）。我们只需记录以下两个样本统计数据，Pn i=1 Xe，i和Pn i=1 X 2 e，i。对于误差界的确定（10），我们需要选择δ‘，在我们的算法中被指定为δ’=δ|E，得到以下观察结果：
引理2。给定n个样本顶点和δ‘=δ|E|，其概率大于1−δ，图中每个估计的边权值ˆXe，n与它们的精确边权值Xe的偏差不大于（10）中定义的误差界：

这可以很容易地用邦费罗尼不等式来证明。引理2也提出了一个计算程序来估计每个边的权值。基本上，假设我们有n个样本，u1，u2，···，un，对于每个样本顶点ui，我们将计算任何顶点v∈v的单源广义传递闭包，M（ui，v）。从那里，我们可以计算出图中每条边e的Xe，i。
近似的最大生成树的构造。假设我们有n个样本顶点，上面的讨论描述了图中的每条边都与两个值相关联，估计的权重ˆXe，n及其误差界oe，n。在此基础上，我们的算法将在db图G中发现两个最大生成树，树T为估计的边权值ˆXe，n赋值，树T‘为误差界oe，n赋值。在什么条件下，我们能判断树T是满足标准(5)期望的树？定理4为这个问题提供了一个肯定的答案。
定理4。给定n个样本，设T为G的最大生成树，其中每条边e的权值为ˆXe，n，设T‘为G的最大生成树，其中每条边的权值为oe，n。我们表示Wn(T)=Pe∈TˆXe，n和∆n（T‘）=Pe’∈T‘oe’，n。那么，如果T满足（12），那么T是我们的近似树：


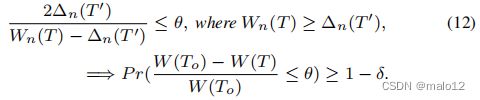
总体算法。在算法2中说明了赫夫丁-伯恩斯坦树算法的示意图。该算法以批处理的方式执行。在每个批处理中，我们采样n个0个顶点。第3−4对应于采样步骤（步骤1），第5−11描述了每个采样顶点的单源传递闭包计算（步骤2），第12−15计算每条边的两个值、估计的边权重及其误差界（步骤3），第16和第17行找到边值的最大生成树（步骤4），最后，第18行测试这两个树是否满足公式（12）中描述的条件。批量采样减少了对MST（定向最大生成树算法）的调用。批样本量n0是可调的，不影响该算法的正确性。对于非常大的图G，我们通常设置n0 = 100。稍后我们将在实验结果中展示，由于最大生成树算法的计算成本相对便宜，n0的选择不会显著影响运行时间。
单一源路径标签方法用于计算来自单个顶点u的推广传递闭包。这个过程本质上是对著名的贝尔曼-福特算法的推广[8]。这个过程以一种迭代的方式工作。在集合V1中，我们记录了当前迭代中其路径标签集已被更改的所有顶点（第25行、−第26行和第30行）。然后在下一个迭代中，我们访问V1中顶点的所有直接邻居，并相应地修改它们的路径标签集（行22−29）。对于单个源的计算，V1被初始化为只包含单个顶点u。此过程将继续进行，直到任何路径标签集（V1 =∅）没有发生更改为止。考虑到u能到达的最长路径顶点u为|V |步长，很容易看出最大迭代次数为|V |。因此，单源路径标签的最坏情况计算复杂度为Oveee2.
鉴于此，我们可以看到霍夫丁-伯恩斯坦树的总计算复杂度为Onveee2+nn0e+vlogv。
第一项来自于单源广义传递闭包计算，第二项来自于最大生成树算法。显然，第一项是主导部分。然而，由于样本量通常相当小（正如我们将在实验评估中显示的那样），霍夫丁-伯恩斯坦树算法非常快。此外，该算法的内存要求非常低，因为我们只需要暂时存储单个顶点的单一源路径标签的中间结果。我们注意到，当总标签尺寸|Σ|很小时，该算法可以很好地工作。由于采样误差的界限是在线性顺序上的e2，当不同标签的数量很大时，采样大小很容易超过图中的顶点总数。在这种情况下，我们可以简单地计算图中每个顶点的单个源路径标签集，然后保持Pn i=1 Xe，i，而不是采样。因此，在这两种情况下，我们都可以完全消除由于生成生成树的广义传递闭包M的完全物化而导致的内存瓶颈。
最后，我们注意到，在派生生成树T后，我们需要计算部分传递闭包NT。在原始索引构造（第4.1小节）的第3步中，我们依赖于引理1，仍然需要广义传递闭包m。在下面的过程中，我们描述了一个简单的过程，它可以计算单源部分传递闭包，即每个v∈v的顶点u的NT（u，v）。这个想法类似于前面提到的单源路径标签算法。然而，我们不会为u中的每个顶点v只维护一个路径标签集，在单源路径标签中表示为M[v]（对应的M（u，v）），而是基于定义4： 1) Ms[v]对应于Ms（u，v），它记录了u中的所有路径标签到v，第一个边是树边；2) Me[v]，对应于Me（u，v）−Ms（u，v），记录从u到v的所有路径标签，最后一条边为树边，第一个边为非树边；3) NT[v]对应NT（u，v），记录从u到v的路径标签，第一条边和最后一条边都是非树边。请注意，由于每个集合都是由路径中的第一个和/或最后一个边类型唯一定义的，所以我们可以在计算单源路径标签算法时很容易地维护它们。基本上，我们可以依次计算每个顶点的NT，并且它的计算复杂度与单一来源的路径标签算法的计算复杂度相同。由于空间的限制，我们在这里省略了一些细节。

5. FAST QUERY PROCESSING

在本节中，我们将研究如何使用生成树T和部分传递闭包NT来有效地回答LCR查询。使用定理2，我们可以很容易地推导出以下过程来回答LCR查询（u−→v）： 1)我们对根于u的子树进行DFS遍历，以找到u‘∈Succ (u)，其中L（PT（u，u’）⊆A）；2)对于给定的u‘，我们在部分传递闭包中检查它的每个邻居v’，即NT（u‘，v’）=∅和v‘∈P red (v)，看看NT（u’，v‘）是否包含一个路径标签，它是a的子集；和3)对于那些v’，我们检查L（PT（v‘，v））⊆A。换句话说，我们试图识别一个路径标签，它是a的一个子集，由三个部分表示，开始树内路径标签L (PT（u，u’）），非树部分NT (u’，v’）和结束树内部分L（PT（v’，v））。
然而，这个过程是低效率低下的，因为部分传递闭包非常稀疏，而且u的许多后继者没有通过NT链接到任何v的前任。此外，u的继承集的规模可以非常大。这就引出了以下问题：我们能否快速识别出所有的（u‘，v’），其中u‘∈Succ (u)和v’∈P红色(v)，这样NT（u‘，v’）=∅？我们需要解决的第二个重要问题是如何有效地计算树内的路径标签，L (PT (u，u’））和L（PT（v’，v））。这是LCR查询的查询处理的关键操作，我们显然不想遍历树内路径从起始顶点，如u，到结束顶点，如u‘，来构造路径标签。如果我们能积极地回答这两个问题，我们如何利用它们来为LCR查询设计一个有效的查询回答程序呢？我们将在以下几个小节中研究这些问题。

5.1 Searching Non-Empty Entry of NT

在本小节中，我们将推出一个有效的算法利用多维几何搜索结构快速识别非空条目的部分传递关闭：即，给定两个顶点u和v，快速识别所有的顶点对（u，v），u‘∈Succ (u)和v’∈Pred(v)，这样NT（u，v）=∅。
解决这个问题的直接方法是首先找到所有u的后继者（Succ (u)）和v的前身（Pred(v)），然后测试每对笛卡尔积Succ(u)×Pred(v)，看看NT中相应的条目是否为空。该方法具有O（|Succ (u)|×|P red (v)|）的复杂度，明显过高。
我们的新方法利用生成树t的区间标记方案[10]。我们对树进行预定序遍历，以确定每个顶点的序列号。树中的每个顶点u都被分配了一个间隔：[pre (u)，索引(u)]，其中pre (u)是u的预定数，索引(u)是u的后继者的最高预定数。图6显示了图3中生成树的间隔标记。很容易看出，顶点u是顶点v iff [pre (v)，索引(v)]⊆[pre (u)，索引(u)] [10]的前身。
我们的新方法的关键思想是利用生成树将这个搜索问题转化为一个几何范围搜索问题。简单地说，我们将NT的每个非空条目（u‘，v’）映射到一个四维点中，并将查询顶点u和v转换为一个轴平行的范围。我们用下面的定理来描述我们的变换及其正确性。
定理5。让每一对（u‘，v’），其中NT（u‘，v’））=∅被映射到一个四维点（前（u‘)、索引（u’）、pre（v‘）、索引（u’））。然后，对于任意两个查询顶点u和v，顶点对（u‘、v’）、u‘∈Succ (u)和v’∈P红色(v)，使得NT（u‘、v’）=∅对应于四维空间的四维点（前(u)、索引(u)、前(v)、指数(v)）范围：（[前(u)、索引(u)]、[前(u)、索引(u)]、[1、前(v)]、[索引(v)、|V|）。
由于空间的限制，我们在这里省略了证明。有兴趣的读者可以详细参阅我们的技术报告[14]。

图7给出了每个NT (u、v）的4-D坐标（前(u)、索引(u)、前(v)、索引(v)）。例如，考虑在图G上的一个查询（u，v），生成树如图6所示，其中u = 11和v = 6。有一个顶点对（u‘，v’），其中NT（u‘，v’）={c}和u‘=14和v’=12，这样的u‘∈Succ (u)和v’∈Succ (v)。易于验证（前(u)、指数(u)、前(v)、指数(v)、（14、14、4）、指数(u)、[前(u)、指数(u)、[1、前(v)、15）。
这种转换允许我们同时对u的后继者和v的前身应用测试条件，并且这些测试条件对应于多维范围搜索。使用kd树或范围搜索树，我们可以有效地索引和搜索一个轴平行范围[5]中的所有点。具体来说，kd-tree的构造需要O（n log2 n），在平衡的kd树中查询轴平行范围需要O（n 3/4 + k）时间（在四维空间中），其中n是NT中非空条目对的总数，k是报告点的数量。范围搜索树提供了更快的搜索时间。它可以在O（n log3 d）时间内构造，并以O（log4 n + k）时间（对于四维空间）回答查询。

5.2 Computing In-Tree Path-Labels

在本小节中，我们提出了一种基于直方图的技术来快速计算树内路径的路径标签。设x和y是树T中的两个顶点，其中x是y的祖先，x∈P红色(y)。我们的目标是非常快地计算出从x到y，L（PT（x，y））的树内路径的路径标签集。我们为树t中的每个顶点建立一个直方图。让r是t的根顶点，然后，顶点u的直方图，记为H (u)，不仅记录内树路径中的每个唯一标签，即L（PT（r，u）），还记录包含每个标签的路径中的边数。例如，图3中顶点14的直方图为H（14）= {b： 1、d： 2、e： 2}，顶点6的直方图为H (6) = {a： 2、b： 2、c： 1、d： 1、e： 1}。显然，一个简单的DFS遍历过程可以为O（|V ||Σ|）中T的每个顶点构造T的直方图。
我们可以通过从H (v)中减去H (u)中相应的计数器来计算从顶点u到v的路径标签集。具体来说，对于H (v)中的每个边标签，如果它存在，我们将用H (u)中的相同标签的计数器减去H (v)中的计数器。如果相同标签的计数器没有出现在H (u)中，我们将该计数器视为0。鉴于此，从u到v的路径标签集包括所有结果计数器大于0的标签，也就是说，我们知道在从u到v的树内路径上有一条带有这个标签的边。显然，这种方法利用O（|V ||Σ|）存储和可以计算一个树内路径标签在O（|Σ|）时间，|Σ|不同的标签树t因为可能的标签，|Σ|，通常很小，可以视为一个常数，这种方法可以计算任何路径标签路径非常快。

5.3 LCR Query Processing

在此，我们提出了一种新的快速LCR查询处理算法，该算法利用新技术有效地搜索NT中的非空条目的条目。该算法的示意图见算法3。对于一个LCR查询（uA→v），在第一步（第1行）中，我们搜索所有的顶点对（u‘，v’），其中u‘∈Succ (u)和v’∈P red (v)，这样NT（u‘，v’）=∅。我们可以通过将这一步转化为一个几何搜索问题，然后利用kd-树或距离搜索树来检索所有的目标对，从而非常有效地实现这一点。我们把所有这些对放在一个列表L中。然后，我们测试L中的每个顶点对（u‘，v’），看看我们是否可以使用这三个段，PT（u，u‘），NT（u’，v‘）和PT（v’，v）来构建一个路径标签。在这里，树内的路径标签是使用基于直方图的方法来计算的。因此，我们首先测试内树路径标签集L(PT（u，u）和L（PT（v，v））是否是A的子集，然后检查NT（u、v）是否包含一个路径标签集，它是A的子集。
我们积极地修剪那些不能用标签约束a连接u和v的（u‘，v’）对。这是在第10行和第13行中完成的。注意，当L（PT（u，u‘））不是A的子集时，我们知道Succ（u’）中的任何顶点（即树T中u‘的任何后继者）都不能通过树内路径从u中到达。类似地，当L（PT（v‘，v））不是A的子集时，我们可以推断Pred（v’）中的任何顶点（即树T中v‘的任何前身）使用树内路径在标签约束A的情况下不会到达v。因此，我们可以从列表L中删除这些对。

该过程的计算复杂度为O（logn + Pk i=1 |NT（ui，vi）|），其中n是NT中非空条目的总数，k是得到的NT的非空对，其中从第一步开始，列出为（ui、vi）。我们进一步假设树内路径标签集可以在恒定的时间内计算，因为可能的标签的数量是固定的，而且通常很小。

6. EXPERIMENTS

在本节中，我们将对真实数据和合成数据集进行详细的实验研究。具体来说，我们感兴趣的是了解本工作中提出的五种方法的索引大小、查询时间和索引构建时间之间的权衡：1)在线深度优先搜索（第2.1小节中的DFS）；2)聚焦深度优先搜索（第2.1小节中的聚焦DFS）；3)使用广义Floyd-Warshall(第2.2小节中的算法1），4）最优生成树（选择闭包后构造的完整广义传递闭包（第4.1小节）；5）霍夫丁-伯恩斯坦树（第4小节中的算法2。2)，在本节中称为采样树。在我们的框架中，我们使用多维几何数据结构kd-tree来搜索NT的非空整数。所有这些算法都是使用C++实现的，我们的实验都是在一个具有6GB内存的2.0 GHz双核AMD Opteron（tm）上进行的。

6.1 Setup on Synthetic Datasets

我们在五组实验中使用了一组合成数据集，来研究回答LCR查询的五种方法的几个不同方面。合成数据集分两步生成。首先，我们生成两种类型的随机有向图，一种基于erdo-renyi（ER）模型[17]，另一种基于无标度（SF）模型[4]。其次，我们在这些生成的随机图中分配一个与每条边相关联的随机标签。标签的分布是根据幂律分布生成的，以模拟只有少数标签出现得相当频繁，而大多数标签出现得很少的现象。
Expr1.a（ER图上的变化密度）：在第一组实验中，我们研究了索引大小、查询时间和索引构建时间如何随边缘密度而变化。我们确定了顶点的数量|V | = 5000。然后我们根据ER模型将密度|E| |V |范围从1.5到5。
Expr1。b（ER图上改变查询约束大小）：我们修复|V | = 5000，密度|||V|=1.5，然后根据ER模型将查询标签约束||从总边缘标签的15%改为85%。
Expr1。c（ER图的可扩展性）：我们对密度为|||V|=1.5的图进行实验，然后将图大小|V |从20,000改变到100,000。
Expr1。d（在SF图上改变查询约束大小）：我们修复了|V | = 5000，并基于RMAT算法[6]生成无标度图，然后将查询标签约束|A|从总边缘标签的15%更改为85%。
Expr1。e（SF图上的可伸缩性）：我们对基于RMAT算法的无标度图进行可伸缩性实验，通过从20000改变图的大小|V |到100000。
此外，对于每个随机生成的图，我们将可能的边缘标签（|Σ|）的总数设置为20。在Expr1.a和Expr1.c中，我们将查询标签集|A|固定为总边标签数|Σ|的30%。同时，我们还设置了幂律分布参数α = 2 [23]。此外，对于抽样树，我们设置了相对误差界θ = 1%和用户置信水平参数δ = 1%。

6.2 Results on Synthetic Datasets

我们报告了在合成数据集上进行实验的查询时间、构建时间和索引大小。具体来说，报告的查询时间是每个方法的总体运行时间，DFS、聚焦DFS、war应力、采样树和选择树，以处理总共10,000个随机LCR查询，以毫秒（毫秒）为单位，而构建时间以秒（秒）为单位。采样树的构造时间是构造近似最大生成树和NT的时间，而Warshall的构造时间是得到完全传递闭包的时间；指数大小以千字节（KB）为单位。对于Warshall，索引大小是广义传递闭包的大小；对于采样树，它是生成树的大小T+NT的大小。此外，采样大小是采样树（霍夫丁-伯恩斯坦树，算法2）的采样顶点的数量，“-”意味着该方法在图上不起作用（主要是由于内存成本）。
（Expr1.a）ER图上的变化密度：在本实验中，我们将|V | = 5000和范围密度|E| |V |从1.5固定到5，以研究索引大小、查询时间和索引构建时间如何随图密度而变化。表1(a)显示，由于权值误差很小，最多可以使用800个顶点有效地构造采样树，其性能以及精确的最优最大生成树。表1(b)显示，在Expr1.a中，当密度从1.5增加到3.0时，采样树的指数大小不仅很小，而且仅增加了1.5。沃尔的指数尺寸不仅大29到510倍，而且对密度更为敏感。虽然|E|/|V |从3.5到5的施工时间大约是|E|/|V | = 1.5的10倍，但War应在高密度下完全不能工作。此外，随着|E|/|V |的增加，采样树的查询时间几乎保持不变，如图10(a)所示，尽管DFS和Focused|V|的查询时间显著增加。这表明采样树可以处理相对密集的图。
（Expr1.b）ER图上不同的查询约束大小：在这个实验中，我们修复了||=5000，密度||||=1.5，然后将查询标签约束||从总边缘标签的15%修改到85%，以比较这些方法之间的不同。表1©显示，在Expr1.b中，war应指数大小约为采样树的400倍，而施工时间约为采样树的15倍。此外，当|A|增加时，DFS的查询时间是采样树的20到40倍，如图10(b).所示综上所述，本实验表明，采样树在增加查询约束大小时可以很好地表现良好。最后，我们注意到，聚焦DFS的性能甚至比没有可达性索引的DFS还要差。通过进一步的分析，我们发现，由于有向图的连通性相当良好，因此由于可达性指数而被修剪的搜索空间非常小。在这种情况下，在搜索过程中在每个顶点上查询传统的可达性索引不会产生回报，而只是成为聚焦DFS的额外成本。
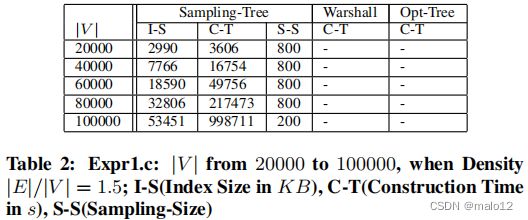
（Expr1.c）ER图上的可伸缩性：在这个实验中，我们固定了密度|E| |V | = 1.5，然后将图的大小|V |从20,000改变到100,000。由于可达性索引的内存成本，聚焦DFS不能处理非常大的图。此外，当顶点数量超过20,000时，Warshall和Opt-Tree也会由于内存瓶颈而失败（表2）。因此，我们只报告了采样树和DFS的实验结果。表2显示，构建最优生成树只需要少量的样本顶点（S-S）。图10©显示了DFS的查询时间是采样树的75到400倍。总之，当增加图的大小时，采样树的比例很好。
（Expr1。d）在SF图上改变查询约束大小：在这个实验中，我们修复了基于RMAT算法的|V | = 5000，然后将查询标签约束|A|从总边缘标签的15%改变到85%，以比较这些方法之间的区别。当增加|A|时，DFS的查询时间是采样树的35到40倍，聚焦DFS的查询时间甚至是采样树的151到261倍，如图10(d).所示Expr1。d表明，当增加SF图的查询约束大小时，采样树可以表现良好。
（Expr1.e）SF图上的可伸缩性：在本实验中，我们基于RMAT算法生成SF图，并将图的大小|V |从20,000变化到100,000。类似于Expr1.c，当顶点数量超过20,000时，聚焦DFS、Warshall和选择树在我们的机器上出现故障。DFS的查询时间是采样树的370到2365倍，如图10(e)所示。这表明，当增加SF图的大小时，采样树的比例很好。


综上所述，在我们的查询时间的实验结果中，采样树比DFS、聚焦DFS快得多，并且非常接近Warshall，后者具有预期的最快的查询时间。平均而言，采样树在Warshall查询时间的3倍以内，比DFS快20到400倍，甚至比聚焦DFS快2365倍。采样树的索引大小比Warshall的要小得多，范围为广义传递闭包的0.1%到0.3%。这些结果表明，采样树算法在有效地回答ER图和SF图的非常紧凑的索引性查询方面是非常成功的。

6.3 Results on Real Datasets

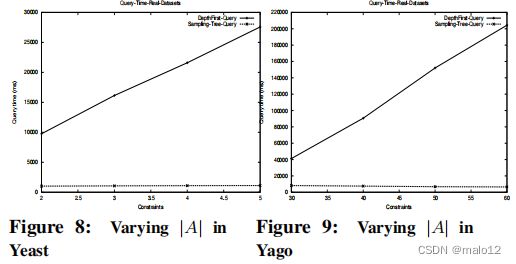
在这个实验中，我们在两个真实的图数据集上评估了不同的方法：第一个是酵母[18,13]的集成生物网络，第二个是来自语义知识网络，Yago [24]。酵母图包含3063个顶点（基因），密度为2.4。它有5个标签，对应于不同类型的相互作用，如蛋白质-dna和蛋白质相互作用。由于蛋白质之间的相互作用是无向的，我们将其转化为两个有向边。在实验研究中，我们使用采样树来构建索引，然后我们将标签约束|A|的大小从2变化到5来研究查询时间。与DFS相比，采样树在酵母图上平均快2倍。第二个Yago图包含5000个顶点有66个标签，密度为|E|/|V | = 5.7。由于标签的大小很大，所以我们不在采样树中执行采样。相反，我们只需计算单个源路径标签。我们仍然称它为采样树，因为这个过程可以看作是采样算法的一个特例。在这里，我们将标签约束|A|从20改变到60。图9显示了我们的索引方法在yago图上要快5到31倍。总之，我们可以看到，在真实的数据集中，我们的方法对于回答标签约束查询是有效和有效的。

7. CONCLUSION

本文引入了一个新的带有标签约束的可达性问题。这个问题在现实世界中有很多潜在的应用，从社会网络分析、病毒式营销到生物信息学和RDF图管理。一方面，这个问题比传统的不涉及任何标签约束的可达性查询更为复杂。另一方面，这个问题可以看作是在标记图上的简单正则表达式路径查询的特例。然而，我们的新问题可以在多项式时间内解决，而不是np困难的。在这项工作中，我们开发了一个新的基于树的框架来压缩广义传递闭包的标记图。本文提出了一种利用有向最大加权生成算法来优化指数大小的新方法。我们推导了一种基于几何搜索数据结构的快速查询处理算法。我们对真实数据集和合成数据集的实验评估表明，我们的方法可以平均将传递闭包压缩两个数量级以上，同时它可以提供非常接近完全物化传递闭包的查询处理。