【论文阅读】DLCR : Eficient Indexing for Label-Constrained Reachability Queries on Large Dynamic Graphs
Chen X, Peng Y, Wang S, et al. DLCR: efficient indexing for label-constrained reachability queries on large dynamic graphs[J]. Proceedings of the VLDB Endowment, 2022, 15(8): 1645-1657.
ABSTRACT
许多真实世界的图,如社会网络、生物网络、知识图,自然都有边缘标签,不同的标签表示节点之间的不同关系。在这样的边缘标记图上,一个重要的查询是标签约束可达性(LCR)查询,我们得到一个源s,一个目标t,一个标签集Ψ,目标是检查是否存在任何路径?从…向边缘的标签在吗?它们都属于Ψ。现有的LCR查询的索引方案仍然关注静态图,尽管许多边缘标记图本质上是动态的。
基于现有解决方案的局限性,我们研究了如何在动态图上有效地维护索引方案。我们提出的方法是基于最先进的LCR查询的2跳索引。在本文中,我们提出了为响应动态边缘插入/删除而更新索引结构的有效算法,并证明了我们的更新算法的正确性。随后,我们提出,采用一种查询友好但更新不友好的索引方案,可以产生令人惊讶的卓越的查询/更新效率,并优于那些更新友好的索引方案。我们分析并证明了查询友好的索引方案实际上达到了与更新友好的方案相同的时间复杂度。最后,我们提出了批更新算法,其中更新可能包括多个边缘插入/删除。大量的实验表明,所提出的更新算法、查询友好索引方案和批更新算法的有效性。
1 INTRODUCTION
图是一种捕获实体之间复杂连接的基本数据结构。许多真实世界的图表,例如,社交网络、生物网络和知识图都是边缘标记的,其中每条边都与一个标签相关联,不同的标签表示不同的关系。例如,在社交网络上,两个用户之间的关系可以采取多种形式,例如,“关注”、“喜欢”和“朋友”。在这样的边缘标记的图上,图查询的一种基本类型是标签约束的可达性(LCR)查询。在LCR查询中,它将源节点?、目标节点?和标签集Ψ作为输入。如果存在一条路径,则该查询将返回true?从…向这样的标签吗?每条边缘吗?在路径上有什么问题吗?属于Ψ,否则返回false。如[13,20-22,28]所示,LCR查询了在社交网络、生物网络、知识图等方面的许多应用。例如,在一个社交网络上,一个LCR查询可以用来确定两个顶点是否通过一系列给定的关系相关联。应用程序的另一个例子是关于知识图的。常规路径查询已经在知识图[3,4,31]上进行了广泛的研究,并被实用的图查询语言所支持,如SPARQL 1.1、PGQL [27]和openCypher[11]。LCR查询是常规路径查询中最重要的运算符之一。
在上述应用程序中,图通常是动态变化的。例如,在社交网络上,两个节点可能会产生新的连接或互动。在知识图上,在知识获取过程中可以识别两个节点之间新的关系。然而,Peng等人提出的最先进的索引方案P2H+ [21]是基于2跳索引的,并假设输入图是静态的。当图表发生改变时,P2H+索引就不再工作了。在每次更新后从头开始计算P2H+索引并不是一个合理的选择,因为索引的构建仍然需要相当高的预计算成本。另一种解决方案是进行图遍历,例如,BFS/DFS,并验证是否存在任何满足标签约束的路径。然而,在现实应用程序中的标记图往往是巨大的,这使得使用在线图遍历回答LCR查询代价昂贵。为了避免昂贵的在线遍历,到达[28]是一种无索引的、基于采样的算法,适用于大型动态图。然而,到达只能提供一个近似的结果,并且只有在输入图是强连接的时才提供理论保证,而许多标记图通常包含层次结构,而不是强连接的。此外,查询到达时间比P2H+慢近1000倍。这些限制了近似到达的应用。
主要贡献。由于现有解决方案的局限性,我们研究了如何在动态图上设计一个既灵活且可扩展的索引方案,同时提供精确的查询结果。我们的解决方案是基于最先进的P2H+2跳索引[21]。不是从头计算索影响的节点,而是预先计算然后更新一组受影响的节点只对这些由边缘插入/删除引起的受感染节点的索引结构进行处理。虽然对特定节点进行更新的想法并不新鲜,但细节却在于魔鬼。目前还不清楚如何有效地识别这些受感染的淋巴结。给定一个边插入
此外,图形更新可能会分批进行。我们进一步设计了批处理更新算法,以便当集体更新可以受益时,我们的批处理更新算法提高了实际效率。我们将展示如何设计插入和删除的批处理更新算法,并讨论改进的效率背后的基本原理。对于我们的批量插入(回复。删除)算法,它最多可以达到一个算法。插入速度的数量级。一个接一个地处理更新的算法。
最后,由于图是动态变化的,维护索引结构的一个自然想法是采用RB-tree等更新的数据结构。然而,我们证明了令人惊讶的是,查询和更新操作都受益于维护查询友好但更新不友好的数据结构,例如,通过一个排序的动态大数组。为了解释,即使在更新中,也需要执行frst查询,查询效率成为主要的瓶颈;因此,使更新效率的关键是查询效率。这一发现也可能为如何设计有效的动态指数结构提供见解还有用于其他查询的2跳索引方案。理论分析表明,具有查询友好设计的插入/删除/查询算法与具有更新友好数据结构的算法具有相同的时间复杂度。
综上所述,我们的主要贡献如下。
动态LCR指数(DLCR)。据我们所知,这是在大图上快速研究LCR问题的全动态算法的首要工作。我们设计了更新算法,使其只需要更新一小部分受影响的节点,使其具有超优越性。
批更新。此外,还提出了批量插入和删除技术,以进一步提高性能。
友好的设计。我们进一步研究了如何在考虑底层数据结构的选择时使更新更加方便。我们证明了一个查询友好的设计实际上比一个更新友好的设计实现了显著的改进。
活力和活力。我们的实验表明,我们的算法与基线相比的有效性和有效性。
2 PRELIMINARY
本节介绍了问题的识别,然后讨论了最先进的索引方法。表1总结了本文中使用的关键符号。
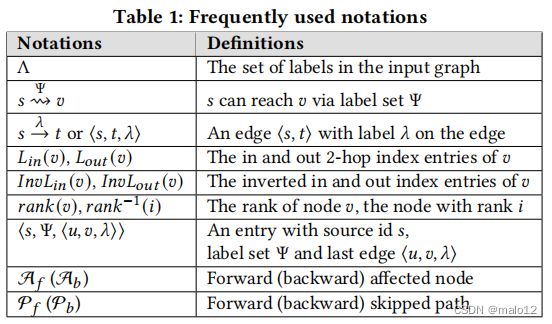
2.1 Problem Definition
输入图G= (V,E,Λ)是一个有边标签的有向图,V是n个节点的集合,Λ是一个非空标签集,E⊆VVΛ是一个有向标记边。例如,e=
定义1(标签限制的康复功能)。给定源节点、目标节点和标签集Ψ,如果存在Ψ路径,则标签约束可达性(LCR)查询返回true?向否则将返回false。
另外,我们说一个标签集Ψ⊆Λ是一个最小的标签集连接吗?向如果(i)?Ψ{ ?和(ii)吗?Ψ ′ ✚✚{?对于任何标签集,Ψ‘⫋Ψ。
2.2 2-Hop Cover Framework
2跳覆盖技术已经在文献中得到了广泛的研究(如[1,2,6,7,29,30,33])。我们的方法遵循相同的框架。在LCR查询的2跳索引中,有两组索引条目Lin和Lout,表示为顶点的入口集和输出集in-entry,out-entry分别为每个顶点v。对于入口集Linv,它以的形式存储一组元组?,Ψ???,它对应于一个Ψ?-路径?从…向和最后一条边连接到了吗?在路径上有问题吗?。用于外入口集lout(?),它以相同的形式存储了一组元组。假设有条目?Ψ???是在????中出现的吗(?),然后它表示一个Ψ?-路径从?向而它的起始边缘是什么?从…是我们使用一个占位符·,例如,?,Ψ?,·⟩,如果元组中相应的信息在上下文中不匹配。另外,我们使用什么?Ψ⇝ ?来表示与一个条目对应的路径。

给定这样的属性,要回答一个LCR查询与输入源节点s,目标节点t,和标签集Ψ,它可以简单地返回真,如果一个节点?都存在于两个Lout(s),Lin(t)中(?)和(?)到这样的程度Ψ-覆盖物吗?向否则将返回false。
我们说,如果删除任何条目将导致某些查询的LCR查询答案错误,即,一些查询在删除后不会被条目覆盖,则至少是2跳覆盖。请注意,不一定所有的2跳索引都是最小的,因为我们可以简单地添加更多的条目,而不影响查询的正确性。首先,我们将详细说明标签约束的BFS,然后是Peng等人[21]提出的LCR查询的最先进的2跳索引方案prun2-Hop(简称P2H+)。
2.3 Existing solutions for LCR Queries
LC-BFS.我们解释了标签约束宽度频率搜索(LC-BFS)如何工作,因为最先进的P2H+指数是通过LC-BFS与修剪策略的迭代方式构建的。给定一个来源吗?,LC-BFS的工作原理如下。它不是维护一个队列,而是维护|Λ| + 1队列Q0、Q1、Q1、Q2、···、Q|Λ|来跟踪路径从?要访问的节点及其对应的标签集,队列在哪里??记录通过大小为?的标签集访问的节点。就像BFS如何跟踪路径一样,我们也会维护路径的最后一条边来对路径进行编码信息。对于每个节点?,它不是维护一个访问标记(就像对典型的BFS可以做的那样),而是维护一个集合S?对Ψ,??表示对于任何标签集Ψ∈S,,s可以使用Ψ-reach吗?通过最后一条边的ev。开始为每个节点设置为空??。下一个,?,∅,????添加到?0中,其他队列初始化为空。在BFS遍历期间,在每次迭代中,它总是将标签集大小最小的队列取消队列。假设它的路径是这样的吗?已从队列??,中退出队列然后它表示?0到????−1为空。进一步假设退出排队的路径?是否在节点处结束?与一个标签集Ψ?.。然后,在这个迭代中,它检查是否存在任何条目Ψ,·∈S?这样的Ψ吗?⊆ Ψ.如果是这样,有的话,路径呢?被修剪和迭代的鱼鳍。否则,一个条目Ψ,·被添加到??frst.接下来,它检查了每一个外向的优势??= (?,?, ?)的并将标签设置为Ψ?= Ψ?∪ {?}.为路径吗?′正在经历吗?和边缘??,然后将它添加到队列中?|Ψ?|和迭代的鱼。当所有队列都为空时,LC-BFS将终止。
上述算法可以用于用?作为源节点(目标节点的选择和标签集的选择)。如果目标节点和标签集Ψ也被给出,算法一旦我们找到一个路径就终止?它可以连接起来吗?向通过一个标签集Ψ‘⊆Ψ。
LC-BFS的时间复杂度可以由?(2 |Λ| · (n+m)).要解释,对于每个节点?,有吗?(2 |Λ|)在最坏情况下彼此不是彼此子集的不同标签集。因此,我们最多2 |Λ|次探索每个节点和每个边。

例子1。考虑一个输入图G1,如图1(a).所示标签的集合Λ是{a,b}和|Λ| = 2。因此,我们维护了3个队列:Q0、Q1和Q2。假设我们从节点1开始进行LC-BFS。最初,对于每个节点?,我们维护一个集合Sv初始化为空集,将1、∅、·添加到?0中,并将?1初始化到?2设置为空。
在第一次迭代中,1、∅、·从Q0中退出队列。由于Q1为空,∅,·被添加到Q1。接下来,跟随节点1的输出边1,3,a,我们通过标签集{?}获得从1到3的路径?1并将?1添加到?1中。在下一次迭代中,路径?1从?1退出队列,因为?1是具有最小iD的非空队列。因为?3是空的,,·⟩已被添加到?3中。然后访问边缘34和34。从节点1到4通过标签集{?}和路径?3从节点1到4通过标签集{?,?}都是派生出来的。然后,我们将2加到1,将3加到2。
接下来,通过标签集{?},从节点1到节点4的路径?2已从?1中退出队列。因为?4是空的,所以有一个条目{?},·⟩已被添加到?4中。由于节点4没有外邻居,所以迭代就会消失。之后,通过标签集{??}从节点1到4的路径3?已从?02退出队列,因为?0和?2为空。作为?4,包括一个条目,·⟩是这样的,所以{?}⊆ {?, ?},路径3被修剪,当前迭代消失。在此迭代之后,所有队列都为空,并且节点1中的LC-BFS终止。
P2H+指数。P2H+指数是根据顶点等级建立的2跳指数,其防御能力如下。
定义2(顶点等级)。假设顶点id已经被映射到1到?在哪里是图中的节点数。让是来自{、2的双射到{1、2、。。那么节点的顶点秩呢?是(?).
有很多方法可以消除顶点的秩。在P2H+指数中,节点按其程度进行排序。特别是,rank(v)的一个节点吗?被定义为按度的递减顺序排序的节点的秩(其中关系是任意打破的)。那么,度最大的节点w1将具有rank(w1)= 1,而节点wn与最小的度有rank(wn)=n的值越小(?)的一个节点吗?是,排名更高的节点吗?有我们进一步削弱了rank−1 (i)作为具有i-th排名的节点。请注意,如果节点的秩是固定的,则P2H+索引是唯一的。
给定顶点秩,然后以迭代的方式构造P2H+索引。特别是,在第i次迭代中,两个lc-bfs从wi= rank−1 (i),即排名第i的节点。特别是,一个向前的方向。LC-BFS在图上按照方向进行处理。相反的方向)的边缘。我们使用rank(?)和(?)指示在第?次迭代中构建的索引。首先,我们添加了一个索引
定义3(已跳过的路径)。有一个路径吗?从…向在LC-BFS期间,如果它被当前的P2H+指数所覆盖,则它是一个被跳过的路径。
当维护的队列为空时,修剪的LC-BFS结束。接下来,处理后向的LC-BFS,并处理输出项Lout都是构建起来的。最后,我们要分配了Lini+1 (v)←Lin (v)和Lout+1(v)←Lout (v)对于每一个人吗?∈ ?然后转到(i+1)次迭代。指数建设什么时候都完成了n节点影响了前向和后向的LC-BFSs。
P2H+索引构造算法的时间复杂度是什么?(2 2|Λ| ·?2 · (?+?))如在[21]中所分析的那样。为了解释,在修剪过的LC-BFSs期间,它需要检查它是否会被每个访问路径的现有P2H+指数所覆盖。这将导致On·2 |Λ|)在最坏的情况下的成本,因为一个节点的进入和退出最多包括?(?·2 |Λ|)项目。既然向前和向后修剪LC-BFSs访问?(2 |Λ| · (?+ ?))路径和它需要进行吗?(?)乘以,总成本可以以?(2 2|Λ| · ?2 · (?+ ?)).
例子2。仍然要考虑如图1(a).所示的输入图假设这样吗?rank(i)= i.首先,我们先添加1,∅,null至“是否正确?”lout(1)和lin(1).然后,我们从节点1进行LC-BFS,因为LC-BFS排名最高。节点1的初始设置与示例1中的初始设置相同,除了我们没有维护Sv。
最初,对于节点1的输出边1、3,导出路径1并将其添加到队列1。然后,在frst迭代中,路径P1从Q1退出队列,它通过{a}检查1到3可以被覆盖吗?Lout(1)和Lin (3).因为答案是否定的,所以有一个条目1,{a},·⟩被添加到了吗Lin (3).然后,沿着节点3的输出边缘,通过标签从节点1到节点3设置{a,b}和?3从1到3通过标签设置{a,b}被派生并分别添加到Q1和Q2中。接下来,路径2退出队列,1,·⟩被添加到了吗Lin(4).那么,路径3退出排队,可以由Lout(1)和Lout(4)因此就被修剪掉了。正向LC-BFS结束。
接下来,从节点1开始进行向后的LC-BFS。首先,通过标签集{a},从节点1到节点6的路径?4在反向图上推导并添加到队列?1。在第一次迭代中,路径P4将退出队列。因为P4的反向路径不能被Lout6所覆盖吗?Lout(6)和Lin(1),一个条目1,·⟩被添加到了吗?Lout (6).然后,导出反向图上从节点1到节点5的路径?5并添加到?1中。在下一次迭代中,路径数?5将退出队列。因为?5的反向路径不能被覆盖吗?Lout(1)和P(5),一个条目1,·⟩被添加到了吗?Lin(5).由于节点5没有进入的边缘,向后的LC-BFS鳍鱼。这个1 a(·)和吗?1 a(·)然后被复制为Lout(·)和分别为(·)。指数和指数指数如表2所示。
备注。由于对空间的兴趣,对于我们在表2-4中显示的索引,我们省略了条目?,∅,·从每个节点的入口和输出?;我们用一个字符串吗??表示该集合。我们提出的DLCR是基于最先进的P2H+指数。接下来,我们将详细说明动态图的DLCR。
3 DLCR INDEX FOR DYNAMIC GRAPHS
给定一个输入图G,假设在一组更新操作之后,该图变成了G′ .这里我们只考虑边缘的插入/删除,因为节点的插入/删除可以很容易地映射到一组边缘的插入/删除。我们的主要想法是提供一个轻加权的方案来充分利用该指数为?并及时更新索引,使更新后的索引与P2H+为for?′从零开始。我们称这个属性更新为不变量。我们的DLCR是更新不变的,它表明我们的DLCR索引在每次更新后是唯一的,因为相同的顶点顺序。我们的DLCR索引调整如下:
定义4(DLCR)。给定一个rank(v)每个顶点的值吗?,DLCR索引是根据修剪后的LC-BFS构造的最小2跳索引。给定一个边的更新,将更新后的图表示为:G′,更新后的索引满足更新不变性,即,索引与从头重新构建使用修剪后的LC-BFS按照每个顶点的秩顺序在G′ 。
我们的DLCR索引也是更新友好的,我们将很快显示。我们的DLCR不是从零开始重新构建,而是仔细地派生出一小组受影响的节点,然后只对那些受影响的节点更新索引。我们将在第3.1节中详细介绍我们的插入算法和第3.2节中的删除算法。
3.1 Insertion Algorithm
在本节中,我们将详细介绍插入算法的细节。在引入插入算法之前,我们建立了一个辅助数据结构来支持有效的索引更新。
定义5(倒置的2跳索引)。通过倒置原始的2跳索引,可以创建一个反向的2跳索引。给定一个索引entry
表2显示了一个反向索引的一个例子。接下来,我们将详细阐述插入算法的主要思想。

主要想法。插入新的边,现有路径和添加的边将生成新路径,而这些路径可能不会被目前的2跳指数所覆盖。例如,假设我们在图1(b)中添加了一条边4,5、?,那么节点1就可以通过标签集{?}到达节点5在添加此边之后。但是,现有的2跳索引并不包含这条路径。所以我们需要生成新的索引条目来保持2跳的覆盖属性,这就是说,如果?可以到达吗?通过标签集Ψ,那么我们总是可以找到一个节点吗?这样存在一个条目v,Ψin,·⟩在入口集Lin(t)中的和一个entry在入口集????(?)的节点吗?这样的Ψ??⊆Ψ和Ψ???⊆ Ψ.对于上述从节点1到节点5的新路径,我们需要添加一个在条目1,{?},4,5,?进入???(5),它可以从现有的条目1,{?}中生成,·⟩在???中(4)加上的边45?。我们将很快详细说明如何寻找这样的新道路。高级的思想是将修剪后的LC-BFSs应用于fnd,并添加这些新条目,以满足索引条目的2跳覆盖特性。
在添加这些新条目以使索引满足2跳覆盖属性后,一些旧的条目可能会变得冗余,即删除它们不会违反2跳覆盖属性。我们的目标是保持索引的最小属性,因此应该删除这些冗余的索引。表3说明了添加条目以满足2跳覆盖属性后的索引条目。进入的5,·⟩在???中(6)是多余的,因为它是2跳覆盖的1,{?},·⟩在????中(5)和1,{?},·⟩在???中 (6).因此,可以在不违反2跳覆盖属性的情况下删除该条目。根据以上观察,我们的插入算法包括两个步骤:
添加条目。这个阶段添加了新的条目,并将受缺陷的节点(在缺陷6中)定位在正向和反向方向。
删除冗余。它将删除受到影响的节点上的冗余条目。接下来,我们将解释我们设计这两个步骤背后的基本原理。
基本原理和算法细节。我们首先考虑需要添加到DLCR中的索引条目的属性(否则它将违反2跳覆盖属性)。对于这些条目,我们有以下引理。
引理1。对于所有需要添加到DLCR的条目,它至少覆盖了一个穿过插入的边的新路径。
所有被遗漏的证明都可以在我们的完整版的技术报告2中找到。基于引理1,我们有了关于索引项的定理1,这些索引项需要添加,以保持2跳覆盖属性。
定理1。对于每一个入口(回复。需要添加到DLCR以维护2跳覆盖属性,它对应于一个正向的访问路径(例如。从一个源节点上修剪过的LC-BFS吗?在Lin(u)(Lout(v)).
给定定理1,可以添加维护2跳覆盖属性的新条目如下,其中算法1显示了添加项阶段的伪代码。首先,让我们吗?是???中的节点集(?)和(?)(算法1,第2行)。然后,按照?中节点的排名,一个前进。LC-BFS与节点一起进行?作为资料来源,如果是什么?出现在???中(?)(代表.????(?)).算法1行4-8显示了从节点?正向修剪LC-BFS的伪代码。而不是从头开始进行LCBFS?,它只从将通过新插入的边缘的路径开始????。因此,对于每个索引条目?,Ψ,·,我们添加一个条目?,Ψ∪{?},·⟩到?|Ψ∪{?}|(算法1行4-7)。然后,对初始化的队列?0、···、?|Λ|进行修剪后的LC-BFS。在修剪的LC-BFS期间,在每次迭代中,它删除路径?从…到一个节点吗?通过标签设置Ψ?具有大小最小的标签集。如果是路径吗?可以被当前的2跳索引覆盖,然后路径被修剪。否则,路径会吗?没有修剪,然后进入?,Ψ?,·插入到???(?).类似地,一个向后的LC-BFS是进行的,如果?出现在????中(?)(算法1,第9行)。根据定理1,在添加这些索引项后,满足了2跳覆盖特性。

然而,在创建新的条目后可能存在冗余的条目,即删除这些条目不会违反2跳覆盖属性。关键的挑战是如何有效地定位这些冗余的条目。我们首先转移了有缺陷的节点。
定义6(受影响的节点)。一组受影响的节点的A是:一个= {?| ???(?)???(?)已了。如果(?)(代表.????(?))已更改,节点?被称为前锋。向后)在A?(回复。在A中的一个?)。受影响的节点有助于定位冗余条目。
定理2。对于一个前进的方向。受缺陷的节点?∈ A?(回复。A?),如果它包含冗余条目,则它们必须存在于???中(?)或(?)(代表.????(?)或(?)).
根据定理2,我们可以通过检查缺陷节点的条和倒条来删除冗余标签。这里我们讨论前向感染节点的情况,而情况对于反向感染的节点,也可以类似地处理。算法2显示了伪代码。特别是,对于一个正向受到缺陷的节点??,它会试图删除每个条目吗?=⟨吗?,Ψ,·在???中(??)看看LCR的查询是否来自??向通过标签集,Ψ可以被2跳索引覆盖而不使用吗?(通过调用??????????????)。我们省略了??????????????的伪代码因为它很简单。如果答案是肯定的,那么输入吗?是冗余的,并且可以安全地从???中删除吗(??)并从??????中去除相应的反向指数(?)(算法2,第1-4行)。接下来,它会检查每个条目?′ = ⟨?‘,Ψ’,·,在???????中(??)并检查是否删除相应的索引??,Ψ′,·在????中(?′)仍然可以覆盖的LCR查询从?“到”??”通过标签集Ψ‘。如果答案是肯定的,则条目为??,Ψ′,·在????中(?′)是冗余的,并已从????中删除(?′)和吗?‘也被从???????中删除(?′)(算法2行5-7)。接下来,向后受感染的节点也用???????????????进行处理算法伪代码以镜像方式处理。

算法3给出了插入算法的细节。假设附加的边是

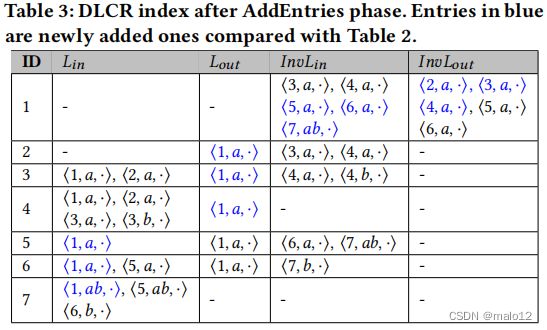
例3.假设<4,5,a>被插入G1中,如图1b所示。原始索引是Table2。开始,我们用Lin(4){<1,{a},·>,<2,{a},·>,❤️,{a},·>,❤️,{b},·>}和Lout(5){<1,{a},·>}创造新的入口。我们从高级级到低级开始。在第一次迭代中,我们从节点1开始,它对应的进入口和出入口为<1,{a},·>和<1,{a},·>。对于正向版本,在应用修剪后的LC-BFS后,我们把<1,{a},·>添加到Lin5,<1,{a},·>添加到Lin6,<1,{ab},·>添加到Lin7。后向版本,我们添加<1,{a},·>到Lout4,<1,{a},·>添加到Lout3,<1,{a},·>添加到Lout2。在第二次迭代,我们从节点2,只有一个进入<2,{a},·>。运用剪枝LC-BFS,这些entry也被存在的entry剪枝。这个迭代终止和添加项阶段。前向感染节点为5、6、7,后向感染节点为2、3、4。表3显示了添加项阶段之后的条目。然后转到删除冗余阶段。以反向感知节点6为例。我们首先在Lin6中确认entry。标签<1,{a},·>不是冗余的,因为QuerySkipEntry(1,6,{a})
返回false。第二,我们检查Lout6的entry。因为InvLout6是空的,我们停止。Table4汇总了最终的DLCR索引。
我们的插入算法的一个优点是,更新后的索引是唯一的,并且与从头开始构建的索相同?′由P2H+指数计算。接下来,我们证明了DLCR是更新不变的,并分析了我们的插入算法的时间复杂度。

正确性和复杂性分析。接下来我们证明DLCR索引是更新不变的。给定一个边插入,让附加项阶段之后的索引是?′和删除冗余阶段后的指数是什么?∗ .让是由P2H+从零开始建立的指数。我们有索引的引理2?′在附加程序阶段之后,
引理2。对于每个节点?,?′ ??(?)(回复。吗?′ ???(?))是???的一个超集吗(?)(代表.????(?)),i.e., ???(?)⊆ ?′ ??(?)(代表????(?)⊆ ?′ ???(?)).
我们有关于一个条目的冗余性的引理3。
引理3。对于???中的每个条目(?)(代表.????(?)),它不是在?′ ??(?)(回复。吗?′ ???(?)).结合引理2和3,我们有以下定理。
定理3。插入DLCR的算法后,索引吗?∗和索引完全一样吗?由P2H+指数从零开始构建。定理3表明,DLCR在边插入后是更新不变的。我们现在考虑算法3的时间复杂度。在frst步骤中,我们从???中修剪了LC-BFS(?)和(?).让是在???中出现的节点集(?)和(?).然后是??????????的时间复杂度阶段是什么吗?(2 2|Λ| · |?| · ?· (?+ ?)).让是添加的输入项或输出项的集合。然后,最多有|????|感染的节点。对于每个被感染的节点,它会检查吗?(2 |Λ| ·?)对于每个条目,它需要一个查询并运行?(2 |Λ| · ?)代价因此,?????????????阶段需要吗?(|????|2 |2Λ| ·?2)成本。把它们加在一起,时间的复杂性是什么? 2 |2Λ| · ?· (|???| · ?+ |?| · (n+m)) .
3.2 Deletion Algorithm
主要想法。在删除边时,一些路径可能会消失,因此当前索引可能会返回不正确的查询答案。我们称这样种索引条目为过时的条目。例如,假设我们删除了图1(b)中的?2中的边4、5、?,因此图变成了?1,如图1,(a).所示然后,进入1,4,5,?英寸???(5)自路径1 {?}由于删除边缘4,5,⇝5不存在。在删除过时的条目之后,需要重新激活一些被跳过的路径,它们在删除之前会被过时的条目修剪,以创建新的条目。例如,2、3、{?},2、3、?是一个被跳过的路径,需要重新激活。为了解释,在???中现有的入口2,∅,·(2)可以通过边缘2,3,?,并生成新的入口2,{?},2、3、?,删除后不需要修剪,应该插入到???中(3)(见表4)。需要重新激活这些被跳过的路径以添加新的条目。总之,该删除算法包括三个步骤:
删除条目。它将删除过时的条目和找到所指定的节点。
位置跳过路径。它会定位要重新激活的跳过路径。
创建新条目。它通过修剪的LC-BFSs使用第二阶段找到的有效跳过路径创建新的条目。
基本原理和算法细节。接下来,我们将解释这三个步骤是如何逐个工作的。在第一步骤中,为了查找过时的条目,我们有以下引理。
引理4。所有过时的条目都通过被删除的边缘??。
给定删除的边??,?,引理4表明所有过时的条目都经过这个删除的边。我们注意到,对于一个给定的索引项,它对应于一个路径?从…向在哪里有最高的排名吗?,每个子路径?从哪里开始吗?也对应于一个索引条目。情况在什么时候?排名最高的将有镜壳。若要使用此属性,每个条目都将存储一个????????属性,它是通过修剪的LC-BFS在索引构建过程中插入相应条目之前的最后一条边。有了这个属性,我们现在能够有效地定位经过被删除边缘的索引项?= ⟨?, ?, ?⟩.特别地,我们首先检查了???中的索引条目(?)并找出其????????的条目是然后,我们从???开始(?)以及更多的过时条目?。

算法4详细说明了如何根据???中的条目来查找过时的条目(?)谁的被删除的边是什么????。特别是,它可以在???中的条目(?)谁的是??????并将它们添加到设置A?。(算法4,第2-3行)。接下来,对于每个这样的条目?,Ψ,·,它frst从???删除条目(?)(算法4,第5行)。然后,它从?只不过是,它用路径初始化队列?从…向通过标签设置Ψ(这样它就不需要从源代码中执行BFS了?如算法4第6行所示;(ii)在BFS遍历期间,如果一个路径是否有终点?它的排名高于?,即,????(?)< ???(?),那么,路径可以被修剪,因为我们正在检查路径与?作为最高的等级(算法4第10-11行);(iii)只探索输出边????1,使对应的索引条目为路径?′ = ?Ψ⇝ ??1 → ?存在于???中(?)(算法4,第13-16行)。为了走这样的道路吗?‘,它将路径添加到队列中,并删除对应于?‘在???中(?).如果索引项在???中不存在(?),然后,在该路径上的遍历可以因为扩展的路径而终止从…索引条目中也不存在′。类似地,我们可以为????中的条目进行镜像阶段(?).而不是在做BFS上?′,它沿着图的相反方向向后进行一个BFS?′ .为了对空间的兴趣,我们省略了这个阶段的伪代码,称为bwddelentry阶段。
在删除过时的条目之后,我们需要查找由过时的条目修剪的跳过路径。在这种情况下,我们需要响应这些被跳过的路径,并在必要时为这些路径创建新的条目。这是第二步,即,locateskippedpath步骤,是我们的删除算法。这一步的主要挑战之一是如何有效地处理被过时条目修剪的跳过路径。为了实现这一点,我们记录了被ffe的节点,其中在frst步骤中包含过时的条目,并使用被ffe的节点创建被过时条目修剪过的跳过路径。
定理4。如果有一个路径吗?一个被跳过的路径是否被一个向前感知的节点所修剪?∈ A?并且在删除过时的条目后不被索引覆盖,那么(i)存在一个进入的边缘???和一个进入?,Ψ,·∈???(?)一起映射到这条路径上?,也就是说吗?Ψ⇝ ??→ ?到底是什么吗?;或(ii)存在一个条目?,Ψ,·在???????中(?)一个即将到来的边缘??这样??→ ?Ψ⇝ ?对应于路径?.。该情况是反向感染节点的镜像。
定理4表明,我们可以使用前向法。向后)受感染的节点到fnd跳过的路径。算法5显示了由给定的前向感知节点跳过的路径的伪代码。特别是,对于一个向前影响的节点?,它frst检查它的每个传入边,看看是否存在由于?引起的跳过路径。特别地,让?,?,??是?的输入边缘,然后它通过每个条目?,Ψ,·在???(?)看看LCR的查询是否与?作为资料来源,是吗?作为目标通过标签集Ψ∪{?}可以由当前的索引条目所覆盖。如果答案是肯定的,那么答案是路径吗?= ?Ψ⇝ ??→ ?已经被覆盖过了。否则,路径吗?没有被覆盖,我们将该路径添加到被跳过的路径中(算法5行1-5)。然后,它转向第二种情况,即路径可能被向前受影响的节点修剪。特别是,它检查了???????中的每个条目(?).对于每个条目吗?,Ψ,·在???????中(?),它检查的边缘,看看路径??→ ?Ψ⇝ ?可能由现有的索引条目所覆盖。如果答案是是的,则可以丢弃该路径。否则,该路径将被添加到被跳过的路径中(算法5行6-10)。这就考虑了正向受感染节点的情况。同样地,我们可以由于向后感染的节点来寻找被跳过的路径。由于它们是算法5的镜像情况,所以我们省略了讨论。

在确定了被跳过的路径后,我们使用这些被跳过的路径在算法6中生成新的条目。与算法1类似,我们从具有高排名节点的跳过路径开始生成新的条目。特别是,对于被发现的跳过路径,我们将它们分成两组P?和P吗?如算法5所示。设置P吗?存储起始节点在设置P?存储其中结束节点具有最高排名的路径集。对于路径的两个终结点都没有最高排名的情况,那么这样的路径将不可能成为索引条目,否则它将已经被排名更高的节点覆盖。在把这些路径划分成P之后?和P?”吗?。然后,我们可以从排名最高的节点上依次进行正向LC-BFS和反向LC-BFS。让是在被跳过的路径(起始节点或结束节点)中排名最高的节点集,如算法6行1所示。然后,对于?中排名递减的节点,它在迭代中修剪LC-BFS。在第?次迭代中,让排名最高的节点为第??次。然后,它检索P?这样,被跳过的路径的起始节点就为“?”。然后,对于每个这样的路径??Ψ,·,它添加?Ψ?到队列?|Ψ|。然后,利用初始化的队列(算法1行3-7)进行修剪后的LC-BFS。接下来,它检索所有终点为的路径?在并处理一个向后的LC-BFS上?′和迭代的鱼。当所有的节点都在里面了吗?处理,新条目,算法终止。

算法7显示了DLCR的删除算法的伪代码。这个伪代码是不言自明的。第1-2行显示了deleteentries步骤第3-6行显示了locateskippedpath的步骤。第7行显示了createnewentries的伪代码步骤由于对空间的兴趣,我们的删除算法的一个例子被省略了,可以在我们的技术报告中找到。
正确性和复杂性分析。最后,我们证明了DLCR删除算法仍然是更新不变的。让′是在deleteentries之后的索引步骤和?∗是排在这三个因素之后的索引步骤让是由P2H+指数从零开始建立的指数。首先,我们有以下引理?在deleteentries后的′步骤。
引理5。在deleteentries之后DLCR删除算法的步骤,对于每个节点?,?′ ??(?)⊆ ???(?)和′ ???(?)⊆ ???(?).接下来,我们有以下定理?∗,在我们的DLCR删除算法后的索引。
定理5(更新不变性)。该指数吗?删除DLCR算法后的∗与?完全相同?由P2H+从零开始建造。
定理5表明,DLCR的删除也是更新不变的。接下来,我们分析了DLCR删除算法的时间复杂度。让是在???中出现的节点集(?)和(?).然后,它在?????????????中进行修剪过的BFS(注意,这里是BFS,而不是LC-BFS)从这样的节点走一步,谁的成本是?(|吗?|·(|Λ| +日志吗?)(?+ ?)).然后,在第二步中,对于每个被受感染的节点,它连接了边和它的内条目,其成本可以由?(?· 2 |Λ| ).因此,第二步的成本是什么?(|?| · ?· 2 |Λ| ).假设这个集合吗?包括在每个被跳过的路径中具有最高排名的节点的节点集。然后,第三步gennewentries它的成本是什么吗? 2 2|Λ| · |?| · ?· (?+ ?),,它主导了第二步的成本。其财务成本是什么?|吗?|·(|Λ| +日志吗?)+ |?| · 2 2|Λ| · ? (?+ ?) .备注。值得注意的是,更新后的索引不必相同。然而,更新不变量是一种优雅的状态,因为它是不变的,并且如果满足该属性,也可以方便地验证更新后的索引的正确性。
4 OPTIMIZATIONS
4.1 Query-Friendly Design
由于输入图是动态变化的,因此索引是动态变化的,因此自然会采用更新友好的索引设计。实际上,我们对索引结构的数据结构的最初选择是维护一个平衡的二叉搜索树,例如rb树,这样它就可以在索引查询和索引更新之间获得良好的交易。但是,如果我们仔细分析插入、删除甚至索引构造算法,我们可以观察到,使用DLCR索引进行查询是经常被调用的主要子例程之一。特别是,在插入过程中,给定一条插入边??,算法需要向前做。从???中的节点中修剪LC-BFS(?)和(?)在插项中阶段。在修剪的LC-BFS期间,它需要做一个查询来检查路径是否可以修剪。在删除冗余阶段,它再次需要频繁查询,以检查索引条目是否冗余。在删除算法中,它需要使用对现有索引条目的查询来定位被跳过的路径。在索引构建过程中,为了检查是否可以修剪路径,我们需要使用当前的索引进行查询。我们选择查询友好型设计的主要原因是,在所有的索引构建、DLCR插入算法和DLCR删除算法中,查询通常比索引更新更频繁。因此,即使底层数据结构是查询友好的,而不是更新友好的,由于查询处理成本的降低而带来的好处仍然可以帮助提高整体性能。
为了使索引更便于查询,在设计索引结构时,我们选择了排序后的数组作为???的底层数据结构和与二值搜索树设计相比,如?????(?,?,Ψ),这样的设计可以用????的线性扫描来进行查询处理(?)源节点的数量吗?和(?)目标节点的数量?。与二进制搜索树的设计相比,这使得查询对缓存更加友好。虽然这使得更新成本变成了什么样子?(ℓ),其中,ℓ为索引的大小。在更新之前,它需要查询索引,以检查要添加的条目是否为冗余。因此,即使我们采用了查询友好的设计,总成本(查询+即更新)也可以以查询成本为界。因此,索引构建、DLCR插入算法和DLCR删除算法的时间复杂度不会随着查询友好的动态数组设计而改变。此外,在实际实现中,我们可以通过标记这些无效的条目,然后在删除条目时将它们全部删除,这样来延迟数组的更新。这进一步降低了索引更新的成本。
正如我们将在实验中展示的那样,这种查询友好的设计可以大大有助于查询效率的改进。随着查询效率的改进,它进一步大大降低了索引构建成本、插入成本和删除成本。我们相信,这一观察结果也揭示了在其他类型查询的2跳索引上的更新算法的设计。
备注。我们注意到,也可以采用哈希作为替代方法。然而,它并不会帮助降低搜索的复杂性。回想一下给定的一个输入源吗?,一个目标节点?,和一个标签集Ψ,DLCR的LCR查询算法需要找到一个中间节点?这样的节点吗?都存在于两个????中(?)和(?),和Ψ-覆盖物吗?向即使使用哈希,我们也不能找到节点吗?在前头这意味着,在最坏的情况下,每个节点都是吗?在(?)需要检查,看看是否(i)标签Ψ-覆盖?到?,和(ii)使用哈希来查找???中的标签(?)浏览所有相关的标签?检查是否存在Ψ覆盖的标签?向因此,基于哈希的解决方案的时间复杂度与我们的数组设计相同。此外,使用阵列设计,它比阵列设计产生更多的空间消耗和更糟糕的缓存位置,因为阵列设计只需要扫描????(?)和(?)来回答该查询。
4.2 Batch Updates
我们的DLCR的另一个优化是进行批量更新。通过批处理更新,如果集体更新可以受益,那么我们的批处理更新算法可以帮助进一步改进更新效率。我们只考虑插入或删除在相同的情况批量在更新与边缘插入和删除混合的情况下,可以通过批插入和批删除来处理它们。接下来,我们将展示我们的批处理更新算法。
批量插入。回想一下,在插入时,第一阶段添加了新的条目,而第二阶段删除了被感染节点的冗余条目。当处理多个边插入时,我们可以延迟删除冗余阶段,直到生成所有使用添加的边的新条目。原因是这些冗余条目不会影响其正确性,如果这些冗余条目对查询的影响可以忽略不计,那么我们可以在处理批处理中所有节点的附加项阶段时删除冗余条目。
为了确定冗余条目是否会对查询处理产生负面影响,我们提出了一种基于预探测的方法,以选择是逐步删除冗余条目,还是推迟在批处理中删除冗余条目。我们的预探测策略主要比较了批量插入的运行时间,在我们的例子中是300,与单边插入版本。我们检查是否批插入的性能,这延迟了deleteredundant阶段为所有节点,将降低性能相比,插入算法处理边缘插入一个。如果性能下降,那么集体插入将不会帮助降低DLCR插入成本。因此,我们对每条边逐个处理DLCR插入算法。否则,集体插入有助于降低运行成本,并且我们将充分利用批处理插入。
批处理删除。在DLCR删除算法中,记得它包括三个步骤,直接删除过时的条目,然后找到跳过路径,然后添加条目。如果我们逐个删除边,每次处理DLCR删除算法中的一条边,对于发现的跳过的路径,如果稍后删除跳过的路径上的现有边,它可能会变得无效。对于前面添加的条目,如果删除了路径上的一条边,它可能会无效。
基于此观察结果,我们的批处理删除算法frst为批处理中的每个节点删除过时的条目。那么,它就会被设置为P吗?前染节点和P?返回向后受感染的节点。请注意,错误的节点集也可能在不同的删除中重叠,这避免了fwdskippedpath中的重复任务ℎ步骤。然后,在跳过路径发现过程中,它避免了包含批中任何已删除边的跳过路径,并且剩余有效跳过路径的大小与单边删除相比,要小得多,使第二阶段定位跳过路径的速度快得多。最后,在createnewentries步骤中,它再次减少了计算量。为了解释,如果每次边删除后更新,则在createnewentries中生成条目由于随后的边缘删除,后续删除可能会被删除。我们的批删除将过时的条目删除过程从新的条目生成过程中分离出来,这样新的条目一旦添加到索引中就不会被删除。此外,在createnewentries步骤中,它将多个被跳过的路径与同一源结合在一起,可以帮助降低修剪后的LC-BFSs的运行成本。正如我们将在实验中展示的,批量删除显著降低了更新成本。
我们进一步提供了一个示例来说明批处理插入和删除如何支持更方便的更新。由于空间的限制,我们将其留在完整版本的技术报告中。
时间的复杂性假设有吗?成批处理中的更新。如果它们都是插入,那么批插入的时间复杂度是? 2 |2Λ| · ?· (|???| · ?+ |?| · (?+ ?)),,它与第3.1节中的单个插入相同)。但是,请注意,受感染节点的数量为|????这些批处理中的|往往比单个插入的|要大得多。此外,请注意,在最坏的情况下,|????= ?|,我们的时间复杂度与指数重建具有相同的时间复杂度。同样,批处理删除的时间复杂度是?|吗?|·(|Λ| +日志吗?)+ |?| · 2 2|Λ| · ? (?+ ?),,这与第3.2节中的单次删除相同)。
4.3 Dealing with Large-Label Graphs
为了自包含,我们简要回顾一下P2H+如何处理大型标签,然后说明如何集成到DLCR中以及如何动态更新索引。为了处理具有大量标签的图,P2H+引入了一个两级索引方案,其中包括一个主索引和一个二级索引。主要索引包括从标签集Λ中选择的频繁标签的小集合Λ‘。然后,在只包含边的子图上处理标签来自Λ‘的边。在P2H+中,Λ‘的大小设置为6,并选择频率最高的6个标签。对于辅助索引,它的frst是将Λ\Λ‘中的所有标签映射到虚拟标签的|Λ’|数。主索引中使用的标签的映射与次级索引中的映射一致。因此,在P2H+中,虚拟标签的数量也是6个。然后,在虚拟标签上构建索引。给定一个查询来自?向通过标签集Ψ,它用主索引进行查询,并查看是否?可以到达吗?通过Ψ∩Λ‘。如果答案是肯定的,那么它会立即返回为真。否则,它将使用辅助索引进行查询。如果辅助索引返回false,则查询可以返回false。否则,它将进行LC-BFS在线获取查询答案。在我们的更新算法中,我们将使用完全相同的DLCR插入和删除算法来更新主索引和次索引。
5 EXPERIMENTS
5.1 Experimental Setup
设置。我们在C++中实现了所有的算法,并使用g++进行完全优化编译。P2H+的源代码由其发明者[21]提供。所有实验都是在一台拥有IntelXeon2.3 GHz CPU和384GB内存的Linux机器上进行的
数据集和查询集。我们在来自不同类型的复杂大型网络的22个真实世界的图数据集上进行了实验,包括社交网络、网络网络、引文网络和生物网络。表5总结了被测试数据集的统计数据。本实验中使用的所有数据集都可以从SNAP[18]和KONECT[17]中公开获得。对于没有边缘标签的数据集,我们按照[21]中的设置以指数分布合成边缘标签。合成标签的数量默认设置为8个。大标签图的数字|Λ‘|默认设置为4。我们比较了假查询和真查询这两种查询。生成策略与[21]相同,我们使用三种类型的标签集数字来生成每种类型的查询,分别是2、4和6。我们为每个标签集编号生成10,000个查询,并计算平均查询时间。
比较算法。我们比较了我们的DLCR,它采用查询友好的动态数组设计,与以下方法: DLCR-BST,它使用二进制搜索树存储索引;到达,动态图上常规路径查询[28]的最先进的近似算法;P2H+,静态图上LCR查询[21]的最先进的2跳索引。
由于空间有限,我们不能将所有的实验结果都纳入本文中。额外的实验结果和讨论包含在我们的完整版本的技术报告中,它可以在我们的源代码存储库中找到。附加的实验检查了更多的查询工作负载,图密度和标签大小的数量对DLCR更新和查询性能的影响,当更新比索引重建更方便时,虚拟标签的数量的影响,以及在混合工作负载下的性能。
5.2 Experimental Comparisons
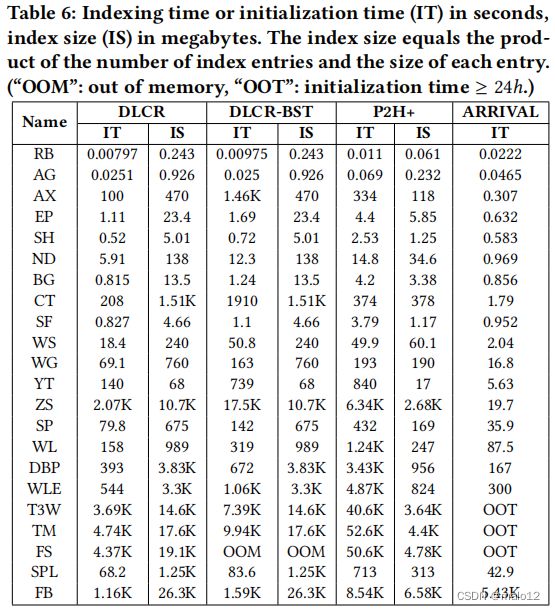
经验1:索引成本。如表6所示,DLCR的指数构建时间比P2H+小约一个数量级,平均比DLCR-BST小近2倍。这主要是由于我们的DLCR索引的查询友好设计,降低了查询成本,如表7所示。在几乎所有的数据集上,DLCR-BST在索引构建上都比P2H+快2倍。主要原因是DLCR-BST对每个???只维护一个BST(?)或(?)而在P2H+中,在???中对不同的节点保持多个bst(?)或(?).
接下来,我们将检查三种方法的索引大小。由于我们在每个索引条目中保留了反向索引和其他额外信息,例如,最后一条边,DLCR的索引大小和DLCRBST大约是P2H+的4倍。此外,ARRIVAl的初始化时间不能忽略,因为它对T3W、TM和FS的初始化不能在24小时内消失,而我们的DLCR在一个半小时内完成所有22个数据集的索引构建。
接下来,我们将检查三种方法的索引大小。由于我们在每个索引条目中保留了反向索引和其他额外信息,例如,最后一条边,DLCR的索引大小和DLCRBST大约是P2H+的4倍。此外,ARRIVAl的初始化时间不能忽略,因为它对T3W、TM和FS的初始化不能在24小时内消失,而我们的DLCR在一个半小时内完成所有22个数据集的索引构建。
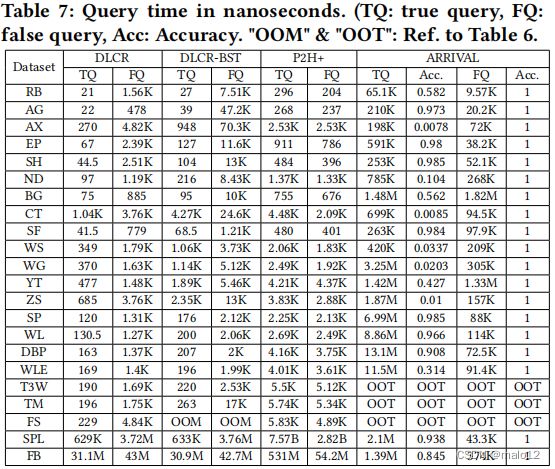
Exp 2:查询性能。对于真正的查询集,表7显示,由于DLCR的查询友好型设计,DLCR在查询处理方面几乎比P2H+快了一个数量级。DLCR-BST仍然比P2H+快2倍左右。DLCR比到达时间快近四个数量级,而DLCR可以给出确切的答案。相比之下,在真实查询上,对于真实标记图(例如RB为58%,BG为56%,YT为43%,FB为85%)和合成生成的标记图(WLE为32%),都可能返回精度较低的近似解。表7还显示了DLCR接近4倍比错误查询集的P2H+更快。在大多数数据集中,DLCR-BST将比P2H+快2倍左右。此外,DLCR比到达的速度快近两个数量级。对于错误的查询,请注意,到达将始终达到100%的准确性。
经验3:删除评估。在这组实验中,从均匀分布中随机选择被删除的边。被删除的边数被设置为10?、20?、40?和80?。对于每个被删除的边数,我们重复10轮,并计算平均删除时间。值得注意的是,即使在像T3W、TM和FS这样的数十亿个边缘图上,我们的更新延迟也可以小到几毫秒(约0.1 ms)。此外,与单边DLCR删除算法相比,我们的批量删除算法显著降低了更新成本。特别是,在AX和CT数据集上,批量删除算法比算法快2个数量级,比单边删除算法快2个数量级。为了解释,这些图是引文网络,并且连接良好,其中一次删除可能需要更新大部分索引。在这种情况下,我们的批删除算法因此避免了大量不必要的更新,并使批删除在这些网络上具有超强的预见性。此外,使用我们的批处理删除算法,平均更新成本总是以几十毫秒为限。
经验4:插入评估。这些设置类似于Exp 3中的设置,其中唯一的区别是我们在Exp 4中插入了删除边。图3表明,单边插入方法和批处理插入方法都是有效的。在大多数数据集中,平均插入时间可以在10−3到10−5秒之间,而批量插入可以提高一个数量级,当集体更新可能帮助,例如引文网络AX和CT。一般来说,DLCR插入算法比删除算法快5倍-10倍;批插入算法比批删除算法快2倍-5倍。
6 RELATED WORK
标签限制可达性(LCR)查询。关于LCR查询的基本工作是由[15]提出。他们引入了一种新的基于树的指数框架,利用有向最大加权生成树算法和采样技术,将标记图的广义传递闭包压缩到最大可能的程度。最先进的索引技术是P2H+,这是一种具有新的剪枝规则和顺序策略[21]的2跳索引。与基于地标索引的算法[26]相比,P2H+具有更小的索引,更好的查询性能。
动态图方法。由于现实世界网络的动态特性,迫切需要开发图问题的全动态解决方案。Fan等人对增量图算法[10]的可行和不可可行进行了理论研究。[19]提出了一种基于有效的局部更新技术的一种有效的分层核心维护算法。这些算法还被扩展到处理批处理中多个插入/删除的边。[9,12,23,24]提出了在动态图上逐步保持传递闭包的算法。然而,这些方法不能扩展到[16]所显示的十亿尺度的图。[5,8,25]提出了更新2跳标记指数的方法。[14,32,33]提出了对可达性索引执行更新的算法。TOL [33]为2跳标记索引提出了增量更新方法,其中TOL侧重于从图中删除或插入一个顶点。然而,这些方法不能扩展到动态图上的LCR查询,这是我们的DLCR的主要贡献。
7 CONCLUSIONS AND FUTURE WORK
在本文中,我们提出了DLCR,一个基于2跳索引的动态图LCR查询框架。大量的实验表明了我们所提出的算法的有效性和有效性。对于未来的工作,我们计划研究设计有效的索引构建并行算法和更新算法。