PageRank总结&python实现

本文将记录在学习pagerank的有关内容，如果您也在做相关的工作请与我邮件沟通交流 [email protected]

pagerank理论及推导

pagerank算法是对于在一个有向图上，找到每个节点的重要性程度，最终得到每个节点的重要性打分。

在实际使用中是为了找到在网页上网页的重要性程度，由于pagerank算法是单纯的和图网络结构相关，所以他是与主题无关的离线算法。

PageRank算法的思路是，对于图(网络)上的每个节点(一个具体的网页)设置一个重要性初始值，每个节点的重要性程度会平均的分给由该节点的出度节点，每个节点的重要性程度也是由该节点的所有分给她的入度节点重要性的求和。那么问题就变成了由当前的状态通过转移的方法获得更新状态的马尔科夫链的过程。

定义些相关的符号：

• N 全部的节点个数
• $O_i$节点i的出度个数
• $P{R}_i$ 节点i的PageRank得分，全部的节点的PR得分是一个长度为N的向量 PR
• $d$ 阻尼系数

由之前的定义可以得到，每个节点的PR得分由该节点的入度所赋予的PR的和

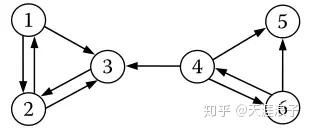
如图中所示

$$P{R}_2=P{R}_1/2+P{R}_3/1+0P{R}_4+0P{R}_5+0P{R}_6$$
整理得到
$$P{R}_2=[1/2,0,1,0,0,0]\ast PR$$
其中的[1/2,0,1,0,0,0]是节点2的在图上的入度情况，每个值是节点2的入度列表除以对应节点的总的出度数。
具体而言节点2的入度列表应该是[1,0,1,0,0,0]，其中1代表所在位置的节点对节点2是有出度的(1,3有出度到2),然后每个入度列表在以此的除以每个节点上的出度数[2,2,1,3,0,2],其中每个数是对应位置上的出度数，两个列表对应位置相除得到了对于节点2来说他的入度转移向量。我们把所有节点的入度转移向量拼接起来得到该图的入度转移矩阵A

以上这个图片是从知乎复制过来的，他的定义和上文我的定义不一样，
在图片中每一行是对应节点的出度，每一列是对应节点的入度
所以按照上文我的定义来看，是需要将这个矩阵转置之后在来进行计算的
在接下来的描述中，为了方便起见，所有的矩阵都按照图片的为主，在计算时会添加转置

在得到了转移矩阵后，就得到了一个马尔科夫链的计算过程
$$P{R}_{new}=A^T\ast P{R}_{old}$$
设置一个PR的初始状态，一般是把所有节点的初始值设置为1，那么就可以进入循环中以此找到新的PR值向量。当$|P{R}_{new}-P{R}_{old}|<阈值$的时候结束循环将最后的PR作为最终的PR结果。

以上内容就是理想状态下的PageRank算法，现在我们考虑下实际情况。

假设在图中存在一个独立的环，也就是存在一个0>1>2>0的循环结构，且环上的每个节点有且仅有一个入度和出度，那么按照理想状态下的PageRank算法，这样的环会无限的循环下去无法跳出去。为了防止这样的情况发生，设置一个阻尼系数，意义是从一个节点按照链接方式链接到另外一个节点的概率，一般设置为0.85，具体而言也就是当0>1,节点0到节点1之间存在一个有向的链接，那么从0到1的会按照阻尼系数0.85的概率进行跳转。对于每个节点的初始选择按照 $（1-d）/N$的比例进行选择，那么上面的PR的公式就要进行修改，

$$P{R}_2=d\ast （P{R}_1/2+P{R}_3/1)+（1-d）/N$$

按照修改之后的PR计算公式就需要重新修改转移矩阵A

$$A_{new}=d\ast A_{old}+(1-d)/N\ast e\ast e^T$$

其中e是一个长度为N的全是1的向量，那么$e\ast e^T$就是一个N*N的方阵，这个方阵内全是1.
具体的计算没有发生变化，依旧是按照马尔科夫过程
$$P{R}_{new}=A^T\ast P{R}_{old}$$
其中A的每一行为出度，每一列是入度。
至此，实际使用中的PageRank算法就推导完了。

计算

有三种计算方法

1. 迭代法
   按照马尔科夫的迭代过程一直循环直到差值小于阈值
2. 特征向量法
   P=AP，显然P的A特征值为1时的特征向量
3. 代数计算
   

PageRank涉及到的数学内容

马尔科夫过程

pagerank的python实现

参考网页链接

https://www.cnblogs.com/rubinorth/p/5799848.html
https://blog.csdn.net/lingerlanlan/article/details/46991167
https://zhuanlan.zhihu.com/p/20201748
https://zhuanlan.zhihu.com/p/44279297