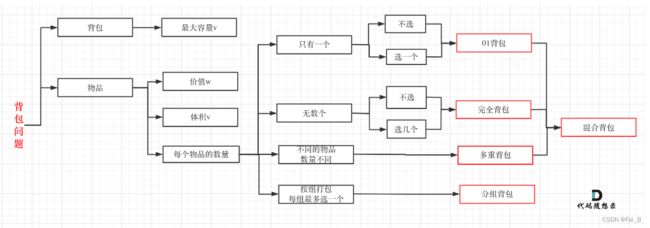
Backpack problems 416. Partition Equal Subset Sum

 01 backpack

There are n objects and a backpack that can carry at most w weights. The weight of the ith object is weight[i] and the value obtained is value[i] . Each object can be used only once, so solve for which objects to put in the backpack that have the greatest sum of values.

1. 1. dp[i][j]:  represents the maximum sum of values of any objects taken from [0-i] and put into the backpack of capacity j.

2. nothing put in: dp[i][j] = dp[i - 1][j] , cuz weight[i] > j

    object put in : dp[i][j] = dp[i - 1][j - weight[i]] + value[i]

3. recurrence formula :  dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

4.initialization: if j == 0:    dp[i][0] = 0

                          if j < weight[0]:   dp[0][j] = 0  elif j >= weight[0]:  dp[0][j] = value[0]

5. Traverse the item first or the pack weight first? 

both is ok,  traverse the item first is better to understand!

// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

    }
}

---------------------------------------------------------------------------------------------------------------------------------

---------------------------------------------------------------------------------------------------------------------------------

一维dp数组（滚动数组）

One-dimensional dp arrays (rolling arrays)

In fact, it can be found that if the layer dp[i - 1] is copied onto dp[i], the expression could well be: dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]); 

1. dp[j] denotes: a backpack with capacity j. The value of the items carried can be maximized to dp[j].

2.recurrence formula :

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); #不同的i对应同一个j时候

3.initialization

dp[0] = 0

4.One-dimensional dp array traversal order

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

 The reverse order traversal is to ensure that item i is only put in once! But if once it is traversed in positive order, then item 0 will be rejoined multiple times!

---------------------------------------------------------------------------------------------------------------------------------

---------------------------------------------------------------------------------------------------------------------------------

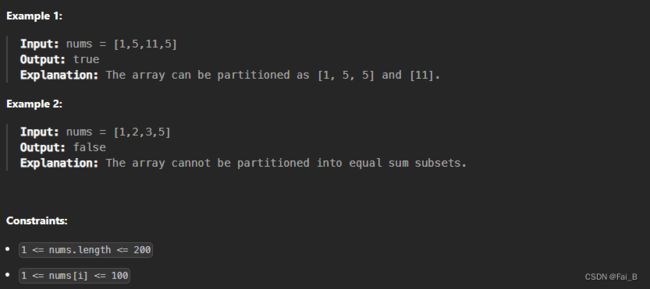
416. Partition Equal Subset Sum

Given an integer array nums, return true if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or false otherwise.

 1-dimensional dp arrays:

 recurrence formula :  dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])    weight == value in this problem

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        if sum(nums) % 2 != 0:
            return False
        target = sum(nums) // 2
        dp = [0] * (target + 1)
        for num in nums:
            for j in range(target, num-1, -1):
                dp[j] = max(dp[j], dp[j-num] + num)
        return dp[-1] == target

2-dimensional dp arrays:

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        
        total_sum = sum(nums)

        if total_sum % 2 != 0:
            return False

        target_sum = total_sum // 2
        dp = [[False] * (target_sum + 1) for _ in range(len(nums) + 1)]

        # 初始化第一行（空子集可以得到和为0）
        for i in range(len(nums) + 1):
            dp[i][0] = True

        for i in range(1, len(nums) + 1):
            for j in range(1, target_sum + 1):
                if j < nums[i - 1]:
                    # 当前数字大于目标和时，无法使用该数字
                    dp[i][j] = dp[i - 1][j]
                else:
                    # 当前数字小于等于目标和时，可以选择使用或不使用该数字
                    dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i - 1]]

        return dp[len(nums)][target_sum]