121. Best Time to Buy and Sell Stock 122. Best Time to Buy and Sell Stock II
121. Best Time to Buy and Sell Stock
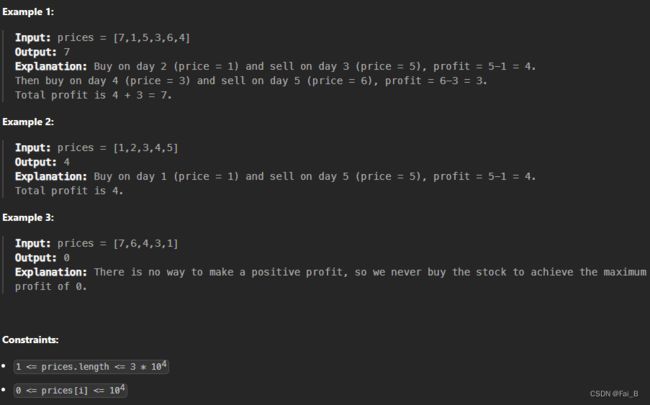
You are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
AC 1-dimensional DP:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
dp = [0] * (len(prices))
start = prices[0]
for i in range(1, len(prices)):
if prices[i] - start > dp[i - 1]:
dp[i] = prices[i] - start
else:
dp[i] = dp[i - 1]
start = min(start, prices[i])
return dp[-1]
2-dimensional DP:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
length = len(prices)
if len == 0:
return 0
dp = [[0] * 2 for _ in range(length)]
dp[0][0] = -prices[0]
dp[0][1] = 0
for i in range(1, length):
dp[i][0] = max(dp[i-1][0], -prices[i])
dp[i][1] = max(dp[i-1][1], prices[i] + dp[i-1][0])
return dp[-1][1]2-dimensional DP optimal:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
length = len(prices)
dp = [[0] * 2 for _ in range(2)] #注意这里只开辟了一个2 * 2大小的二维数组
dp[0][0] = -prices[0]
dp[0][1] = 0
for i in range(1, length):
dp[i % 2][0] = max(dp[(i-1) % 2][0], -prices[i])
dp[i % 2][1] = max(dp[(i-1) % 2][1], prices[i] + dp[(i-1) % 2][0])
return dp[(length-1) % 2][1]greedy approch:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
low = float("inf")
result = 0
for i in range(len(prices)):
low = min(low, prices[i]) #取最左最小价格
result = max(result, prices[i] - low) #直接取最大区间利润
return result122. Best Time to Buy and Sell Stock II
You are given an integer array prices where prices[i] is the price of a given stock on the ith day.
On each day, you may decide to buy and/or sell the stock. You can only hold at most one share of the stock at any time. However, you can buy it then immediately sell it on the same day.
Find and return the maximum profit you can achieve.
dp[i][0] is the maximum net profit(净利润) from holding the stock on day i.
dp[i][1] is the large net profit from not holding stocks on day i
greedy approch:
Time complexity: O(n)
Space complexity: O(1)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
result = 0
for i in range(1, len(prices)):
if prices[i] - prices[i-1] > 0:
result += prices[i] - prices[i-1]
return result
2-dimensional DP:
Time complexity: O(n)
Space complexity: O(n)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
dp = [[0, 0] for _ in range(len(prices))]
dp[0][0] = -prices[0] #第0天持有股票
dp[0][1] = 0 #第0天没持有股票
for i in range(1, len(prices)):
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])# 第i天持有股票:1.第i天没买之前买的 2.第i-1天没持股票,第i天买入
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i])# 第i天没持有股票:1.第i-1天也没持有股票 2.第i-1天持有股票,第i天卖掉
return dp[-1][1]Space optimal:
Time complexity: O(n)
Space complexity: O(1)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
length = len(prices)
dp = [[0] * 2 for _ in range(2)] #注意这里只开辟了一个2 * 2大小的二维数组
dp[0][0] = -prices[0]
dp[0][1] = 0
for i in range(1, length):
dp[i % 2][0] = max(dp[(i-1) % 2][0], dp[(i-1) % 2][1] - prices[i])
dp[i % 2][1] = max(dp[(i-1) % 2][1], dp[(i-1) % 2][0] + prices[i])
return dp[(length-1) % 2][1]