【c++算法篇】--30分钟从0到精通讲解算法--搜索
c++搜索算法---详解
- 搜索算法概念
- 具体实现
-
- 深度优先搜索(dfs)
-
- 原理/思路
- 实现过程
-
- 例题
-
- 题目1
- 题目2
- 题目3
- 题目4
- AC代码+思路详解
-
- 题目1
- 题目2
- 题目3
- 题目4
- 广度优先搜索(bfs)
-
- 原理/思路
- 实现过程
-
- 例题
-
- 题目1
- 题目2
- 题目3
- AC代码+思路详解
-
- 题目1
- 题目2
- 题目1
- 总结:
-
- 答疑解惑
-
-
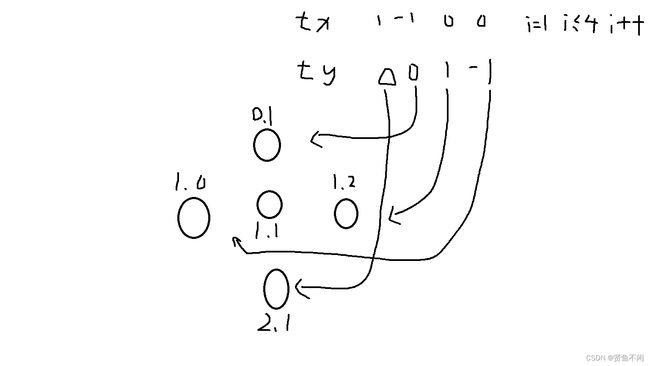
- 方向数组
-
搜索是c语言中重要的算法之一,为以后的学习打下了基础,下面让我们来了解一下:

搜索算法概念
是通过进行递归操作或者通过队列的特殊性质来进行解题的一种算法,具体分为深度优先搜索(dfs)和广度优先搜索(bfs),在具体解决题目的过程中可以通过题目来选择不同的解法,在数据范围允许的情况下,两种方式可以进行互相转换,下面会进行具体介绍。
具体实现
深度优先搜索(dfs)
是以深度为优先的搜索方式,在一些数据范围不大的走迷宫类型的题目中可以运用,通过不停的试错的方式找寻答案,但是有可能会mle
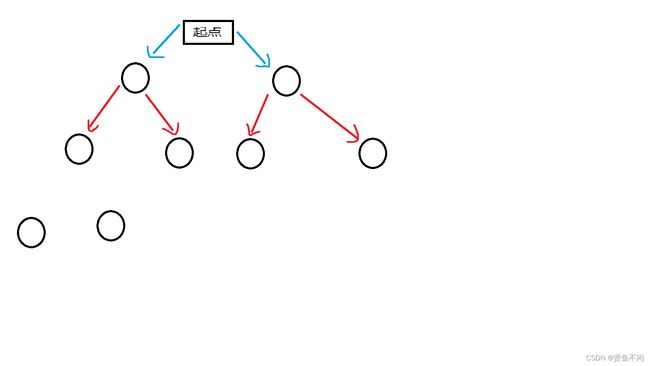
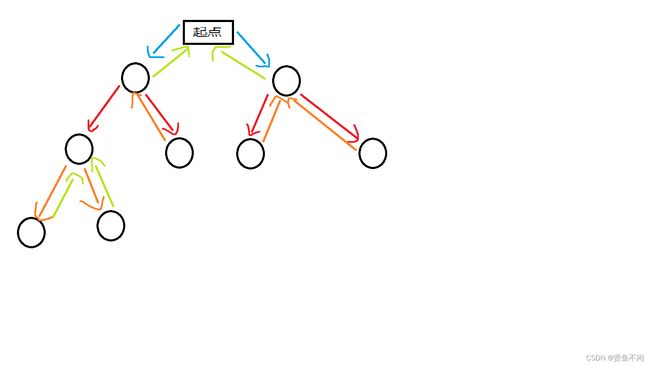
原理/思路
如下




后面以此类推
所以深度搜索就是依靠递归操作寻找答案。
注意:
题目如果数据范围过大不建议使用,很有可能可以找到答案,但是需要大量时间(实在没有办法就打表吧。)
实现过程
先来看到题
<<
放苹果:
描述
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
输入
第一行是测试数据的数目t(0 <= t <= 20)。以下每行均包含二个整数M和N,以空格分开。1<=M,N<=10。
输出
对输入的每组数据M和N,用一行输出相应的K。
样例输入
1
7 3
样例输出
8
>>
有没有感到熟悉
直接上代码
#include现在是不是对深度优先搜索有了一个初步认识了,下面来总结一下
void dfs(按照题目要求传入参数){
if(判断结束条件){
****
return ;
}
for(继续处理){
dfs(进行递归);
}
}
模板总结完毕,下面来实操一下
例题
题目1
题目如下:
8465:马走日
总时间限制: 1000ms 内存限制: 65536kB
描述
马在中国象棋以日字形规则移动。
请编写一段程序,给定n*m大小的棋盘,以及马的初始位置(x,y),要求不能重复经过棋盘上的同一个点,计算马可以有多少途径遍历棋盘上的所有点。
输入
第一行为整数T(T < 10),表示测试数据组数。
每一组测试数据包含一行,为四个整数,分别为棋盘的大小以及初始位置坐标n,m,x,y。(0<=x<=n-1,0<=y<=m-1, m < 10, n < 10)
输出
每组测试数据包含一行,为一个整数,表示马能遍历棋盘的途径总数,0为无法遍历一次。
样例输入
1
5 4 0 0
样例输出
32
提示:可以从棋盘大小,马下一步的移动位置思考
题目2
题目如下:
1789.算24
描述
给出4个小于10个正整数,你可以使用加减乘除4种运算以及括号把这4个数连接起来得到一个表达式。现在的问题是,是否存在一种方式使得得到的表达式的结果等于24。
这里加减乘除以及括号的运算结果和运算的优先级跟我们平常的定义一致(这里的除法定义是实数除法)。
比如,对于5,5,5,1,我们知道5 * (5 – 1 / 5) = 24,因此可以得到24。又比如,对于1,1,4,2,我们怎么都不能得到24。
输入
输入数据包括多行,每行给出一组测试数据,包括4个小于10个正整数。最后一组测试数据中包括4个0,表示输入的结束,这组数据不用处理。
输出
对于每一组测试数据,输出一行,如果可以得到24,输出“YES”;否则,输出“NO”。
样例输入
5 5 5 1
1 1 4 2
0 0 0 0
样例输出
YES
NO
提示:可以将所有的操作都递归进去
题目3
题目如下:
1818.红与黑
描述
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻的黑色瓷砖移动。请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入
包括多个数据集合。每个数据集合的第一行是两个整数W和H,分别表示x方向和y方向瓷砖的数量。W和H都不超过20。在接下来的H行中,每行包括W个字符。每个字符表示一块瓷砖的颜色,规则如下
1)‘.’:黑色的瓷砖;
2)‘#’:红色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
输出
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
样例输入
6 9
…#.
…#
…
…
…
…
…
#@…#
.#…#.
0 0
样例输出
45
提示:普通的走迷宫,稍加判断位置即可
题目4
题目如下:
1805:碎纸机
描述
你现在负责设计一种新式的碎纸机。一般的碎纸机会把纸切成小片,变得难以阅读。而你设计的新式的碎纸机有以下的特点:
1.每次切割之前,先要给定碎纸机一个目标数,而且在每张被送入碎纸机的纸片上也需要包含一个数。
2.碎纸机切出的每个纸片上都包括一个数。
3.要求切出的每个纸片上的数的和要不大于目标数而且与目标数最接近。
举一个例子,如下图,假设目标数是50,输入纸片上的数是12346。碎纸机会把纸片切成4块,分别包含1,2,34和6。这样这些数的和是43 (= 1 + 2 + 34 + 6),这是所有的分割方式中,不超过50,而又最接近50的分割方式。又比如,分割成1,23,4和6是不正确的,因为这样的总和是34 (= 1 + 23 + 4 + 6),比刚才得到的结果43小。分割成12,34和6也是不正确的,因为这时的总和是52 (= 12 + 34 + 6),超过了50。
还有三个特别的规则:
1.如果目标数和输入纸片上的数相同,那么纸片不进行切割。
2.如果不论怎样切割,分割得到的纸片上数的和都大于目标数,那么打印机显示错误信息。
3.如果有多种不同的切割方式可以得到相同的最优结果。那么打印机显示拒绝服务信息。比如,如果目标数是15,输入纸片上的数是111,那么有两种不同的方式可以得到最优解,分别是切割成1和11或者切割成11和1,在这种情况下,打印机会显示拒绝服务信息。
为了设计这样的一个碎纸机,你需要先写一个简单的程序模拟这个打印机的工作。给定两个数,第一个是目标数,第二个是输入纸片上的数,你需要给出碎纸机对纸片的分割方式。
输入
输入包括多组数据,每一组包括一行。每行上包括两个正整数,分别表示目标数和输入纸片上的数。已知输入保证:两个数都不会以0开头,而且两个数至多都只包含6个数字。
输入的最后一行包括两个0,这行表示输入的结束。
输出
对每一组输入数据,输出相应的输出。有三种不同的输出结果:
sum part1 part2 …
rejected
error
第一种结果表示:
1.每一个partj是切割得到的纸片上的一个数。partj的顺序和输入纸片上原始数中数字出现的次序一致。
2.sum是切割得到的纸片上的数的和,也就是说:sum = part1 + part2 +…
第一种结果中相邻的两个数之间用一个空格隔开。
如果不论怎样切割,分割得到的纸片上数的和都大于目标数,那么打印“error”。
如果有多种不同的切割方式可以得到相同的最优结果,那么打印“rejected”。
样例输入
50 12346
376 144139
927438 927438
18 3312
9 3142
25 1299
111 33333
103 862150
6 1104
0 0
样例输出
43 1 2 34 6
283 144 139
927438 927438
18 3 3 12
error
21 1 2 9 9
rejected
103 86 2 15 0
rejected
提示:读题
AC代码+思路详解
题目1
题解如下:
#include题目2
题解如下:
#include题目3
题解如下:
#include题目4
题解如下:
#include广度优先搜索(bfs)
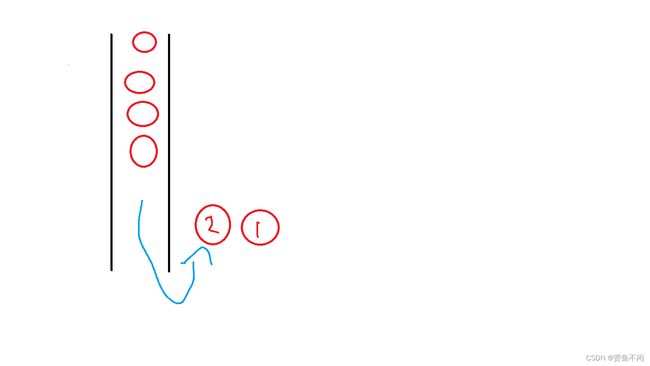
由此可见:队列的是先进先出
原理/思路
实现过程
老规矩看到题
<<
2753:走迷宫
总时间限制: 1000ms 内存限制: 65536kB
描述
一个迷宫由R行C列格子组成,有的格子里有障碍物,不能走;有的格子是空地,可以走。
给定一个迷宫,求从左上角走到右下角最少需要走多少步(数据保证一定能走到)。只能在水平方向或垂直方向走,不能斜着走。
输入
第一行是两个整数,R和C,代表迷宫的长和宽。( 1<= R,C <= 40)
接下来是R行,每行C个字符,代表整个迷宫。
空地格子用’.‘表示,有障碍物的格子用’#‘表示。
迷宫左上角和右下角都是’.'。
输出
输出从左上角走到右下角至少要经过多少步(即至少要经过多少个空地格子)。计算步数要包括起点和终点。
样例输入
5 5
…###
#…
#.#.#
#.#.#
#.#…
样例输出
9
>>
上代码
#include现在是不是对深度优先搜索有了一个初步认识了,下面来总结一下
void bfs(){
push//入队
while(empty){
front//取出队首元素
pop出队
for(循环处理){
if(判断不符合题意条件) continue;
push//入队新元素
if(判断结束条件){
}
}
}
}
例题
题目1
题目如下:
2727:仙岛求药
总时间限制: 1000ms 内存限制: 65536kB
描述
少年李逍遥的婶婶病了,王小虎介绍他去一趟仙灵岛,向仙女姐姐要仙丹救婶婶。叛逆但孝顺的李逍遥闯进了仙灵岛,克服了千险万难来到岛的中心,发现仙药摆在了迷阵的深处。迷阵由M×N个方格组成,有的方格内有可以瞬秒李逍遥的怪物,而有的方格内则是安全。现在李逍遥想尽快找到仙药,显然他应避开有怪物的方格,并经过最少的方格,而且那里会有神秘人物等待着他。现在要求你来帮助他实现这个目标。
下图 显示了一个迷阵的样例及李逍遥找到仙药的路线.
输入
输入有多组测试数据. 每组测试数据以两个非零整数 M 和 N 开始,两者均不大于20。M 表示迷阵行数, N 表示迷阵列数。接下来有 M 行, 每行包含N个字符,不同字符分别代表不同含义:
- ‘@’:少年李逍遥所在的位置;
- ‘.’:可以安全通行的方格;
- ‘#’:有怪物的方格;
- ‘’:仙药所在位置。
当在一行中读入的是两个零时,表示输入结束。
输出
对于每组测试数据,分别输出一行,该行包含李逍遥找到仙药需要穿过的最少的方格数目(计数包括初始位置的方块)。如果他不可能找到仙药, 则输出 -1。
样例输入
8 8
.@##…#
#…#.#
#.#.##…
…#.###.
#.#…#.
…###.#.
…#.…
.#…###
6 5
..#.
.#…
…##.
…
.#…
…@
9 6
.#…#.
.#..#
.####.
…#…
…#…
…#…
…#…
#.@.##
.#…#.
0 0
样例输出
10
8
-1
提示:见例题
题目2
题目如下:
7218:献给阿尔吉侬的花束
总时间限制: 100ms 内存限制: 65536kB
描述
阿尔吉侬是一只聪明又慵懒的小白鼠,它最擅长的就是走各种各样的迷宫。今天它要挑战一个非常大的迷宫,研究员们为了鼓励阿尔吉侬尽快到达终点,就在终点放了一块阿尔吉侬最喜欢的奶酪。现在研究员们想知道,如果阿尔吉侬足够聪明,它最少需要多少时间就能吃到奶酪。
迷宫用一个R×C的字符矩阵来表示。字符S表示阿尔吉侬所在的位置,字符E表示奶酪所在的位置,字符#表示墙壁,字符.表示可以通行。阿尔吉侬在1个单位时间内可以从当前的位置走到它上下左右四个方向上的任意一个位置,但不能走出地图边界。
输入
第一行是一个正整数T(1 <= T <= 10),表示一共有T组数据。
每一组数据的第一行包含了两个用空格分开的正整数R和C(2 <= R, C <= 200),表示地图是一个R×C的矩阵。
接下来的R行描述了地图的具体内容,每一行包含了C个字符。字符含义如题目描述中所述。保证有且仅有一个S和E。
输出
对于每一组数据,输出阿尔吉侬吃到奶酪的最少单位时间。若阿尔吉侬无法吃到奶酪,则输出“oop!”(只输出引号里面的内容,不输出引号)。每组数据的输出结果占一行。
样例输入
3
3 4
.S…
###.
…E.
3 4
.S…
.E…
…
3 4
.S…
.####
…E.
样例输出
5
1
oop!
题目3
题目如下:
6044:鸣人和佐助
查看提交统计提问
总时间限制: 1000ms 内存限制: 65536kB
描述
佐助被大蛇丸诱骗走了,鸣人在多少时间内能追上他呢?
已知一张地图(以二维矩阵的形式表示)以及佐助和鸣人的位置。地图上的每个位置都可以走到,只不过有些位置上有大蛇丸的手下,需要先打败大蛇丸的手下才能到这些位置。鸣人有一定数量的查克拉,每一个单位的查克拉可以打败一个大蛇丸的手下。假设鸣人可以往上下左右四个方向移动,每移动一个距离需要花费1个单位时间,打败大蛇丸的手下不需要时间。如果鸣人查克拉消耗完了,则只可以走到没有大蛇丸手下的位置,不可以再移动到有大蛇丸手下的位置。佐助在此期间不移动,大蛇丸的手下也不移动。请问,鸣人要追上佐助最少需要花费多少时间?
输入
输入的第一行包含三个整数:M,N,T。代表M行N列的地图和鸣人初始的查克拉数量T。0 < M,N < 200,0 ≤ T < 10
后面是M行N列的地图,其中@代表鸣人,+代表佐助。*代表通路,#代表大蛇丸的手下。
输出
输出包含一个整数R,代表鸣人追上佐助最少需要花费的时间。如果鸣人无法追上佐助,则输出-1。
样例输入
样例输入1
4 4 1
#@##
**##
###+
样例输入2
4 4 2
#@##
**##
样例输出
样例输出1
6
样例输出2
4
AC代码+思路详解
题目1
题解如下:
典型走迷宫,自己领悟一下;
#include题目2
题解如下:
#include题目1
题解如下:
#include总结:
通过以上题目和介绍,想必各位对搜索有了基本的认识,在使用过程中也要注意两种方式的互相转换,对于搜索题,大部分都是套模板,但是各位还需要清楚了解搜索的原理和实现过程,今天的介绍到此结束,谢谢大家。
都看到这里了,三联关注一下?嘻嘻^ ^