【LeetCode】105. 从前序与中序遍历序列构造二叉树，106. 从中序与后序遍历序列构造二叉树，144. 二叉树的前序遍历非递归实现，94. 二叉树的中序遍历非递归实现，145. 二叉树的后序

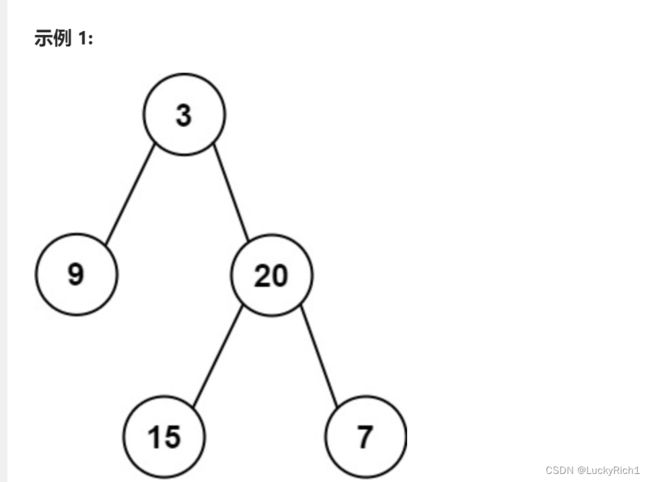
105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

解题思路及实现

class Solution {
public:
    //prei必须是一个引用，不然递归返回的prei还是上一层的prei
    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,int& prei,int inbegin,int inend)
     {
        //缺少了递归返回条件，下面分析一下
        
         TreeNode* root=new TreeNode(preorder[prei]);

        //找到根的左右子树区间
         int rooti=inbegin;//根是会变得，因此不能赋值为0
         while(rooti <= inend)
         {
             if(inorder[rooti] == preorder[prei])
                break;

            ++rooti;
         }

        //递归下一层之前都要向前+1找根
        ++prei;

        //[inbegin rooti-1] rooti [rooti inend]
        root->left=_buildTree(preorder,inorder,prei,inbegin,rooti-1);
        root->right=_buildTree(preorder,inorder,prei,rooti+1,inend);
        return root;
     }


    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {       
        int prev=0;
        return _buildTree(preorder,inorder,prev,0,inorder.size()-1);

    }
};

class Solution {
public:
    //prei必须是一个引用，不然递归返回的prei还是上一层的prei
    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,int& prei,int inbegin,int inend)
     {
        if(inbegin > inend)
            return nullptr;
            
         TreeNode* root=new TreeNode(preorder[prei]);

        //找到根的左右子树区间
         int rooti=inbegin;//根是会变得，因此不能赋值为0
         while(rooti <= inend)
         {
             if(inorder[rooti] == preorder[prei])
                break;

            ++rooti;
         }

        //递归下一层之前都要向前+1找根
        ++prei;

        //[inbegin rooti-1] rooti [rooti inend]
        root->left=_buildTree(preorder,inorder,prei,inbegin,rooti-1);
        root->right=_buildTree(preorder,inorder,prei,rooti+1,inend);
        return root;
     }


    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {       
        int prev=0;
        return _buildTree(preorder,inorder,prev,0,inorder.size()-1);

    }
};

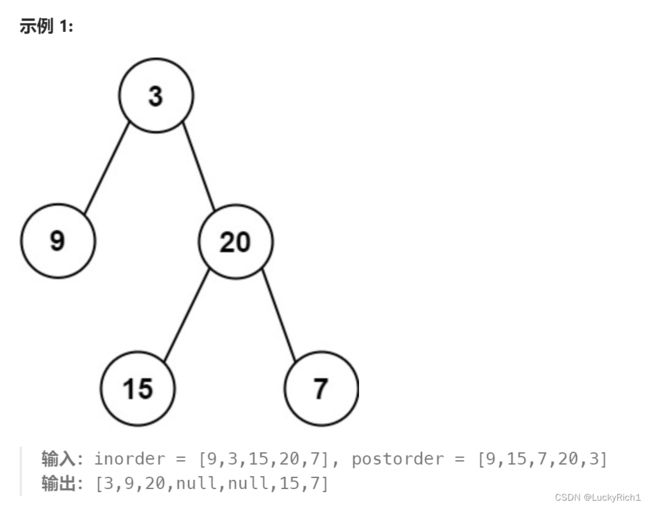
106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

解题思路及实现

class Solution {
public:
    TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder,int inbegin,int inend,int& posti) {

        if(inbegin > inend)
            return nullptr;
        
        TreeNode* root=new TreeNode(postorder[posti]);

        int rooti=inbegin;
        while(rooti <= inend)
        {
            if(inorder[rooti] == postorder[posti])
                break;
            
            ++rooti;
        }

        --posti;
        root->right=_buildTree(inorder,postorder,rooti+1,inend,posti);
        root->left=_buildTree(inorder,postorder,inbegin,rooti-1,posti);
        return root;
    
         
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int post=postorder.size()-1;
        return _buildTree(inorder,postorder,0,inorder.size()-1,post);
    }
};

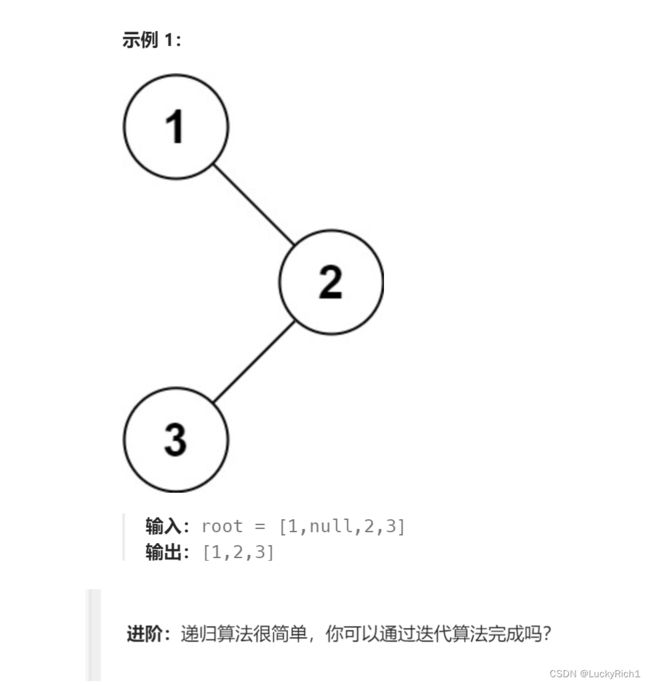
144. 二叉树的前序遍历非递归实现

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

解题思路及实现

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur=root;
        while(cur || !st.empty())
        {
            //左路结点一直进栈
            while(cur)
            {
                v.push_back(cur->val);
                st.push(cur);
                cur=cur->left;
            }

            //出栈，访问它的右子树
            TreeNode* top=st.top();
            st.pop();
            cur=top->right;
        }

        return v;

    }
};

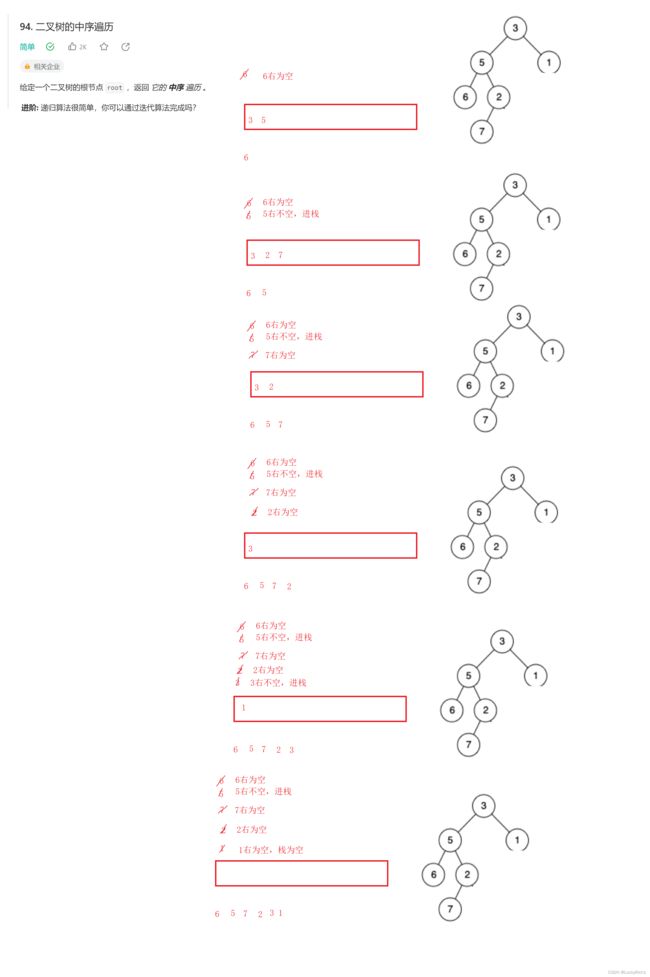
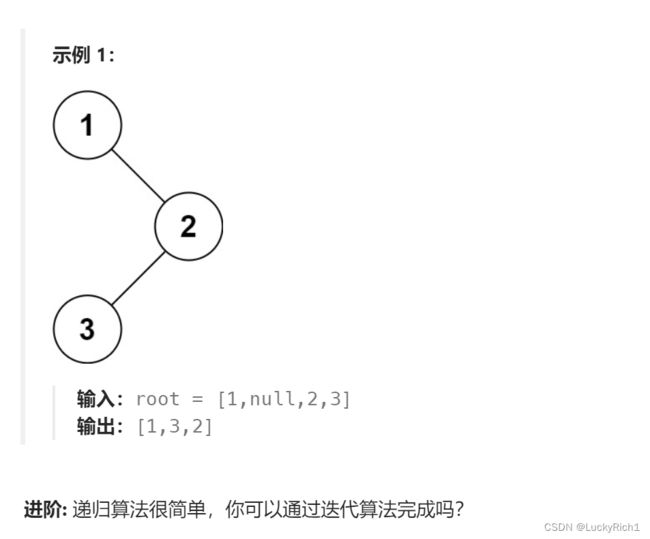
94. 二叉树的中序遍历非递归实现

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

解题思路及实现

中序非递归和前序非递归代码几乎一样，可以自己尝试画图分析一波。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur=root;

        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }

            TreeNode* top=st.top();
            st.pop();
            v.push_back(top->val);

            cur=top->right;
        }
        return v;
    }
};

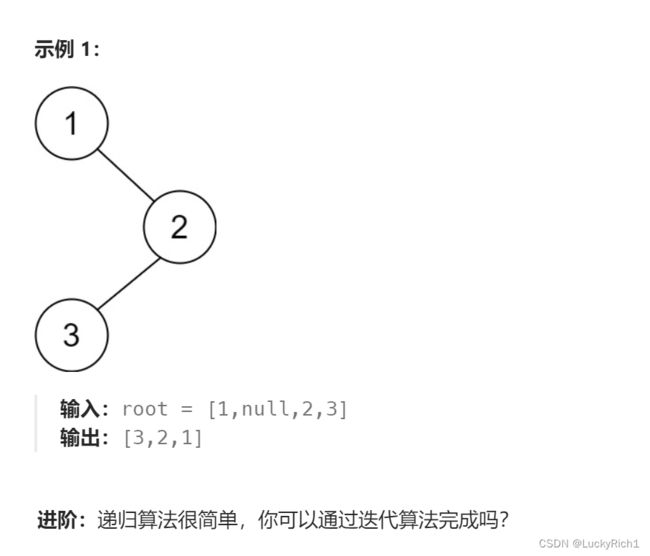
145. 二叉树的后序遍历非递归实现

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

解题思路及实现

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur=root;
        TreeNode* prev=nullptr;
        while(cur || !st.empty())
        {

            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }

            TreeNode* top=st.top();
            //1.top右子树为空，或者右子树不为空且右子树被访问过了(上一个被访问的结点时右子树的根)
            //那就说明右子树不用访问或者被访问过了，直接访问根top
            //2.右子树不为空，且没有被访问，则迭代子问题访问
            if(top->right == nullptr || top->right == prev)
            {
                v.push_back(top->val);
                st.pop();
                prev=top;
            }
            else
            {
                cur=top->right;             
            }

        }
        return v;
    }
};