【数据结构】排序效率最优解之一：二叉树-堆

Hello everybody!今天打算给大家介绍一个功能比较强大的数据结构的基础，它不仅具有很高的应用价值而且排序效率很高。冒泡排序都知道叭，它的时间复杂度为O(n^2)，而堆排序的时间复杂度为O(n*logn)。堆排序直接碾压冒泡排序。在c语言阶段，我曾给过大家qsort函数模拟实现的代码，我是以冒泡排序为底层逻辑实现的：时间复杂度为O(n^2)。而真正库文件中的qsort是以快排为底层逻辑实现的：时间复杂度为O(n*logn)。所以当我们排较长的数值时，肉眼可见的会发现自己模拟实现的qsort的效率远远不及库文件中的qsort。这就很好的体现了时间复杂度为O(n*logn)的数据结构的魅力所在！那好，废话不多说，我们直接开始叭！

1.二叉树的存储结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。

1.顺序结构

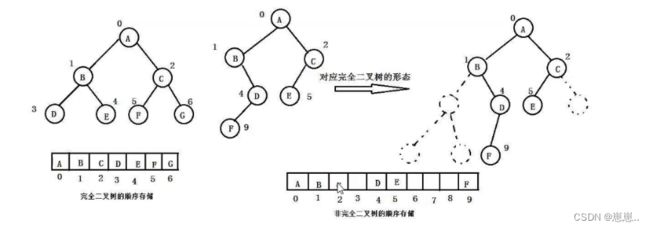
顺序结构存储就是使用数组来存储，一般使用数组只适合完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

2.链式存储

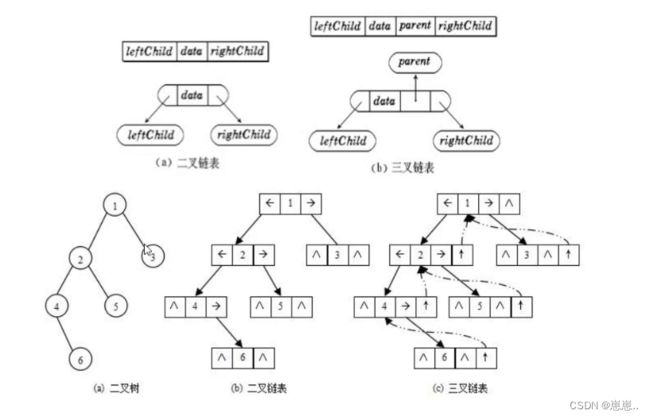
二叉树的链式存储结构是指，用链表来表示一颗二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。链式结构又分为二叉链和三叉链。在当前的知识将借助一般都是二叉链，后面的高阶数据结构如红黑树等会用到三叉链。

2.堆的基本结构

注意堆有大堆和小堆之分。

小堆：每个结点上的数据都比子结点上的数据小，故根结点为最小值。

大堆：每个结点上的数据都比子结点上的数据小，故根结点为最大值。

#pragma once
#include 
#include 
#include 
#include 

typedef int HPDataType;
typedef struct Heap {
	HPDataType* a;
	int size;
	int capacity;
}HP;

这是堆的结构。其中a为数组名，堆上的数全部存放在这个数组中。虽然用数组存放堆，但它们的逻辑结构为堆。

因为：每个父结点的下标*2+1得到其左边的子结点，父结点的下标*2+2得其右边得子结点。

当然也可以反过来推：不管是左边的子结点还是右边的子节点，它们的下标-1与2取整即可得到其父结点。因为小数部分会被省略！

void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);//插入数据并向上调整调整
void HeapPop(HP* php);//删除堆顶（根节点）

int HeapSize(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);

这些是堆需要实现的一些接口。其中最核心的是HeapPush和HeapPop，因为涉及到数据的调整。

其他接口就比较简单，我也就简单介绍一下。

3.接口的实现

那我就按照小堆给大家实现叭！

3.1初始化&销毁

void HeapInit(HP* php) {
	assert(php);//检查php是否为空指针
	php->a = NULL;
	php->size = php->capacity = 0;
}

void HeapDestroy(HP* php) {
	assert(php);
	free(php->a);//将a指向的动态空间还给操作系统
	php->a = NULL;//置空，避免出现野指针
	php->size = php->capacity = 0;
}

这两个接口比较简单，给出的注释比较详细。我就不过多赘述了！

3.2插入数据

void Swap(HPDataType* p1, HPDataType* p2) {
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustUp(HPDataType* a, HPDataType child) {
	int parent = (child - 1) / 2;//找父结点
	while (child > 0) {
		if (a[child] < a[parent]) {//当子结点小于父节点时，交换
			Swap(&a[child], &a[parent]);
			child = (child - 1) / 2;//找上一个子节点
			parent = (parent - 1) / 2;//找上一个父节点
		}
		else {
			break;
		}
	}
}

void HeapPush(HP* php, HPDataType x) {
	assert(php);
	if (php->size == php->capacity) {
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;//当容量等于有效数据时，按二倍扩容
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);//动态开辟空间
		assert(tmp);//检查是否开辟成功
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);//向上调整
}

我大概说一下这个接口的思路：1.首先看到HeapPush,先检查动态数组的容量是否够用，不够用的话就扩容。检查容量过后进入AdjustUp

2.在AdjustUp中，可以通过子节点找父节点，如果不满足小堆的规则，那么父节点的数值和子节点的数值交换，然后下标继续向上调整。直到子节点的下标为零（到达根结点时）结束。

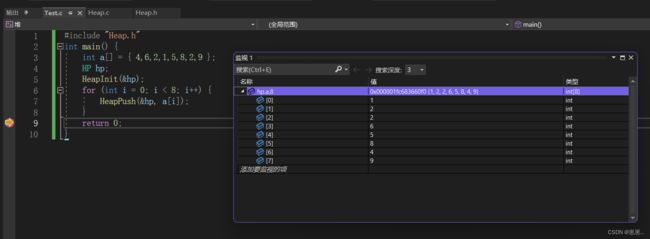
通过调试会发现，确实是一个堆，这个接口的功能正常。

3.3删除堆顶

void AdjustDown(HPDataType* a, int size, int parent) {
	int child = parent * 2 + 1;//通过根结点找子结点
	while (child a[child]) {
			Swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;//继续向下调整
		}
		else {
			break;
		}
	}
}

void HeapPop(HP* php) {
	assert(php);//检查指针
	assert(php->size > 0);//检查有效数据
	Swap(&php->a[0], &php->a[php->size - 1]);//头尾数值交换
	php->size--;//删除最后一个
	AdjustDown(php->a, php->size, 0);//根结点向下调整
}

3.4结点个数&访问根节点&判空

HPDataType HeapTop(HP* php) {
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

int HeapSize(HP* php) {
	assert(php);
	return php->size;
}

bool HeapEmpty(HP* php) {
	assert(php);
	return php->size == 0;
}

这三个接口就很简单啦！宝子们看懂应该没什么问题！

通过测试可以看到堆排序可以实现升序排列，并且效率更高！

4.代码

头文件：

#pragma once
#include 
#include 
#include 
#include 

typedef int HPDataType;
typedef struct Heap {
	HPDataType* a;
	int size;
	int capacity;
}HP;

void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);//插入数据并向上调整调整
void HeapPop(HP* php);//删除堆顶（根节点）

int HeapSize(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);

源文件：

#include "Heap.h"
void HeapInit(HP* php) {
	assert(php);//检查php是否为空指针
	php->a = NULL;
	php->size = php->capacity = 0;
}

void HeapDestroy(HP* php) {
	assert(php);
	free(php->a);//将a指向的动态空间还给操作系统
	php->a = NULL;//置空，避免出现野指针
	php->size = php->capacity = 0;
}
void Swap(HPDataType* p1, HPDataType* p2) {
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustUp(HPDataType* a, HPDataType child) {
	int parent = (child - 1) / 2;//找父结点
	while (child > 0) {
		if (a[child] < a[parent]) {//当子结点小于父节点时，交换
			Swap(&a[child], &a[parent]);
			child = (child - 1) / 2;
			parent = (parent - 1) / 2;
		}
		else {
			break;
		}
	}
}

void HeapPush(HP* php, HPDataType x) {
	assert(php);
	if (php->size == php->capacity) {
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;//当容量等于有效数据时，按二倍扩容
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);//动态开辟空间
		assert(tmp);//检查是否开辟成功
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);//向上调整
}

void AdjustDown(HPDataType* a, int size, int parent) {
	int child = parent * 2 + 1;
	while (child a[child]) {
			Swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else {
			break;
		}
	}
}

void HeapPop(HP* php) {
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

HPDataType HeapTop(HP* php) {
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

int HeapSize(HP* php) {
	assert(php);
	return php->size;
}

bool HeapEmpty(HP* php) {
	assert(php);
	return php->size == 0;
}

测试文件：

#include "Heap.h"
int main() {
	int a[] = { 4,6,2,1,5,8,2,9 };
	HP hp;
	HeapInit(&hp);
	for (int i = 0; i < 8; i++) {
		HeapPush(&hp, a[i]);
	}

	while(!HeapEmpty(&hp)){
		printf("%d", HeapTop(&hp));
		HeapPop(&hp);
	}
	return 0;
}

5.结语

那今天的讨论就到这里喽！不知道大家是否有所收获呢？可以把自己的疑问发在评论区！