Unity中Shader指令优化
文章目录
- 前言
- 解析一下不同运算、条件、函数所需的指令数
-
- 1、常数基本运算
- 2、变量基本运算
- 3、条件语句、循环 和 函数
前言
上一篇文章中,我们解析了Shader解析后的代码。我们在这篇文章中来看怎么实现Shader指令优化
- Unity中Shader指令优化(编译后指令解析)
解析一下不同运算、条件、函数所需的指令数
1、常数基本运算
在DirectX平台,常数运算是不占指令数的。但是,稳妥起见我们最好自己计算好常数计算的结果。防止其他平台认为常数运算需要占指令。
- Shader片元着色器中:
fixed4 frag (v2f i) : SV_Target
{
//常数基本计算
return 2 * 3;
}
- 编译后只有一个赋值给输出结果的指令:
ps_4_0
dcl_output o0.xyzw
0: mov o0.xyzw, l(6.000000,6.000000,6.000000,6.000000)
1: ret
定义临时存储变量,也是不消耗指令数的,对性能没有影响
- Shader片元着色器中:
fixed4 frag (v2f i) : SV_Target
{
//常数基本计算
fixed4 c = 0.2 * 3 / sin(4);
fixed4 c1 = c;
return c1;
}
- 编译后同样只有一个赋值给输出结果的指令:
ps_4_0
dcl_output o0.xyzw
0: mov o0.xyzw, l(-0.792809,-0.792809,-0.792809,-0.792809)
1: ret
2、变量基本运算
变量的基本运算,是会使用GPU计算指令的。因为变量在计算前是未知的,会预留计算指令
- Shader中:
- 属性面板定义一个四维向量
_Value(“Value”,Vector) = (0,0,0,0)
- 片元着色器中,使用该变量进行 加法 计算
fixed4 frag (v2f i) : SV_Target
{
//2、变量基本运算
float a = _Value.x;
float b = _Value.y;
float c = _Value.z;
float d = _Value.w;
float e = 1 + a;
return e;
}
- 编译后(使用了加指令):
ps_4_0
dcl_constantbuffer CB0[3], immediateIndexed
dcl_output o0.xyzw
0: add o0.xyzw, cb0[2].xxxx, l(1.000000, 1.000000, 1.000000, 1.000000)
1: ret
- 变量进行减法运算
e = 1 - a;
- 编译后(使用了加指令):
ps_4_0
dcl_constantbuffer CB0[3], immediateIndexed
dcl_output o0.xyzw
0: add o0.xyzw, -cb0[2].xxxx, l(1.000000, 1.000000, 1.000000, 1.000000)
1: ret
- 变量进行乘法运算(这里测试乘法,别使用 1 或 2,会自动转化为加法)
e = 3 * a
- 编译后(使用了乘指令):
ps_4_0
dcl_constantbuffer CB0[3], immediateIndexed
dcl_output o0.xyzw
0: mul o0.xyzw, cb0[2].xxxx, l(3.000000, 3.000000, 3.000000, 3.000000)
1: ret
- 变量进行除法运算
e = 3 / a
- 编译后(使用了除法指令):
ps_4_0
dcl_constantbuffer CB0[3], immediateIndexed
dcl_output o0.xyzw
0: div o0.xyzw, l(3.000000, 3.000000, 3.000000, 3.000000), cb0[2].xxxx
1: ret
- 变量进行多个相同运算
e = 3 * a * b;
- 编译后:
ps_4_0
dcl_constantbuffer CB0[3], immediateIndexed
dcl_output o0.xyzw
dcl_temps 1
0: mul r0.x, cb0[2].x, cb0[2].y
1: mul o0.xyzw, r0.xxxx, l(3.000000, 3.000000, 3.000000, 3.000000)
2: ret
- 变量进行乘加运算,对性能优化特别重要(特殊)
e = 3 * a + b;
- 编译后,会使用乘加指令(把乘法和加法合并成一个指令)
ps_4_0
dcl_constantbuffer CB0[3], immediateIndexed
dcl_output o0.xyzw
0: mad o0.xyzw, cb0[2].xxxx, l(3.000000, 3.000000, 3.000000, 3.000000), cb0[2].yyyy
1: ret
3、条件语句、循环 和 函数
- 条件语句
if(i.uv.x < 0.5)
{
i.uv.x = 1;
}
else
{
i.uv.x = 0;
}
return i.uv.x;
- 编译后:

这里我们可以使用 step 函数来替代 该 条件语句
替代后,虽然编译结果一样的。但是,这是因为 条件语句 的程序体太简单
如果遇到比较复杂的 条件语句,我们可以使用 结合 step 和 算法的方法 把条件语句剔除
使用 step 函数后:
return step(0.5,i.uv.x);
- 循环语句
float e = 0;
for(int i = 0;i < 5;i++)
{
e += 0.1;
}
return e;
- 编译后:
- mad指令优化:
优化前:
float e = (a + b) * (a - b);
return e;
- 编译后:
float e = a * a * (-b * b);
return e;
- 编译后:
- 透过编译后的代码来直观的看出函数的内部执行(这里使用 normalize 来测试)
一维向量(常数):
float e = normalize(a);
return e;
- 编译后:
float e = normalize(_Value);
return e;
- 编译后:
- abs(如果abs传入的是单一参数,就不会多用指令。但是传入式子,会多用指令)
传入式子:
float e = abs(a * b);
return e;
- 编译后:
float e = abs(a) * abs(b);
return e;
- 编译后:
- 负号可以适当的移到变量中
移动前:
float e = -dot(a,a);
return e;
- 编译后:
移动后:
float e = dot(-a,a);
return e;
- 编译后:
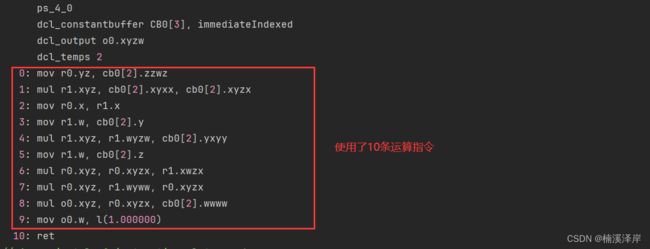
- 尽量把同一维度的向量进行结合运算
结合前:
float3 e = _Value.xyz * a * b * _Value.yzw * c * d;
return fixed4(e,1);
- 编译后:
结合后:
float3 e = (_Value.xyz * _Value.yzw) * (a * b * c * d);
return fixed4(e,1);
- 编译后:
- asin / atan / acos开销很大,尽量不要使用 (这里使用asin测试)
float e = asin(a);
return e;