图的遍历之深度优先(头歌教学实践平台)
第1关:骑士周游问题
任务描述
本关任务:编写代码建立骑士周游图,并解决骑士周游问题。
相关知识
为了完成本关任务,你需要掌握: 1.骑士周游问题的基本概念; 2.如何建立骑士周游图; 3.如何实现骑士周游。
骑士周游问题
骑士周游问题是在国际象棋棋盘上仅用“骑士”这个棋子进行操作。问题的目的是找到一条可以让骑士访问所有格子,并且每个格子只能走一次的走棋序列,把这个走棋序列称为一次“周游”。多年以来,骑士周游问题已经吸引了无数的数学家、棋手和计算机科学家。
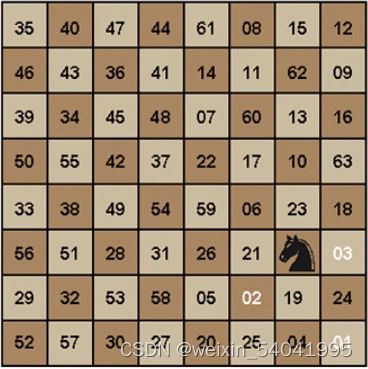
在如图 1 所示 8×8 的国际象棋棋盘上,目前知道的合格的“周游”数量有1.035×这么多。然而,走棋过程中无路可走的情况就更多了。显然,这是一个要么需要真正的智慧,要么占用无数计算资源的问题。![]()
图1 国际象棋棋盘
尽管现在研究人员已经研究了很多不同的算法来解决骑士周游问题,图搜索依旧是最便于理解和编程的算法之一。下面将采用两步走的方案来解决这个问题:
- 将棋盘上合法的走棋次序表示为一个图;
- 采用图搜索算法搜寻一个长度为(
行×列−1)的路径,此路径上包含每个顶点恰好一次。
建立骑士周游图
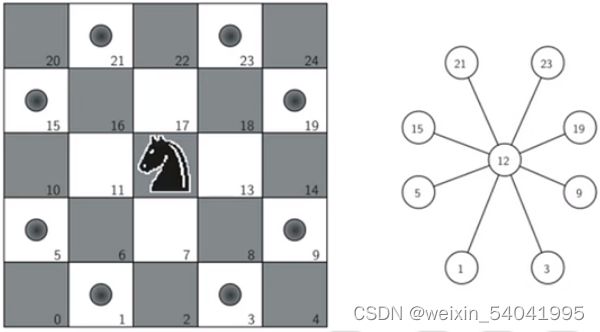
为了将骑士周游问题表示为图,将每个棋盘格作为图的顶点,按照“马走日”规则的走棋步骤作为连接边,建立每一个棋盘格的所有合法走棋步骤能够到达的棋盘格关系图。图 2 展示了骑士合理的走法以及其在图中所对应的边。
图2 在格子 12 上骑士能走的格子以及对应的图
为了建立骑士周游图,需要完成以下方法:
genLegalMoves(x,y,bdSize):作为辅助函数来获取合法走棋位置legalCoord(x,bdSize): 判断骑士是否会走出棋盘边界 bdSizeknightGraph(bdSize): 创建当前这个格子上骑士的所有合法移动列表,返回骑士周游图posToNodeId(row,col,bdSize): 根据棋盘上位置的行列信息转换成一个线性顶点数
图 3 显示了 8×8 棋盘上所有可能的移动方式,图中只有 336 条边。可以看到该图是一个稀疏图,相比全连接时的 4096 条边,只有 8.2% 被填充。
图3 8×8 棋盘上骑士的所有合法走棋步骤
实现骑士周游
用于解决骑士周游问题的图搜索算法是深度优先搜索(Depth First Search),相比前述的广度优先搜索逐层建立搜索树的特点,深度优先搜索是沿着树的单支尽量深入向下搜索,如果到无法继续的程度还未找到问题解,就回溯上一层再搜索下一支。
深度优先搜索解决骑士周游的关键思路是:如果沿着单支深入搜索到无法继续(所有合法移动都已经被走过了)时或者路径长度还没有达到预定值(8×8 棋盘为 63),那么就清除颜色标记,返回到上一层换一个分支继续深入搜索,可引入一个栈来记录路径,并实施返回上一层的回溯操作。
在 DFS 中,需要递归调用knightTour函数,不断将结点传入此函数,从而获取这个结点能够走的最长的 path。knightTour函数需要四个传递参量:
- n :当前树的深度
- path :这个结点前所有已访问的点的列表
- u :我们能够探索的点
- limit :搜索总深度限制
当knightTour被调用时,首先检查基础状态,如果 path 包含有 64 个结点,函数knightTour返回 True 表示已经找到一条可周游的路径;如果 path 还不够长,则选择一个新结点,并以此为参数调用自身。
DFS 对结点的追踪:DFS 算法还需要使用颜色来追踪图中哪些结点已经被访问过了。未访问的结点染为白色,访问过的染为灰色。如果当前结点的全部邻接结点都被访问且没有达到访问全部 64 个结点,就表示到了一条死路,这时需要进行回溯。回溯机制在knightTour返回 False 时启动(即递归的终止条件)。
DFS 使用栈:在 BFS 里用 Queue(队列)来跟踪要访问的结点,而在 DFS 里由于使用了递归,也即默认使用了 Stack(栈)来实现回溯机制。
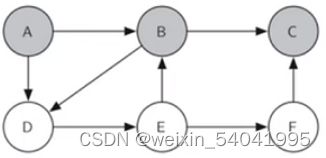
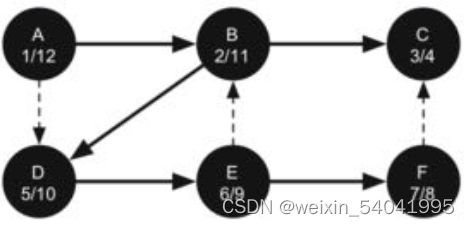
以下为一个骑士周游的问题的简单实例,该实例以图 4 的 A 顶点为起始点,将 A 染为灰色。从调用knightTour(0,path,A,6)开始,同时假设 Vertex 类中getConnections函数按字母顺序返回相邻顶点列表。
图4 从 A 开始
与 A 相邻的顶点是 B 和 D,在字母序上,B 在 D 之前,算法选择 B 来进行下一次探索,将 B 染成灰色,结果如图 5 所示。
图5 探索 B
与 B 相邻的顶点是 C 和 D,所以先探索 C 顶点,将 C 染成灰色,结果如图 6 所示。
图6 探索 C
顶点 C 没有相邻的白色顶点,走进了一条死胡同。这时,将 C 的颜色改为白色,然后从递归调用回溯到仍有可搜索子顶点的顶点,于是回到 B,结果如图 7 所示。
图7 回溯到 B
探索列表中的下一个顶点是顶点 D,将 D 染成灰色,结果如图 8 所示。
图8 探索 D
然后探索与 D 相邻的未被访问过的 E,将 E 染成灰色,结果如图 9 所示。
图9 探索 E
然后探索与 E 相邻的未被访问过的 F,将 F 染成灰色,结果如图 10 所示。
图10 探索 F
与 F 相邻的未被访问的只剩 C,然而,此时 n 小于 limit 的判断结果是假,所以可以知道已经遍历了图里的所有顶点,如图 11 所示。在算法中,此时将通过返回 True ,来表明已经成功地找到了这张图的一个周游方式,path 中的列表记录为 [A,B,D,E,F,C],这正是遍历这张图的顺序。
图11 探索完成
图 12 展示了一个 8×8 棋盘上的完整周游图。除此之外,还有很多种成功的可能。并且通过一些对函数的修饰,也能得到一个开始和中止于同一格子的周游路线。
图12 一个棋盘上完整的周游
编程要求
根据提示,在右侧编辑器中的 Begin-End 区间补充代码,完成genLegalMoves、knightGraph和knightTour方法,建立骑士周游图,最终解决骑士周游问题。Graph 和 Vertex 类的相关知识请参考图抽象数据类型的Python实现。
测试说明
平台会对你编写的代码进行测试,比对你输出的数值与实际正确的数值,只有所有数据全部计算正确才能通过测试:
测试输入:
5 4
输入说明:输入字符串以空格隔开,第一个数字为棋盘的边界大小,若为 5,则是一个 5×5 大小的棋盘;第二个数字表示骑士周游的起始顶点位置。
预期输出:
4701181102118925121922156314231613241720
输出说明:输出为骑士周游经过的格子位置序列,即对图进行深度优先遍历的顺序。
测试输入:
5 22
预期输出:
2215121981102118925162314361347011201724
提示:
d = []d.append((1,3))d.append((2,2))print(d)
输出:
[(1, 3), (2, 2)]
开始你的任务吧,祝你成功!
from graphs import Graph, Vertex
'''请在Begin-End之间补充代码, 完成genLegalMoves、knightGraph和knightTour函数'''
# 合法走棋位置函数
def genLegalMoves(x,y,bdSize):
# 存储八个合法走棋位置
newMoves = []
# 马走日8个格子的坐标偏移值
moveOffsets = [(-1,-2),(-1,2),(-2,-1),(-2,1),
( 1,-2),( 1,2),( 2,-1),( 2,1)]
for i in moveOffsets:
newX = x + i[0]
newY = y + i[1]
# 调用legalCoord方法判断newX和newY是否走出棋盘
# 只有落在棋盘里的才通过append加到newMoves里
# ********** Begin ********** #
if legalCoord(newX,bdSize) and legalCoord(newY,bdSize):
newMoves.append((newX,newY))
# ********** End ********** #
return newMoves
# 确认不会走出棋盘
def legalCoord(x,bdSize):
if x >= 0 and x < bdSize: # 不得超出正方形棋盘的边界
return True
else:
return False
# 构建走棋关系图
def knightGraph(bdSize):
# 建立空图ktGraph
ktGraph = Graph()
# 遍历每个格子
for row in range(bdSize):
for col in range(bdSize):
# 将每个格子都编号为nodeId
nodeId = posToNodeId(row,col,bdSize)
# 单步合法走棋
newPositions = genLegalMoves(row,col,bdSize)
# 对每个位置进行判断
for e in newPositions:
nid = posToNodeId(e[0],e[1],bdSize)
# 将顶点和形成的边加到图ktGraph中
# ********** Begin ********** #
ktGraph.addEdge(nodeId,nid)
# ********** End ********** #
return ktGraph
# 根据棋盘行、列确定索引值
def posToNodeId(row,col,bdSize):
return row*bdSize+col
def knightTour(n,path,u,limit):
# n:层次; path:路径; u:当前顶点; limit:搜索总深度
u.setColor('gray') # 当前顶点设为灰色,表示正在探索
path.append(u) # 当前顶点加入路径
if n < limit:
nbrList = list(u.getConnections()) # 对当前顶点连接的所有合法移动逐一深入
i = 0
done = False
while i < len(nbrList) and not done:
# 选择白色未经过的顶点深入
# 层次加1,递归调用knightTour深入
# ********** Begin ********** #
if nbrList[i].getColor() == 'white':
done = knightTour(n+1,path,nbrList[i],limit)
# ********** End ********** #
i = i + 1
# 都无法完成总深度,回溯,试本层下一个顶点
if not done:
path.pop()
u.setColor('white')
else:
done = True
return done第2关:骑士周游算法改进
任务描述
本关任务:编写代码实现骑士周游算法的改进,从而提高算法的性能。
相关知识
为了完成本关任务,你需要掌握: 1.骑士周游算法性能分析; 2.如何实现骑士周游算法改进。
骑士周游算法性能分析
当前实现的骑士周游算法是一个时间复杂度为 O(![]() ) 的算法,其中 N 是棋盘格的数目,k 是一个小的常数。因此,骑士周游问题的性能高度依赖于棋盘大小。例如:
) 的算法,其中 N 是棋盘格的数目,k 是一个小的常数。因此,骑士周游问题的性能高度依赖于棋盘大小。例如:
- 在 5×5 的棋盘上,一个相当快的电脑可以在 1.5 秒内找到一个周游路径;
- 在 8×8 的棋盘上,根据你电脑运行速度的不同,可能需要等半小时才能得到结果。
这是一个指数时间复杂度的算法,其搜索过程表现为一个层次为 N 的树。如图 1 所示,树的根结点代表搜索的起始点,从这一点开始,算法生成并检查了骑士每一个可能的移动位置。因此,骑士可移动位置的多少取决于骑士在棋盘中的位置。在角上,骑士只有两个合法的移动位置;在与角相邻的方格中,有三个合法的移动位置;在棋盘的中间则有八个。
图1 一个骑士周游问题的搜索树
图 2 展示了棋盘上每个方格中可能移动位置的个数。在树的第二层,对于我们正在探索的位置又有 2 到 8 个可能的移动位置。可能需要检查的位置数与搜索树的结点数一样多。
图2 棋盘上每个方格的可能移动数目
实现骑士周游算法改进
为了降低算法的时间复杂度,Warnsdorff 提出了 Warnsdorff 算法,对 nbrList 的灵巧构造,以特定方式排列顶点访问次序,可以使得 8×8 棋盘的周游路径搜索时间降低到秒级。
- 初始算法中的 nbrList,直接以原始顺序来确定深度优先搜索的分支次序;
- 新的算法仅修改遍历下一格的次序,当前顶点 u 的合法移动目标棋盘格排序为:具有最少合法移动目标的格子优先搜索。
首先去访问最少可能的格子会迫使骑士尽早的进入边角的格子,进而保证骑士尽早访问那些不容易到达的角落,并且在需要的时候,通过中间的方格跳跃着穿过棋盘。利用这种先验的知识来改进算法性能的做法,称作为“启发式规则”。
启发式搜索经常被用在人工智能领域,可以有效地减小搜索范围、更快达到目标等。如棋类程序算法,会预先存入棋谱、布阵口诀、高手习惯等“启发式规则”,能够在最短时间内,从海量的棋局落子点搜索树中,定位最佳落子。
编程要求
根据提示,在右侧编辑器中的 Begin-End 区间补充代码,完成orderByAvail和knightTourBetter方法,实现骑士周游问题的算法改进,保证每一次选择有最少可能移动位置的顶点进行探索。
测试说明
平台会对你编写的代码进行测试,比对你输出的数值与实际正确的数值,只有所有数据全部计算正确才能通过测试:
测试输入:
8 4
输入说明:输入字符串以空格隔开,第一个数字为棋盘的边界大小,若为 8,则是一个 8×8 大小的棋盘;第二个数字表示骑士周游的起始顶点位置。
预期输出:
4143146635347625258483316111515216233855615157405056412493137223954604530362620374328188212293525193444594932422717010
输出说明:输出为骑士周游经过的格子位置序列,即对图进行深度优先遍历的顺序。
提示:
d = []d.append((3,6))d.append((4,2))d.append((2,5))print(d)d.sort(key=lambda x: x[0]) # 以元素的第一项来进行从小到大排序print(d)
输出:
[(3, 6), (4, 2), (2, 5)][(2, 5), (3, 6), (4, 2)]
开始你的任务吧,祝你成功!
from graphs import Graph, Vertex
'''请在Begin-End之间补充代码, 完成orderByAvail和knightTourBetter函数'''
# 合法走棋位置函数
def genLegalMoves(x,y,bdSize):
newMoves = []
moveOffsets = [(-1,-2),(-1,2),(-2,-1),(-2,1),
( 1,-2),( 1,2),( 2,-1),( 2,1)]
for i in moveOffsets:
newX = x + i[0]
newY = y + i[1]
if legalCoord(newX,bdSize) and legalCoord(newY,bdSize):
newMoves.append((newX,newY))
return newMoves
# 确认不会走出棋盘
def legalCoord(x,bdSize):
if x >= 0 and x < bdSize:
return True
else:
return False
# 构建走棋关系图
def knightGraph(bdSize):
ktGraph = Graph()
for row in range(bdSize):
for col in range(bdSize):
nodeId = posToNodeId(row,col,bdSize)
newPositions = genLegalMoves(row,col,bdSize)
for e in newPositions:
nid = posToNodeId(e[0],e[1],bdSize)
ktGraph.addEdge(nodeId,nid)
return ktGraph
# 根据棋盘行、列确定索引值
def posToNodeId(row,col,bdSize):
return row*bdSize+col
def orderByAvail(n):
resList = []
for v in n.getConnections():
if v.getColor() == 'white':
c = 0
for w in v.getConnections():
# 若w未被搜索过,颜色是白色,则c的值加1
# ********** Begin ********** #
if w.getColor() == 'white':
c = c + 1
# ********** End ********** #
resList.append((c,v))
# 对有合法移动目标格子数量的顶点进行从小到大排序
# ********** Begin ********** #
resList.sort(key=lambda x: x[0])
# ********** End ********** #
return [y[1] for y in resList]
def knightTourBetter(n,path,u,limit): #use order by available function
u.setColor('gray')
path.append(u)
if n < limit:
# 调用orderByAvail函数,将当前结点的有序合法移动位置存入nbrList
# ********** Begin ********** #
nbrList = orderByAvail(u)
# ********** End ********** #
i = 0
done = False
while i < len(nbrList) and not done:
# 选择白色未经过的顶点深入
# 层次加1,递归调用knightTourBetter深入
# ********** Begin ********** #
if nbrList[i].getColor() == 'white':
done = knightTourBetter(n+1,path,nbrList[i],limit)
# ********** End ********** #
i = i + 1
if not done: # prepare to backtrack
path.pop()
u.setColor('white')
else:
done = True
return done
第3关:通用深度优先搜索
任务描述
本关任务:编写代码基于 Python 语言,实现通用深度优先搜索。
相关知识
为了完成本关任务,你需要掌握: 1.什么是通用深度优先搜索; 2.如何实现通用深度优先搜索。
通用深度优先搜索
骑士周游问题是深度优先搜索中的一个特殊案例,它是以创建深度最深并无分支的优先搜索树为目标。事实上,更一般的深度优先搜索更容易实现。它的目标是尽可能深地搜索,连接图中尽可能多的顶点以及仅在必要时建立分支。有时候深度优先搜索会创建多棵树,称之为深度优先森林。
与广度优先搜索相同,深度优先搜索也使用前驱链接来创建树。此外,深度优先搜索会使用两个附加的 Vertex 类的实例变量。这两个新的实例变量是:
- 发现时间:记录某个顶点第一次出现前算法的操作步数;
- 完成时间:是某个顶点被标记为黑色之前算法的操作步数。
即需要对 Vertex 类进行扩展完善,在该类中加入这两个新的实例变量,并且这两种实例变量都有相应的设置以及取值的方法,如setDiscovery、setFinish、getDiscovery、getFinish方法,代码示例如下:
class Vertex:def __init__(self,num):……self.disc = 0 # 发现时间self.fin = 0 # 完成时间def setDiscovery(self,dtime): # 设置发现时间self.disc = dtimedef setFinish(self,ftime): # 设置完成时间self.fin = ftimedef getDiscovery(self): # 获取发现时间return self.discdef getFinish(self): # 获取完成时间return self.fin……
实现通用深度优先搜索
为了实现通用的深度优先搜索,需要创建一个继承于 Graph 类的方法类 DFSGraph。在该类中添加了一个时间实例变量,同时定义了dfs和dfsvisit两个方法来拓展图类。
dfs()方法 该方法用于对图中的白色顶点进行迭代,调用dfsvisit方法来遍历图中所有的顶点。在这过程中,将遍历所有顶点,而不是简单地从某个选定起始顶点开始搜索。这是为了保证图中所有顶点都被考虑到,并且没有顶点在深度优先森林中被遗漏。
dfsvisit(startVertex)方法 该方法作为辅助方法,辅助dfs实现图中所有顶点的访问。dfsvisit方法以一个叫做 startVertex 的单一顶点开始并尽可能深地探索所有相邻白色顶点。相比于广度优先搜索算法,dfsvisit方法除了内部循环的最后一行与bfs几乎相同。dfsvisit递归调用自身,以继续对更深层次的顶点进行探索,而bfs通过将顶点添加到一个队列中以便后续探索。
以下实例说明了深度优先搜索算法对一个较小的图的操作。搜索从图 1 中的 A 顶点开始。由于所有的顶点在开始时都是白色的,所以算法首先访问 A 顶点,然后将其颜色设置为灰色,以表明这个顶点已被探索过,并且将“发现时间”设置为 1。由于 A 顶点拥有两个相邻顶点(B 和 D),并且这两个顶点都需要被访问,所以可以任意地选择顶点访问。比如可以按照字母表顺序依次访问相邻顶点。
图1 访问 A
接下来访问 B 顶点,然后将其颜色设置为灰色,并且将“发现时间”设置为 2,结果如图 2 所示。
图2 访问 B
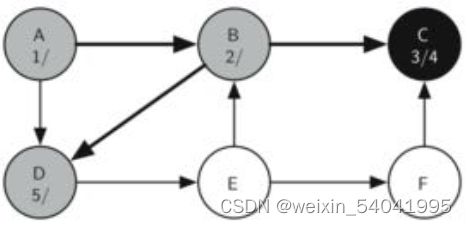
由于 B 顶点同样有两个相邻顶点(C 和 D),所以按照字母表顺序接着访问 C 顶点,结果如图 3 所示。
图3 访问 C
在访问 C 顶点的过程中,到达了树的一枝的末端。在将 C 顶点涂为灰色并将“发现时间”设置为 3 后,算法认为 C 顶点没有相邻顶点。这意味着已经完成了对 C 顶点搜索,并且可以将其涂为黑色并设置“完成时间”为 4,结果如图 4 所示。
图4 已完成对 C 顶点搜索
由于 C 顶点在一枝的末端,所以返回到 B 顶点并继续探索 B 顶点的相邻顶点。由于 B 顶点未访问的相邻顶点仅有 D,所以访问 D 顶点并从此继续搜索,结果如图 5 所示。
图5 访问 D
接下来访问与 D 相邻的 E 顶点,结果如图 6 所示。
图6 访问 E
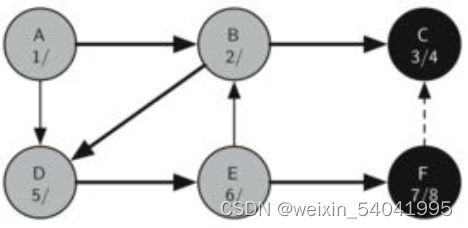
E 顶点有 B 和 F 两个相邻顶点。通常是按照字母表顺序探索这些相邻顶点,但由于 B 顶点已经被标记为灰色,算法识别出不应该访问会导致算法陷入死循环的 B 顶点。所以继续探索列表中的下一个顶点 F,结果如图 7 所示。
图7 访问 F
F 顶点只有一个相邻顶点 C,但由于 C 顶点已经被标记为黑色,不能继续探索,并且算法也到达了树的另一枝的末端。从此开始,算法将一路运算返回初始顶点,设置“完成时间”并设置顶点颜色为黑色,如图 8-12 所示。
图8 设置顶点 F 为黑色
图9 设置顶点 E 为黑色
图10 设置顶点 D 为黑色
图11 设置顶点 B 为黑色
图12 设置顶点 A 为黑色
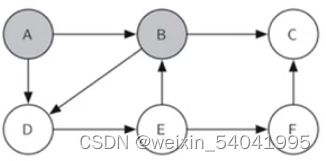
顶点的“发现时间”和“完成时间”具有类似括号的性质。这个性质意味着深度优先树中一个特定顶点的所有的子顶点拥有与它们的父顶点相比更晚的“发现时间”和更早的“ 完成时间”。图 12 展示了深度优先搜索算法建立的树,其中实线表示被添加到深度优先搜索树中的边,即对顶点进行探索时经过的边。
编程要求
根据提示,在右侧编辑器中的 Begin-End 区间补充代码,完成 DFSGraph 类,补充完善dfs和dfsvisit方法,实现对图的通用深度优先搜索遍历。
测试说明
平台会对你编写的代码进行测试,比对你输出的数值与实际正确的数值,只有所有数据全部计算正确才能通过测试:
测试输入:
5,0 1,0 3,1 2,1 3,2 4,3 2,3 4
输入说明:输入字符串用于创建深度优先搜索遍历的初始图,其中第一个逗号前的数值表示所创建的图的顶点数,剩下的部分同样以逗号进行分隔。分隔成的每一小段又以空格分隔成两部分,分别表示所添加边的第一个顶点和第二个顶点。
预期输出:
01243
输出说明:输出为对图进行深度优先搜索遍历的顺序,当遇到多个相邻顶点时,按照从小到大的顺序依次访问相邻顶点。
测试输入:
7,0 1,0 2,0 3,1 2,1 4,2 4,2 5,3 5,4 6,5 4,5 6
预期输出:
0124653
提示:
class A:def climbStairs(self, n):if n == 1:return 1elif n == 2:return 2else:return self.climbStairs(n - 1) + self.climbStairs(n - 2) # self替换成类的实例Fn = A()print(Fn.climbStairs(3))
输出:
3
开始你的任务吧,祝你成功!
from graphs import Graph
'''请在Begin-End之间补充代码, 完成DFSGraph中的dfs和dfsvisit函数'''
class DFSGraph(Graph):
def __init__(self):
super().__init__()
self.time = 0 # 时间实例变量
self.resList = [] # 存储遍历序列
def dfs(self):
for aVertex in self:
aVertex.setColor('white')
aVertex.setPred(-1)
for aVertex in self:
# 如果顶点的颜色为白色'white',调用dfsvisit函数探索顶点
# ********** Begin ********** #
if aVertex.getColor() == 'white':
self.dfsvisit(aVertex)
# ********** End ********** #
def dfsvisit(self,startVertex):
startVertex.setColor('gray')
self.resList.append(startVertex)
self.time += 1
startVertex.setDiscovery(self.time)
for nextVertex in startVertex.getConnections():
# 如果顶点nextVertex的颜色为白色'white',则表示未被探索
# 设置其前驱为startVertex
# 递归调用dfsvisit函数进行更深层次的探索
# ********** Begin ********** #
if nextVertex.getColor() == 'white':
nextVertex.setPred(startVertex)
self.dfsvisit(nextVertex)
# ********** End ********** #
startVertex.setColor('black')
self.time += 1
startVertex.setFinish(self.time)