冒泡排序算法的Python实现(头歌实践教学平台)
第1关:冒泡排序的实现
任务描述
本关任务:编写代码实现冒泡排序。
相关知识
为了完成本关任务,你需要掌握: 1.如何实现冒泡排序; 2.冒泡排序的算法分析。
冒泡排序
冒泡排序又称起泡排序,它的算法思路在于对无序表进行多趟比较交换,每趟都包括了多次两两相邻数据项的比较,并将逆序的数据项互换位置,最终能将本趟的最大项就位。如果列表有 n 个数据项,经过 n-1 趟比较交换就能实现对整个数据表的排序。由于每趟的过程类似于“气泡”在水中不断上浮到水面的经过,因此称之为“冒泡排序”。在冒泡排序中,每趟排序所需要的比较次数是不同的,如以下所述:
-
第 1 趟比较交换时,共有 n-1 对相邻数据进行比较,一旦经过最大项,则最大项会一路交换到达最后一项;
-
第 2 趟比较交换时,由于最大项已经就位,需要排序的数据减少为 n-1 个,则共有 n-2 对相邻数据进行比较;
-
直到第 n-1 趟完成后,最小项一定在列表首位,就无需再执行其他步骤,排序结束。
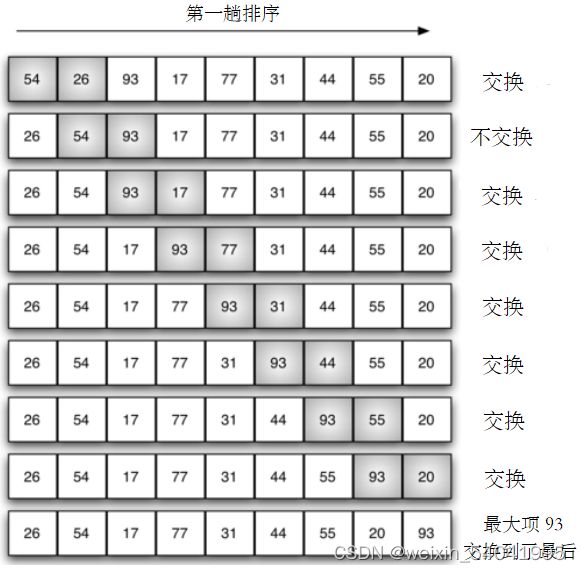
以下图 1 展示了冒泡排序的第 1 趟排序过程。为了进行从小到大的排序,在两两比较的过程中,只要前者大于后者,就交换位置。
图1 冒泡排序的第 1 趟排序
对于图 1 中具有 9 个数据项的列表,第 1 趟排序总共需要比较 8 次,排序具体过程为:
-
将第一个数据项 54 和相邻的 26 进行比较,54 大于 26,交换位置;
-
再将 54 与 93 进行比较,54 小于 93,不必交换;
-
再将 93 与 17 进行比较,93 大于 17,交换位置;
-
再将 93 与 77 进行比较,93 大于 77,交换位置;
-
再将 93 与 31 进行比较,93 大于 31,交换位置;
-
再将 93 与 44 进行比较,93 大于 44,交换位置;
-
再将 93 与 55 进行比较,93 大于 55,交换位置;
-
再将 93 与 20 进行比较,93 大于 20,交换位置。
此时第 1 趟排序结束,列表中的最大项 93 确定了最终位置,交换到了列表的最后。第 1 趟排序并未使整个列表有序,还需继续进行其他趟的排序。
冒泡排序的算法分析
无序表初始数据项的排列状况对冒泡排序没有影响,算法过程总需要 n-1 趟,随着趟数的增加,比较次数逐步从 n-1 减少到 1,并包括可能发生的数据项交换。所以对于整个冒泡排序过程,其比较次数是 1~n-1 的累加,故比较的时间复杂度是O(。![]() )
)
在冒泡排序中,每一次比较都可能发生交换,通常每次交换包括 3 次赋值。交换列表中的两项需要一个附加的储存空间来作为暂存位置。以下代码可以对列表 list 中的第 i 项和第 j 项进行交换,有了暂存位置 temp,其中一个值就不会被覆盖。
temp = list[i]list[i] = list[j]list[j] = temp
关于交换次数,时间复杂度也是O(。![]() )
)
-
最好的情况是列表在排序前已经有序,交换次数为 0;
-
最差的情况是每次比较都要进行交换,交换次数等于比较次数;
-
平均情况则是最差情况的一半。
冒泡排序通常作为时间效率较差的排序算法,是其它算法的对比基准。其效率主要差在每个数据项在找到其最终位置之前都必须要经过多次比对和交换,其中大部分的操作是无效的。但它的优势是无需任何额外的存储空间开销。
编程要求
在右侧编辑器中的 Begin-End 区间补充代码,根据冒泡排序的算法思想完成bubbleSort方法,从而实现对无序表的排序。
测试说明
平台会对你编写的代码进行测试,比对你输出的数值与实际正确的数值,只有所有数据全部计算正确才能通过测试:
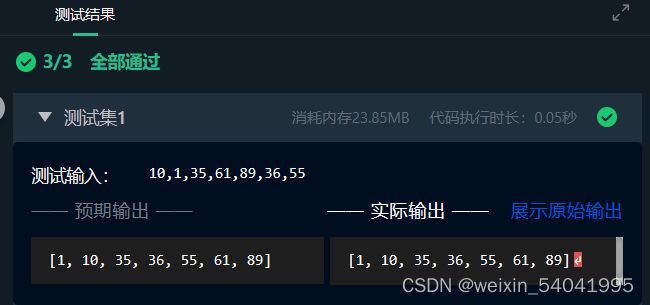
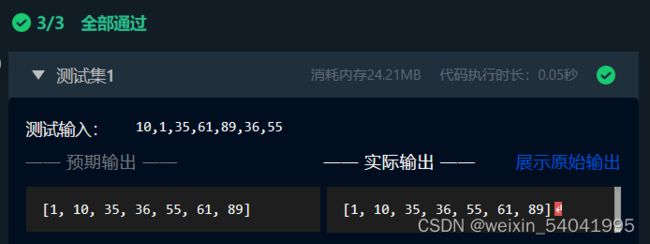
测试输入:
10,1,35,61,89,36,55
输入说明:输入为需要对其进行排序的无序表
预期输出:
[1, 10, 35, 36, 55, 61, 89]
输出说明:输出的是对无序表进行冒泡排序后的结果,以列表的形式展现
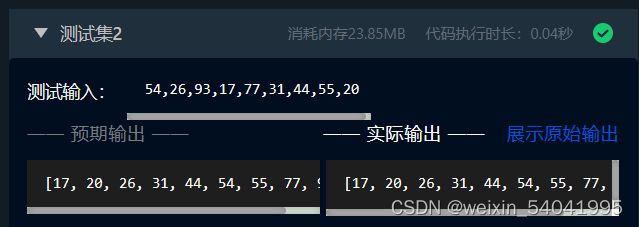
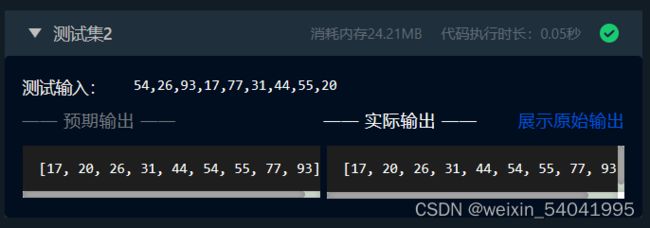
测试输入:
54,26,93,17,77,31,44,55,20
预期输出:
[17, 20, 26, 31, 44, 54, 55, 77, 93]
开始你的任务吧,祝你成功!
'''请在Begin-End之间补充代码, 完成bubbleSort函数'''
def bubbleSort(alist):
for passnum in range(len(alist)-1,0,-1): # passnum从n-1开始,一直减到1,总共进行n-1趟排序
for i in range(passnum): # i从0开始,一直到(passnum-1),包括了这一趟比较的范围
# 对第i项和相邻的第i+1进行比较
# 如果是逆序的,就交换
# ********** Begin ********** #
if alist[i]>alist[i+1]:
temp=alist[i]
alist[i]=alist[i+1]
alist[i+1]=temp
# ********** End ********** #第2关:冒泡排序算法的改进
任务描述
本关任务:编写代码实现改进的冒泡排序。
相关知识
为了完成本关任务,你需要掌握如何改进冒泡排序算法。
由于冒泡排序必须要在最终位置找到之前不断交换数据项,其中大部分的操作是无效的,这些无效的交换操作会消耗许多时间,所以它经常被认为是最低效的排序方法。
但是,由于冒泡排序要遍历整个未排好的部分,它可以做一些大多数排序方法做不到的事。尤其是如果在某趟排序的过程中没有发生交换,就可以断定列表已经排好。因此可以对冒泡排序进行改良,使其在已知列表排好的情况下提前结束。也就是说,如果一个列表只需要几趟排序就可排好,冒泡排序就占有很大的优势,它可以在发现列表已排好时立刻结束。这种改进版的冒泡排序算法被称为“短路冒泡排序”。
下面是一个冒泡排序的示例,图 1 展示了第 1 趟排序的过程。
图1 第 1 趟排序
由于这是一个具有 7 个数据项的列表,因此第 1 趟排序需要进行 6 次相邻数据项的比较,其具体过程描述为:
-
将第一个数据项 10 和相邻的 1 进行比较,10 大于 1,交换位置;
-
再将 10 与 35 进行比较,10 小于 35,不必交换;
-
再将 35 与 61 进行比较,35 小于 61,不必交换;
-
再将 61 与 89 进行比较,61 小于 89,不必交换;
-
再将 89 与 36 进行比较,89 大于 36,交换位置;
-
再将 89 与 55 进行比较,89 大于 55,交换位置。
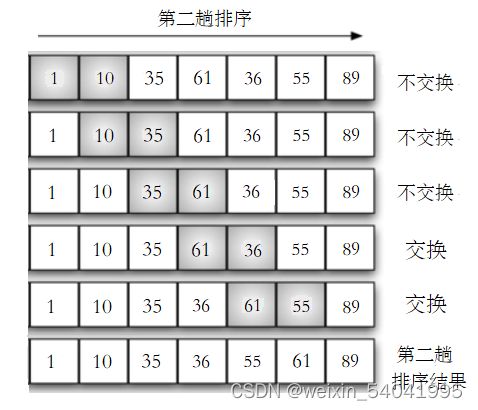
此时第 1 趟排序结束后,列表中的最大项 89 确定了最终位置,交换到了列表的最后。由于这一趟排序的过程发生了交换,就继续下一趟的排序,图 2 展示了第 2 趟排序的过程。
图2 第 2 趟排序
由于第 1 趟排序确定了一个最大项 89,将其放在了列表最后,因此第 2 趟排序只需进行 5 次两两比较,其具体过程描述为:
-
将第一个数据项 1 和相邻的 10 进行比较,1 小于 10,不用交换位置;
-
再将 10 与 35 进行比较,10 小于 35,不必交换;
-
再将 35 与 61 进行比较,35 小于 61,不必交换;
-
再将 61 与 36 进行比较,61 大于 36,交换位置;
-
再将 61 与 55 进行比较,61 大于 55,交换位置。
此时第 2 趟排序结束后,列表中除 89 之外的最大项 61 确定了最终位置。由于这一趟排序的过程发生了交换,就继续下一趟的排序,图 3 展示了第 3 趟排序的过程。
图3 第 3 趟排序
第 3 趟排序的四次比较都未发生交换,说明此时列表已经有序,排序结束。
该改进算法的代码实现是通过增加一个 exchanges 变量来完成,该变量用来监测每趟比较是否发生过交换。当进行相邻数据项的两两比较时,若发生了交换,就设置 exchanges 为 True。若某一趟排序结束后,exchanges 都未被设置为 True,说明已经排好序,可以提前结束算法。
编程要求
在右侧编辑器中的 Begin-End 区间补充代码,完成shortbubbleSort方法,在上一关冒泡排序算法的基础上,通过添加变量 exchanges 来监测每趟比较是否发生过交换,从而实现对冒泡排序的改进。
测试说明
平台会对你编写的代码进行测试,比对你输出的数值与实际正确的数值,只有所有数据全部计算正确才能通过测试:
测试输入:
10,1,35,61,89,36,55
输入说明:输入为需要对其进行排序的无序表。
预期输出:
[1, 10, 35, 36, 55, 61, 89]
输出说明:输出的是对无序表进行排序后的结果,以列表的形式展现。
测试输入:
54,26,93,17,77,31,44,55,20
预期输出:
[17, 20, 26, 31, 44, 54, 55, 77, 93]
'''请在Begin-End之间补充代码, 完成shortbubbleSort函数'''
def shortbubbleSort(alist):
exchanges = True # 通过exchanges监测每趟比对是否发生过交换
passnum = len(alist)-1 # passnum从n-1开始
# 当还未完成n-1趟排序 且 上一趟排序发生了交换,则继续下一趟排序
while passnum > 0 and exchanges:
# 每趟排序首先将exchanges置为False,只要发生了交换就将其置为True
# ********** Begin ********** #
exchanges=False
for i in range(len(alist)-1):
if alist[i]>alist[i+1]:
temp=alist[i]
alist[i]=alist[i+1]
alist[i+1]=temp
exchanges=True
# ********** End ********** #