人工智能学习5(特征抽取)

编译环境：PyCharm

特征抽取

特征选择和特征抽取都减少了数据的维度(降维)，但是特征选择是得到原有特征的子集，特征抽取是将原有特征结果函数映射转化为新的特征。
特征抽取分为无监督特征抽取和有监督特征抽取。

无监督特征抽取(之PCA)

无监督：没有标签
PCA降维(主成分分析)基本思想：构造一系列原始特征的线性组合形成的线性无关低维特征，以去除数据的相关性，并使降维后的数据最大程度保持原始高维数据的方差信息。
去中心化处理：x-x的平均值
去中心化后，样本均值在0
均值：描述样本集合的中心点
标准差：各个样本到均值处的平均距离
标准差可以用来描述数据的散布程度
方差：标准差的平方
标准差和方差只能描述一维数据
协方差是两个变量之间的线性相关程度的度量(协方差为0表示两个变量没有相关性，为正数则正相关)
协方差矩阵可以用来描述多维数据的线性相关性。

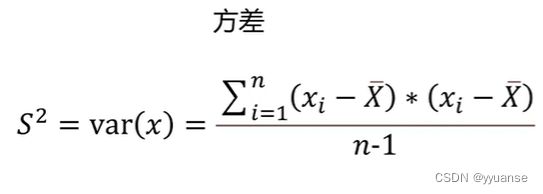
cov(x,y)=cov(y,x)
var(x)=cov(x,x)

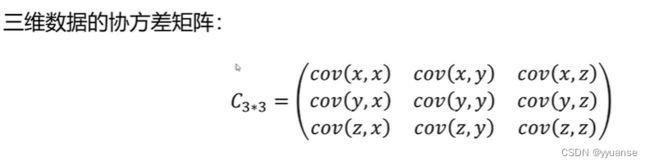
可以看出协方差矩阵是对称的，对角线为方差。

同一个向量在不同基底的变换，选择不同的及可以对同样一组数据给出不同的表示。

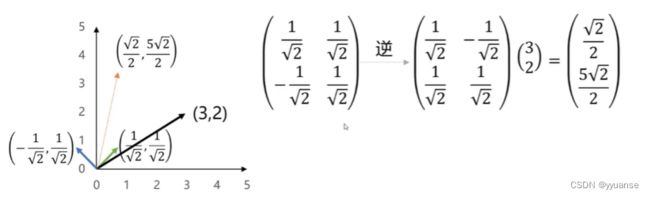
要尽可能保留原有信息，要求投影后的值尽可能分散，不重合。

代码实现鸢尾花数据集无监督特征抽取

在sklearn中的datasets中，已经内置了鸢尾花的数据集，直接使用即可

from sklearn import datasets
iris = datasets.load_iris()
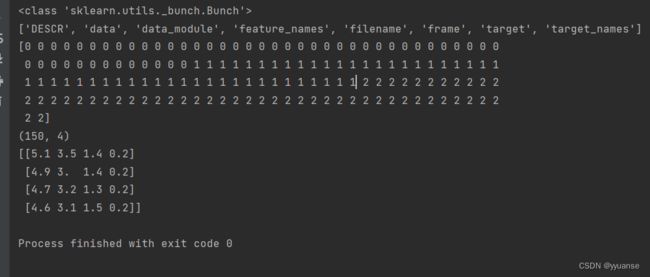
print(type(iris))
# 查看属性有哪些
print(dir(iris))
# 打印标签
print(iris.target)
# 获取样本和标签
X=iris.data
print(X.shape)
# 打印前四行
print(X[:4])

对应的打印结果：

可以看到返回的是一个类。Bunch，用于描述数据集。其属性DESCR是数据描述，target_names是标签名，可自定义默认为文件夹名字，filenames文件夹名，target文件分类可以看成y值，data是数据数组可以看成X。
对数据进行主成分分析

print("------主成分分析PCA-------")
from sklearn.decomposition import PCA
# 实例化
pca=PCA()
X_pca = pca.fit_transform(X)
# 查看X_pca的前四行数据，只看小数点后两位
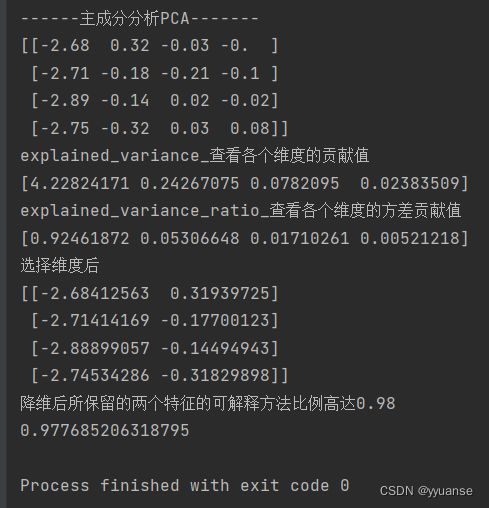
print(np.round(X_pca[:4], 2))
# 由于没有设置维度，上面只会处理的数据但是没有实现降维
# 通过 explained_variance_ 可以查看各个维度的贡献值
print("explained_variance_查看各个维度的贡献值")
print(pca.explained_variance_)
# 通过 explained_variance_ratio_ 查看各个维度的方差贡献值
print("explained_variance_ratio_查看各个维度的方差贡献值")
print(pca.explained_variance_ratio_)
# 从上面的结果，可以看到保留两个维度，前两个维度较为合理，前两个维度的重要性远高于另外两个
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
print("选择维度后")
print(X_pca[:4])
print("降维后所保留的两个特征的可解释方法比例高达0.98")
print(pca.explained_variance_ratio_.sum())

有监督特征抽取(之LDA)

LDA(线性判别分析法)
LDA思想：投影后类内方差最小，类间方差最大
和PCA一样通过投影的方法达到去除数据间冗余的一种算法。既可以作为降维的方法，也可以作为分类的方法。
PCA会忽略给出的标签，LDA会利用到这些标签。
LDA降维最多可以降到类别数的k-1的维度，PCA没有这个限制
LDA不适合对非高斯分布的样本进行降维
LDA有时会产生过拟合的问题

在人脸识别等图像识别领域广泛应用。

线性分类器(速度快)：“超平面”将两个样本隔离开
常见线性分类器：LR逻辑回归、贝叶斯分类、线性回归、SVM（线性核）
非线性分类(拟合能力更强)：曲面或者多个“超平面”
常见非线性分类器：决策树、GBDT、多层感知机、SVM（高斯核）

代码实现,生成自己的数据集并进行有监督特征抽取(LDA)

生成自己的数据集

# 生成自己的数据集
from sklearn.datasets import make_classification
X,y=make_classification(
    n_samples=1000, # 产生1000个样本
    n_features=4,   # 每个样本有4个列
    n_repeated=0,
    n_classes=3,    # 一共三个标签(3个类别)
    n_clusters_per_class=1,
    class_sep=0.5,
    random_state=10 # 随机值设置为10
)
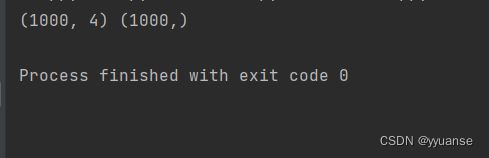
print(X.shape,y.shape)

PCA降维和LDA降维对比

# PCA降维
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
pca = PCA(n_components=2) # 设置目标维度为2
X_pca = pca.fit_transform(X)
# 绘制图
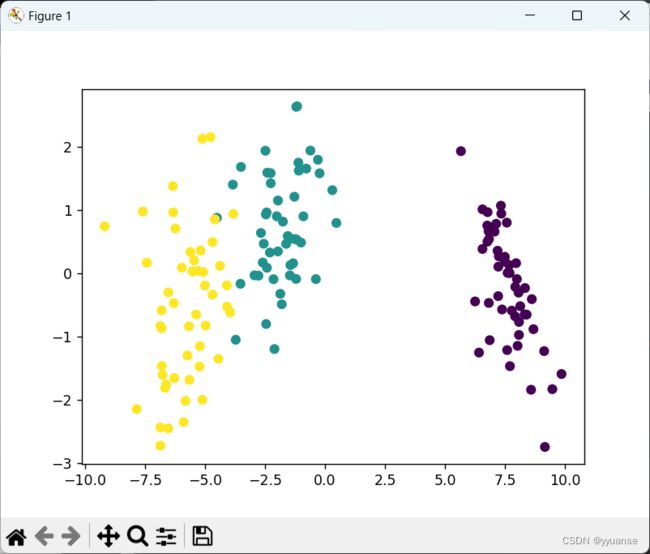
plt.scatter(X_pca[:,0],X_pca[:,1],c=y)
plt.show()


# 使用LDA降维
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 实例化
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit_transform(X,y)  # LDA是需要数据以及标签的
plt.scatter(X_lda[:,0],X_lda[:,1],c=y)
plt.show()

代码实现LDA降维对鸢尾花数据进行特征抽取

# 使用LDA对鸢尾花数据进行降维
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
iris = datasets.load_iris()
X_iris,y_iris = iris.data,iris.target
# 实例化LDA
lda = LinearDiscriminantAnalysis(n_components=2)
X_iris_lda = lda.fit_transform(X_iris,y_iris)
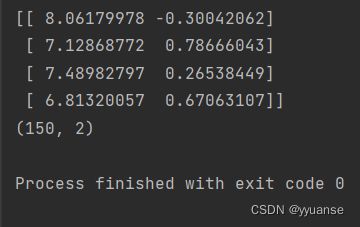
print(X_iris_lda[:4])
print(X_iris_lda.shape)
plt.scatter(X_iris_lda[:,0],X_iris_lda[:,1],c=y_iris)
plt.show()