力扣-数组-统计数组中的元素
力扣-数组-统计数组中的元素
- 645 错误的集合
- 697 数组的度
- 448 找到所有数组中消失的数字
- 41 缺失的第一个正数
- 442 数组中重复的数据
- 274 H 指数
用异或来交换两个变量是错误的。今天看到了一首诗:
《linux多线程服务端编程》501页分析了,
用异或运算交换变量,
是错误的行为。
并且不能加快运算,
也不能节省内存。
645 错误的集合
645 错误的集合
集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合 丢失了一个数字 并且 有一个数字重复 。
给定一个数组 nums 代表了集合 S 发生错误后的结果。
请你找出重复出现的整数,再找到丢失的整数,将它们以数组的形式返回。
示例 1:
输入:nums = [1,2,2,4]
输出:[2,3]
示例 2:
输入:nums = [1,1]
输出:[1,2]
提示:
2 <= nums.length <= 104
1 <= nums[i] <= 104
- 十分暴力:丢掉的那个数值 = 重复的+(正确和-错误和)
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
sort(nums.begin(), nums.end());
int n = nums.size();
int repeat;
for (int i = 0; i < n - 1; ++i) {
if (nums[i] == nums[i + 1])
repeat = nums[i];
}
int sum = 0, c_sum = (1 + n) * n / 2, loss;
for (int i = 0; i < n; ++i) sum += nums[i];
loss = repeat + c_sum - sum;
return {repeat, loss};
}
};
- 哈希表
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
vector<int> vec(2, 0); //存放最后结果
map<int, int> map1; //存放出现次数
for (int i = 1; i <= nums.size(); ++i) {
map1[i] += 1; //1到n之间的数先初始化为1
map1[nums[i - 1]] += 1; //累加nums中出现的次数
}
for (int i = 1; i<= nums.size(); i++) {
if(map1[i] == 3) vec[0] = i; //重复的数 次数为3
else if (map1[i] == 1) vec[1] = i; //缺失的数 次数为1
}
return vec;
}
};
- 官方给的七种方法。暴力的比我还暴力,复杂的也是够复杂
697 数组的度
697 数组的度
给定一个非空且只包含非负数的整数数组 nums,数组的度的定义是指数组里任一元素出现频数的最大值。
你的任务是在 nums 中找到与 nums 拥有相同大小的度的最短连续子数组,返回其长度。
示例 1:
输入:[1, 2, 2, 3, 1]
输出:2
解释:
输入数组的度是2,因为元素1和2的出现频数最大,均为2.
连续子数组里面拥有相同度的有如下所示:
[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]
最短连续子数组[2, 2]的长度为2,所以返回2.
示例 2:
输入:[1,2,2,3,1,4,2]
输出:6
提示:
nums.length 在1到 50,000 区间范围内。
nums[i] 是一个在 0 到 49,999 范围内的整数。
哈希表:用 字典(哈希表)计数,字典的 key 是元素,value 是该元素出现的次数。因此,字典中所有 value 的最大值就是数组的度 degree。
class Solution {
public:
int findShortestSubArray(vector<int>& nums) {
/*left 保存每个元素在数组中第一次出现的位置
right 保存每个元素在数组中最后一次出现的位置
counter 保存每个元素出现的次数*/
unordered_map<int, int> left, right, counter;
/*数组的度degree等于counter.values()的最大值*/
int degree = 0;
for (int i = 0; i < nums.size(); ++i) {
if(!left.count(nums[i])) left[nums[i]] = i; //第一次出现
right[nums[i]] = i;
counter[nums[i]] ++;
degree = max(degree, counter[nums[i]]);
}
/*对counter遍历*/
int result = nums.size();
for(auto& kv : counter) { //kv读取counter中的元素
/*代码段中的first或second用法:
map中的每个元素都对应一组键值对(pair)
键值对中的第一个成员称为first,第二个成员称为second
counter的first是元素,secend是次数*/
if(kv.second == degree) result = min(result, right[kv.first] - left[kv.first] + 1);
}
return result;
}
};
- 时间复杂度:O(N),因为对数组遍历了一遍,对counter 遍历了两遍。
- 空间复杂度:O(N),因为 counter 在最坏情况下会跟 nums 的元素个数相等。
Map+滑动窗口也可:先用map统计数字的个数和最大频数,再次遍历整个数组,用滑动窗口限制,找到最短的满足条件的窗口长度
448 找到所有数组中消失的数字
448 找到所有数组中消失的数字
给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组,数组中的元素一些出现了两次,另一些只出现一次。
找到所有在 [1, n] 范围之间没有出现在数组中的数字。
您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。
示例:
输入:
[4,3,2,7,8,2,3,1]
输出:
[5,6]
- 暴力
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> ans;
if(nums.empty() == 1) return ans;
vector<int> count(nums.size() + 1, 0);
for (int i = 0; i < nums.size(); ++i) count[nums[i]]++;
for (int i = 1; i <= nums.size(); ++i) {
if(count[i] == 0) ans.push_back(i);
}
return ans;
}
};
- 官方题解:标记数组
由于数字范围均在 [1,n] 中,我们也可以用一个长度为 n 的数组来代替哈希表。
注意到 nums 的长度恰好也为 n,能否让 nums 充当哈希表呢?
由于 nums 的数字范围均在 [1,n] 中,我们可以利用这一范围之外的数字,来表达是否存在的含义。
具体来说,遍历 nums,每遇到一个数 x,就让 nums[x−1] 增加 n。由于 nums 中所有数均在 [1,n] 中,增加以后,这些数必然大于 n。最后我们遍历 nums,若 nums[i] 未大于 n,就说明没有遇到过数 i+1。这样我们就找到了缺失的数字。
注意,当我们遍历到某个位置时,其中的数可能已经被增加过,因此需要对 n 取模来还原出它本来的值。
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
int n = nums.size();
for (auto& num: nums) {
int x = (num - 1) % n;
nums[x] += n;
}
vector<int> ret;
for (int i = 0; i < n; ++i) {
if (nums[i] <= n) ret.push_back(i + 1);
}
return ret;
}
};
- 时间复杂度:O(n)。其中 n 是数组 nums 的长度。
- 空间复杂度:O(1)。返回值不计入空间复杂度。
41 缺失的第一个正数
41 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
进阶:你可以实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案吗?
示例 1:
输入:nums = [1,2,0]
输出:3
示例 2:
输入:nums = [3,4,-1,1]
输出:2
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
提示:
0 <= nums.length <= 300
-231 <= nums[i] <= 231 - 1
原地hash: 将数组视为哈希表
只能使用常数级别的空间
class Solution {
public:
int firstMissingPositive(vector<int> &nums) {
for (int i = 0; i < nums.size(); i++) {
while (nums[i] > 0 && nums[i] <= nums.size() && nums[nums[i] - 1] != nums[i]) {
/*原本 i 位置的 nums[i] 已经交换到了别的地方
交换后到这里的新值不一定是适合这个位置的
因此需要重新进行判断交换,不能用if*/
int temp = nums[nums[i] - 1];
nums[nums[i] - 1] = nums[i];
nums[i] = temp;
//while (nums[i] != i + 1) {
// if (nums[i] <= 0 || nums[i] > nums.size() || nums[i] == nums[nums[i] - 1])
// break;
// int idx = nums[i] - 1;
// nums[i] = nums[idx];
// nums[idx] = idx + 1;
}
}
for (int i = 0; i < nums.size(); i++) {
if (nums[i] != (i + 1)) { //第一个“值不配位”
return (i + 1);
}
}
return (nums.size() + 1); //每个位置都正确
}
};
442 数组中重复的数据
442 数组中重复的数据
给定一个整数数组 a,其中1 ≤ a[i] ≤ n (n为数组长度), 其中有些元素出现两次而其他元素出现一次。
找到所有出现两次的元素。
你可以不用到任何额外空间并在O(n)时间复杂度内解决这个问题吗?
示例:
输入:
[4,3,2,7,8,2,3,1]
输出:
[2,3]
抄448只改一个数
class Solution {
public:
vector<int> findDuplicates(vector<int>& nums) {
vector<int> ans;
if(nums.empty() == 1) return ans;
vector<int> count(nums.size() + 1, 0);
for (int i = 0; i < nums.size(); ++i) count[nums[i]]++;
for (int i = 1; i <= nums.size(); ++i) {
if(count[i] == 2) ans.push_back(i);
}
return ans;
}
};
class Solution {
public:
vector<int> findDuplicates(vector<int>& nums) {
int n = nums.size();
for (auto& num: nums) {
int x = (num - 1) % n;
nums[x] += n;
}
vector<int> ret;
for (int i = 0; i < n; ++i) {
if (nums[i] > 2*n) ret.push_back(i + 1);
}
return ret;
}
};
仿41原地hash
class Solution {
public:
vector<int> findDuplicates(vector<int>& nums) {
int n=nums.size();
for(int i=0;i<n;i++) {
while(nums[i]!=nums[nums[i]-1]) swap(nums[i],nums[nums[i]-1]);
}
vector<int> res;
for(int i=0;i<n;i++) {
if(nums[i]!=i+1) res.push_back(nums[i]);
}
return res;
}
};
274 H 指数
H 指数
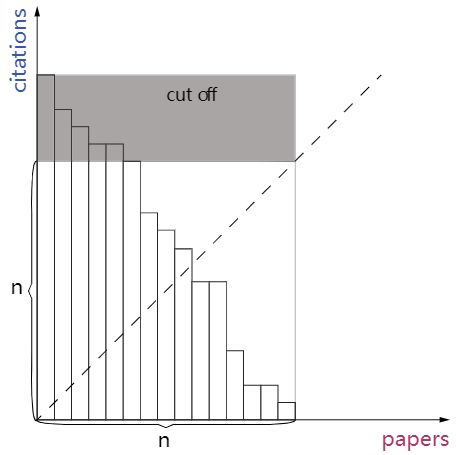
给定一位研究者论文被引用次数的数组(被引用次数是非负整数)。编写一个方法,计算出研究者的 h 指数。
h 指数的定义:h 代表“高引用次数”(high citations),一名科研人员的 h 指数是指他(她)的 (N 篇论文中)总共有 h 篇论文分别被引用了至少 h 次。且其余的 N - h 篇论文每篇被引用次数 不超过 h 次。
例如:某人的 h 指数是 20,这表示他已发表的论文中,每篇被引用了至少 20 次的论文总共有 20 篇。
示例:
输入:citations = [3,0,6,1,5]
输出:3
解释:给定数组表示研究者总共有 5 篇论文,每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
由于研究者有 3 篇论文每篇 至少 被引用了 3 次,其余两篇论文每篇被引用 不多于 3 次,所以她的 h 指数是 3。
提示:如果 h 有多种可能的值,h 指数是其中最大的那个
这里的提示起到一个迷惑的作用。
- 排序+线性扫描

首先将引用次数降序排序,在排完序的数组 citations 中,如果 citations[i]>i,那么说明第 0 到 i 篇论文都有至少 i+1 次引用。因此我们只要找到最大的 i 满足 citations[i]>i,那么 h 指数即为 i+1。
找到最大的 i 的方法有很多,可以对数组进行线性扫描,也可以使用二分查找。由于排序的时间复杂度已经为 O(nlogn),因此无论是线性扫描 O(n) 还是二分查找 O(logn),都不会改变算法的总复杂度。
class Solution {
public:
int hIndex(vector<int>& citations) {
sort(citations.begin(), citations.end());
int i = 0;
while(i < citations.size() && i < citations[citations.size() - 1 - i]) i++;
return i;
}
};
- 时间复杂度:O(nlogn),即为排序的时间复杂度。
- 空间复杂度:O(1)。大部分语言的内置 sort 函数使用堆排序,它只需要 O(1) 的额外空间。
- 计数
如果一篇文章的引用次数超过论文的总数 n,那么将它的引用次数降低为 n 也不会改变 h 指数的值。
class Solution {
public:
int hIndex(vector<int>& citations) {
int n = citations.size();
vector<int> papers(n + 1, 0);
for (auto c: citations) papers[min(n, c)]++;
int k = n;
for(int s = papers[n]; s < k; s += papers[k]) k--;
return k;
}
};
- 时间复杂度:O(n)。在计数时,我们仅需要遍历 citations 数组一次,因此时间复杂度为 O(n)。在找出最大的 k 时,我们最多需要遍历计数的数组一次,而计数的数组的长度为 O(n),因此这一步的时间复杂度为 O(n),即总的时间复杂度为 O(n)。
- 空间复杂度:O(n)。我们需要使用 O(n) 的空间来存放计数的结果。
- 排序+顺序遍历
如果引用次数大于等于后面剩余的文章数,h最大为剩余文章数目。返回就行了。例如[3,0,6,1,5],排序后是[0,1,3,5,6];
在遍历到3时,从此处到后面文章数目为3,则h为3.
class Solution {
public:
int hIndex(vector<int>& citations) {
sort(citations.begin(),citations.end());
for(int i=0;i<citations.size();++i){
if(citations[i]>=citations.size()-i) return citations.size()-i;
}
return 0;
}
};