学习笔记:《Short Randomizable Signatures》中的安全性证明
《Short Randomizable Signatures》中的安全性证明
- Assumptions
-
- EUF-CMA
- LRSW
- Assumption 1
- Assumption 2
- 证明假设成立
- 方案的安全性
-
- Single-Message Signature
- Multi-Message Signature
- Sequential Aggregate Signature
原方案https://blog.csdn.net/jiongxv/article/details/125261870
注意区分随机预言机模型与标准预言机模型:https://blog.csdn.net/weixin_43137080/article/details/109595044
这篇文章中涉及的安全性证明是without random oracles but in the generic group model
Assumptions
EUF-CMA
签名方案的标准安全概念是在选择消息攻击(EUF-CMA) [GMR88]下的存在不可伪造性,这意味着即使获得了对签名oracle的访问权,也很难为从未向签名oracle请求的消息m输出有效的签名对 ( m , σ ) (m,\sigma) (m,σ)。它被定义为挑战者 C \mathcal{C} C和敌手 A \mathcal{A} A之间的博弈:

如果没有概率多项式时间对手 A \mathcal{A} A能以不可忽略的概率获胜,则签名方案是EUF-CMA安全的.
LRSW
到目前为止,一个经典的假设是所谓的LRSW [LRSW00],它承认两个协议:
- issuing protocol:允许用户在消息 x x x上获得签名 σ \sigma σ,只需向签名者发送 x x x的承诺即可
- proving protocol:允许用户以零知识的方式证明他对 x x x承诺上的签名的知识。它们导致高效的匿名凭证
(LRSW Assumption) 设 G \mathbb{G} G是素数阶p的循环群,有一个生成元g。对于 X = g x X = g^x X=gx和 Y = g y Y = g^y Y=gy,其中 x x x和 y y y是 Z p \mathbb{Z}_p Zp中的随机标量。我们在输入 m ∈ Z p m\in \mathbb{Z}_p m∈Zp上定义oracle O ( m ) \mathcal{O}(m) O(m),它选择一个随机 h ∈ G h\in \mathbb G h∈G,输出三元组 T = ( h , h y , h x + m x y ) T = (h, h^y, h^{x+mxy}) T=(h,hy,hx+mxy)。给定 ( X , Y ) (X, Y) (X,Y)和对这个oracle的无限访问,没有敌手可以有效地为一个新标量 m ∗ m^* m∗生成这样的三元组,而不要求 O \mathcal{O} O。
Assumption 1
(Assumption 1).设 ( p , G 1 , G 2 , G T , e ) (p, \mathbb{G}_1, \mathbb{G}_2, \mathbb{G}_T, e) (p,G1,G2,GT,e)为Type-3(非对称, G 1 ≠ G 2 \mathbb{G}_1\neq\mathbb{G}_2 G1=G2)的双线性组设置, g g g (或 g ~ \widetilde g g ) 是 G 1 \mathbb{G}_1 G1 (或 G 2 \mathbb{G}_2 G2)的生成元。对于 ( X = g x , Y = g y ) (X = g^x,Y = g^y) (X=gx,Y=gy)和 ( X ~ = g ~ x , Y ~ = g ~ y ) , x , y ∈ Z p ( \widetilde X = \widetilde g^x, \widetilde Y = \widetilde g^y),x,y\in\mathbb Z_p (X =g x,Y =g y),x,y∈Zp, 在输入 m ∈ Z p m\in \mathbb{Z}_p m∈Zp上定义oracle O ( m ) \mathcal{O}(m) O(m),它选择一个随机 h ∈ G 1 h\in \mathbb G_1 h∈G1,输出元组 P = ( h , h x + m y ) P=(h,h^{x+my}) P=(h,hx+my)。给定 ( g , Y , g ~ , X ~ , Y ~ ) (g,Y,\widetilde g,\widetilde X, \widetilde Y) (g,Y,g ,X ,Y )和对这个oracle的无限访问,没有敌手可以有效地为一个新标量 m ∗ m^* m∗生成这样的元组,with h ≠ 1 G 1 h \neq 1_{\mathbb G_1} h=1G1,而不要求 O \mathcal{O} O。
可以注意到,使用pairing,可以检查敌手的输出,因为对 P = ( P 1 , P 2 ) P = (P_1, P_2) P=(P1,P2)应该满足 e ( P 1 , X ~ ⋅ Y ~ m ) = e ( P 2 , g ~ ) e(P_1,\widetilde X\cdot \widetilde Y^m)=e(P_2,\widetilde g) e(P1,X ⋅Y m)=e(P2,g ).
此外, ( X , Y ) (X, Y) (X,Y)足以回答oracle查询:在标量 m ∈ Z p m\in \mathbb{Z}_p m∈Zp上,计算 ( g r , ( X ⋅ Y m ) r ) (g^r,(X·Y^m)^r) (gr,(X⋅Ym)r)。这需要每个查询进行3次幂运算,而知道 ( x , y ) (x, y) (x,y)只需要在 G 1 \mathbb{G}_1 G1中进行随机抽样和一次幂运算。
在某些情况下,一个较弱的假设就足够了,即不给敌手 Y Y Y:
Assumption 2
(Assumption 2).设 ( p , G 1 , G 2 , G T , e ) (p, \mathbb{G}_1, \mathbb{G}_2, \mathbb{G}_T, e) (p,G1,G2,GT,e)为Type-3(非对称, G 1 ≠ G 2 \mathbb{G}_1\neq\mathbb{G}_2 G1=G2)的双线性组设置, g g g (或 g ~ \widetilde g g ) 是 G 1 \mathbb{G}_1 G1 (或 G 2 \mathbb{G}_2 G2)的生成元。对于 ( X = g ~ x , Y = g ~ y ) , x , y ∈ Z p (X = \widetilde g^x,Y = \widetilde g^y),x,y\in\mathbb Z_p (X=g x,Y=g y),x,y∈Zp, 在输入 m ∈ Z p m\in \mathbb{Z}_p m∈Zp上定义oracle O ( m ) \mathcal{O}(m) O(m),它选择一个随机 h ∈ G 1 h\in \mathbb G_1 h∈G1,输出元组 P = ( h , h x + m y ) P=(h,h^{x+my}) P=(h,hx+my)。给定 ( g ~ , X ~ , Y ~ ) (\widetilde g,\widetilde X, \widetilde Y) (g ,X ,Y )和对这个oracle的无限访问,没有敌手可以有效地为一个新标量 m ∗ m^* m∗生成这样的元组, with h ≠ 1 G 1 h \neq 1_{\mathbb G_1} h=1G1,而不要求 O \mathcal{O} O。
证明假设成立
Theorem 4.在一般双线性群模型中,上述假设1(因此假设2)成立:在 q q q 次oracle查询和 q G q_G qG 次group-oracle查询之后,没有敌手能够为一个新的标量以好于 6 ( q + q G ) 2 / p 6(q + q_G) ^2/p 6(q+qG)2/p的概率生成一个有效对.
Proof.
假设 r i ∈ Z p ∗ r_i \in \mathbb{Z}^∗_p ri∈Zp∗,第i次对 m i m_i mi的查询返回 ( h i , t i = h i ( x + y ⋅ m i ) ) , h i = g r i (h_i,t_i=h_i^{(x+y\cdot m_i)}),h_i=g^{r_i} (hi,ti=hi(x+y⋅mi)),hi=gri
我们必须首先证明敌手 A \mathcal A A不能符号化地产生一个新的有效元组,然后证明偶然有效性是非常不可能的。
对于标量 m ∗ m^* m∗上的输出元组 ( h ∗ , t ∗ ) (h ^*,t ^*) (h∗,t∗),由于 h ∗ , t ∗ ∈ G 1 h^*,t^*\in \mathbb G_1 h∗,t∗∈G1,所以它们只能是之前的元组 ( h i , t i ) , g , Y (h_i,t_i), g,Y (hi,ti),g,Y的组合(没有任何 G 2 \mathbb G_2 G2中的元素的帮助):它们是在 G 1 \mathbb G_1 G1中通过对内部规则的oracle的查询构建的,所以我们知道 ( ( u i , 1 , v i , 1 , u i , 2 , v i , 2 ) i , ( w 1 , w 2 ) , ( w 1 ′ , w 2 ′ ) ) ∈ Z p 4 q + 4 ((u_{i,1},v_{i,1},u_{i,2},v_{i,2})_i,(w_1,w_2),(w_1',w_2'))\in \mathbb Z_p^{4q+4} ((ui,1,vi,1,ui,2,vi,2)i,(w1,w2),(w1′,w2′))∈Zp4q+4满足:

因此,有新元组
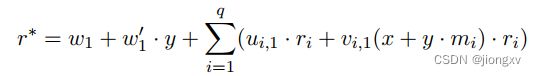
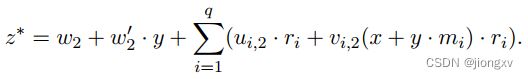
新元组的有效性意味着 z ∗ = r ∗ ( x + y ⋅ m ∗ ) z^*=r^*(x+y\cdot m^*) z∗=r∗(x+y⋅m∗),这导致:

为了使两个多变量多项式相等,两边应该出现相同的单项:
- 左边没有3次的单项式,所以对所有i, v i , 1 = 0 v_{i,1}=0 vi,1=0
- 右边没有 r i r_i ri的项,所以对所有i, u i , 2 = 0 u_{i,2}=0 ui,2=0
- 右边没有常数项,所以 w 2 = 0 w_2=0 w2=0
- 左边没有 x x x和 x y xy xy的项,所以 w 1 = 0 , w 1 ′ = 0 w_1=0,w_1'=0 w1=0,w1′=0:

- 右边没有 y y y的项了,所以 w 2 ′ = 0 w_2'=0 w2′=0:

- 对于所有的i, x r i xr_i xri的系数相等: v i , 2 = u i , 1 v_{i,2}=u_{i,1} vi,2=ui,1, y r i yr_i yri的系数: v i , 2 ⋅ m i = u i , 1 ⋅ m ∗ v_{i,2}\cdot m_i=u_{i,1}\cdot m^* vi,2⋅mi=ui,1⋅m∗
因为 r ∗ ≠ 0 r^*\neq 0 r∗=0(否则 h ∗ = 1 G 1 h^*=1_{\mathbb G_1} h∗=1G1),所以右边不等于0, v i , 2 = u i , 1 ≠ 0 v_{i,2}=u_{i,1}\neq0 vi,2=ui,1=0, m i = m ∗ m_i=m^* mi=m∗,这不是新的标量。
所以,敌手无法以符号化的方式为新标量生成有效的元组。
还需要评估偶然有效的概率:当两个不同的多项式涉及到对Oracle的回答时,得到相同的值。
- 由于oracle提供的元素与最多2阶多项式相关联(指被查询过的结果 ( h i , t i ) (h_i,t_i) (hi,ti)的系数 u i 1 , v i , 1 , u i , w , v i , 2 u_{i_1},v_{i,1},u_{i,w},v_{i,2} ui1,vi,1,ui,w,vi,2多项式),
- 由于公共元素与最多1阶多项式相关联(指公共元素 Y , g Y,g Y,g的系数 w 1 , w 2 , w 1 ′ , w 2 ′ w_1,w_2,w_1',w_2' w1,w2,w1′,w2′多项式),
- 从对不同组oracle的查询中得到的多项式最多3阶(因为配对查询)
(解释:公共元素就是group oracle,一阶表示只有一个变量,对应 q G q_G qG个结果;同理,由oracle提供的元素2阶表示两个结果,对应 2 q 2q 2q;而前文所述pairing中 g ~ \widetilde g g 等其他组oracle查询的多项式是3阶)
设 q G q_G qG为group-oracle查询的最大值,因此最多有 3 + 2 q + q G 3+2q +q_G 3+2q+qG多项式,所以最多 ( 3 + 2 q + q G ) 2 / 2 (3+2q +q_G)^2/2 (3+2q+qG)2/2对不同的多项式能求出相同的值.
根据Schwartz-Zippel引理, ( 3 + 2 q + q G ) 2 / 2 (3 + 2q + q_G)^2/2 (3+2q+qG)2/2个多项式的总概率上界为 3 / p × ( 3 + 2 q + q G ) 2 / 2 p 3/p\times(3 + 2q + q_G)^2/2p 3/p×(3+2q+qG)2/2p
3 ( 3 + 2 q + q G ) 2 / 2 p ≤ 6 ( q + q G ) 2 / p 3(3 + 2q + q_G)^2/2p \leq 6(q + q_G)^2/p 3(3+2q+qG)2/2p≤6(q+qG)2/p(放缩法),可以忽略不计。
(Schwartz-Zippel引理)

方案的安全性
Single-Message Signature
- 已经证明了Assumption 2是成立的,即如果有方案满足assumption2,则没有敌手能够成功伪造;single message是完全符合Assumption 2的
- 对于single message方案的EUF-CMA,query部分返回对Sign的oracle查询结果;等同于assumption 2。
- 所以,single message方案是满足EUF-CMA的
Multi-Message Signature
把这个多消息签名方案的安全性依赖于单消息签名方案的安全性,依此类推,假设2。
Theorem 6
在上述假设2下,多消息签名方案满足EUF-CMA安全级别。
更准确地说,如果攻击者能够以 ϵ \epsilon ϵ的概率攻破多消息签名方案的EUF-CMA安全性,则在相同的运行时间和相同的签名查询次数内,存在攻击者攻破单消息签名方案的EUF-CMA安全性,且成功的概率大于 ϵ − q / p \epsilon-q/p ϵ−q/p
Proof.
假设 A \mathcal A A是多消息签名方案的EUF-CMA安全性的敌手。针对单消息签名方案的EUF-CMA安全性,使用 A \mathcal A A构造一个归约 R \mathcal R R。后一场game的挑战者将用 C \mathcal C C表示.
- Setup. R \mathcal R R从 C \mathcal C C接收到一个公钥 p k ∗ {\rm pk^*} pk∗,其中包含签名方案的公共参数 p p pp pp和 ( g ~ , X ~ , Y ~ ) (\widetilde g,\widetilde X, \widetilde Y) (g ,X ,Y )。它选择 α j , β j ← Z p , j = 1 , . . . , r \alpha_j,\beta_j\leftarrow \mathbb Z_p,j=1,...,r αj,βj←Zp,j=1,...,r,令 Y ~ j ← Y ~ α j g ~ β j \widetilde Y_j\leftarrow \widetilde Y^{\alpha_j}\widetilde g^{\beta_j} Y j←Y αjg βj。输出公钥 p k ← ( g ~ , X ~ , Y ~ 1 , . . . , Y ~ r ) pk\leftarrow(\widetilde g,\widetilde X,\widetilde Y_1,...,\widetilde Y_r) pk←(g ,X ,Y 1,...,Y r)
- Queries. 当 A \mathcal A A查询一个向量 M i = ( m i , 1 , . . . , m i , r ) M_i=(m_{i,1},...,m_{i,r}) Mi=(mi,1,...,mi,r)上的签名时, R \mathcal R R首先向 C \mathcal C C请求一个 m i = ∑ α j m i , j m_i=\sum\alpha_jm_{i,j} mi=∑αjmi,j上的签名 σ = ( σ 1 , σ 2 ) \sigma=(\sigma_1,\sigma_2) σ=(σ1,σ2) ,从而 e ( σ 1 , X ~ ⋅ Y ~ ∑ α j m i , j ) = e ( σ 2 , g ~ ) e(\sigma_1,\widetilde X\cdot\widetilde Y^{\sum\alpha_jm_{i,j}})=e(\sigma_2,\widetilde g) e(σ1,X ⋅Y ∑αjmi,j)=e(σ2,g ).接着,计算 σ 2 ′ ← σ 2 ⋅ σ 1 ∑ β j ⋅ m i , j \sigma_2'\leftarrow\sigma_2\cdot\sigma_1^{\sum \beta_j\cdot m_{i,j}} σ2′←σ2⋅σ1∑βj⋅mi,j并返回有效签名 ( σ 1 , σ 2 ′ ) (\sigma_1,\sigma_2') (σ1,σ2′)给 A \mathcal A A:

- Output. 最终, A \mathcal A A在向量 M ∗ = ( m 1 ∗ , . . . , m r ∗ ) M ^*=(m_1^*,...,m_r^*) M∗=(m1∗,...,mr∗)上输出签名 σ = ( σ 1 , σ 2 ) \sigma=(\sigma_1,\sigma_2) σ=(σ1,σ2)。签名 σ \sigma σ是一个有效的伪造,如果:

如果对于某些 i = { 1 , . . . , q } i=\{1,...,q\} i={1,...,q}, ∑ α j m j ∗ = ∑ α j m i , j , R \sum \alpha_jm_j^*=\sum\alpha_jm_{i,j},\mathcal R ∑αjmj∗=∑αjmi,j,R中止。
否则,输出 σ ∗ = ( σ 1 ∗ , σ 2 ∗ ) : σ 1 ∗ ← σ 1 , σ 2 ∗ ← σ 2 ⋅ σ 1 − ∑ β j ⋅ m j ∗ , m ∗ ← ∑ α j m j ∗ \sigma^*=(\sigma_1^*,\sigma_2^*):\sigma_1^*\leftarrow \sigma_1,\sigma_2^*\leftarrow\sigma_2\cdot\sigma_1^{-\sum\beta_j\cdot m_j^*},m^*\leftarrow\sum\alpha_jm_j^* σ∗=(σ1∗,σ2∗):σ1∗←σ1,σ2∗←σ2⋅σ1−∑βj⋅mj∗,m∗←∑αjmj∗:

因为消息 m ∗ m^* m∗从未查询过,所以这是一个有效的伪造签名。
分析: - query阶段,敌手 A \mathcal A A经过q次查询,获得对于消息 M i = ( m i , 1 , . . . , m i , r ) M_i=(m_{i,1},...,m_{i,r}) Mi=(mi,1,...,mi,r)的合法multi message签名;
- output阶段,先假设敌手 A \mathcal A A能输出对于新消息 M ∗ = ( m 1 ∗ , . . . , m r ∗ ) M ^*=(m_1^*,...,m_r^*) M∗=(m1∗,...,mr∗)合法的multi message签名,再证明可以利用这组签名伪造single messge签名
- 命题:多消息伪造 → \rightarrow →单消息伪造;逆否命题:单消息不可伪造 → \rightarrow →多消息不可伪造
- 注意:如果出现 ∑ α j m j ∗ = ∑ α j m i , j \sum \alpha_jm_j^*=\sum\alpha_jm_{i,j} ∑αjmj∗=∑αjmi,j,表示用multi message组合而成的single message已经查询过了,不符合EUF-CMA的要求,所以中止这种巧合。
证明这种线性关系几乎不可能出现:
(要区分 R \mathcal R R和 A \mathcal A A的视角, α j \alpha_j αj是由 R \mathcal R R选择的, A \mathcal A A得到的公钥中包含 α j \alpha_j αj,分析这种“包含”是否导致公钥和 α j \alpha_j αj之间存在某种联系,即 A \mathcal A A是否能从中获得某些知识)
设标量 y , Y ~ = g ~ y y,\widetilde Y=\widetilde g^y y,Y =g y,随机选择 γ j ← Z p , j = 1 , . . . , r \gamma_j\leftarrow\mathbb Z_p,j=1,...,r γj←Zp,j=1,...,r,设 α j ′ ← α j − γ j , β j ′ ← β j + y γ j , j = 1 , . . . , r \alpha_j'\leftarrow\alpha_j-\gamma_j,\beta_j'\leftarrow\beta_j+y\gamma_j,j=1,...,r αj′←αj−γj,βj′←βj+yγj,j=1,...,r,可以注意到:
![]()
因此,公钥是独立于实际的 γ j \gamma_j γj的,因此没有揭示 α j \alpha_j αj的信息,这与仅依赖于oracle和公钥选择的 σ 1 \sigma_1 σ1的签名是一样的。
因此,敌手的完整视图完全独立于 α j \alpha_j αj的视图。因此, R \mathcal R R中止的概率的上限(多项式Schwartz-Zippel引理)是 q × 1 / p = q / p q\times 1/p=q/p q×1/p=q/p。
结论 R \mathcal R R成功将攻破multi message签名规约到攻破single message签名的概率大于 ϵ − q / p \epsilon-q/p ϵ−q/p.证毕。
Sequential Aggregate Signature
在认证公钥设置中,我们将这个聚合签名方案的安全性依赖于单消息签名方案的安全性,依此类推假设2:
Theorem 7. 在上述假设2下,在认证公钥设置下,聚合签名方案达到EUF-CMA安全级别。更准确地说,如果攻击者能够破坏聚合签名方案的EUF-CMA安全性,则存在攻击单消息签名方案的EUF-CMA安全性的攻击者,在相同的运行时间和相同的签名查询次数内,以相同的概率成功。
Proof.
在认证公钥设置中,假设 A \mathcal A A是聚合签名方案的EUF-CMA安全性的敌手。针对单消息签名方案的EUF-CMA安全性,使用 A \mathcal A A构造一个归约 R \mathcal R R。后一场game的挑战者将用 C \mathcal C C表示.
- Setup. R \mathcal R R首先将密钥列表KeyList初始化为空。然后,从 C \mathcal C C中获取一个公钥 p k {\rm pk} pk,其中包含签名方案的公共参数 p p pp pp和 ( g ~ , X ~ , Y ~ ) (\widetilde g,\widetilde X, \widetilde Y) (g ,X ,Y )
- 请求 C \mathcal C C在0上签名,返回 τ = ( τ 1 , τ 2 ) \tau=(\tau_1,\tau_2) τ=(τ1,τ2)使 e ( τ 1 , X ~ ) = e ( τ 2 , g ~ ) e(\tau_1,\widetilde X)=e(\tau_2,\widetilde g) e(τ1,X )=e(τ2,g ) ,可以设置 g ← τ 1 g\leftarrow \tau_1 g←τ1和 X ← τ 2 X\leftarrow \tau_2 X←τ2
- 将聚合签名方案的公共参数设为 ( p p , g , X , g ~ , X ~ ) (pp,g,X,\widetilde g,\widetilde X) (pp,g,X,g ,X ),并将 p k ∗ ← Y ~ {\rm pk} ^*\leftarrow\widetilde Y pk∗←Y 发送给 A \mathcal A A。在下面, x ∗ x^ * x∗和 y ∗ y ^* y∗将表示(未知)标量,使 X ~ = g ~ x ∗ \widetilde X=\widetilde g^{x^*} X =g x∗(及 X = g x ∗ X=g^{x^*} X=gx∗), Y ~ = g ~ y ∗ \widetilde Y=\widetilde g^{y^*} Y =g y∗.因此,标量 y ∗ y^* y∗是与 p k ∗ pk^* pk∗相关联的未知密钥 s k ∗ sk^* sk∗(注意 R \mathcal R R可以请求 C \mathcal C C的查询和公共信息,但并不知道single message的私钥等)。
- Join Query.
当 A \mathcal A A要求添加一个公钥 p k i pk_i pki时,认证过程包括对相关密钥 s k i sk_i ski的知识证明,允许 R \mathcal R R提取它:它将 p k i pk_i pki存储在KeyList中,并将 ( s k i , p k i ) (sk_i,pk_i) (ski,pki)存储在其自己的签名/验证密钥列表中,以供将来的模拟使用 - Signature Query.
- 当 A \mathcal A A请求将消息 m i m_i mi聚合到公共密钥 ( p k i , 1 , . . . , p k i , r i ) (pk_{i,1},...,pk_{i,r_i}) (pki,1,...,pki,ri)下消息 ( m i , 1 , . . . , m i , r i ) (m_{i,1},...,m_{i,r_i}) (mi,1,...,mi,ri)上的聚合签名 σ i \sigma_i σi上时,如果 r i > 0 r_i>0 ri>0, R \mathcal R R首先检查 σ i \sigma_i σi的有效性,并在否定的情况下中止。
- 请求 C \mathcal C C在 m i m_i mi上签名,返回 σ = ( σ 1 , σ 2 ) \sigma = (\sigma_1,\sigma_2) σ=(σ1,σ2)
- 聚合签名中涉及的所有公钥必须事先经过认证,然后 R \mathcal R R知道相关的密钥 ( s k i , 1 , . . . , s k i , r i ) = ( y i , 1 , . . . , y i , r i ) (sk_{i,1},...,sk_{i,r_i}) = (y_{i,1},...,y_{i,r_i}) (ski,1,...,ski,ri)=(yi,1,...,yi,ri):它随机选择一个 t ← Z p t\leftarrow\mathbb Z_p t←Zp并返回 σ ′ ← ( σ 1 t , ( σ 2 ⋅ σ 1 ∑ j = 1 r i y i , j ⋅ m i , j ) t ) \sigma'\leftarrow(\sigma_1^t,(\sigma_2\cdot \sigma_1^{\sum_{j=1}^{r_i}y_{i,j}\cdot m_{i,j}})^t) σ′←(σ1t,(σ2⋅σ1∑j=1riyi,j⋅mi,j)t)。这个签名满足:

它是在公钥 ( ( p k i , j ) i , p k i ∗ ) ((pk_{i,j})_i,pk_i^*) ((pki,j)i,pki∗)下,对向量 ( ( m i , j ) i , m i ) ((m_{i,j})_i,m_i) ((mi,j)i,mi)的有效签名.
分析:(这是不是查询并生成合法聚合签名的过程?)
已知一个对单消息 m i m_i mi的签名, ( σ 1 , σ 2 = σ 1 x + y i ) (\sigma_1,\sigma_2=\sigma_1^{x+y_i}) (σ1,σ2=σ1x+yi)
根据聚合签名的原始定义,首先要构造一个将消息 m i m_i mi聚合到公共密钥 ( p k i , 1 , . . . , p k i , r i ) (pk_{i,1},...,pk_{i,r_i}) (pki,1,...,pki,ri)下消息 ( m i , 1 , . . . , m i , r i ) (m_{i,1},...,m_{i,r_i}) (mi,1,...,mi,ri)上的聚合签名 σ i \sigma_i σi:
- j = 0 , σ i , 0 = ( g , X ) j=0,\sigma_{i,0}=(g,X) j=0,σi,0=(g,X)
- j = 1 , σ i , 1 = ( g t i , 1 , ( X ⋅ g y i , 1 m i , 1 ) t i , 1 ) j=1,\sigma_{i,1}=(g^{t_{i,1}},(X\cdot g^{y_{i,1}m_{i,1}})^{t_{i,1}}) j=1,σi,1=(gti,1,(X⋅gyi,1mi,1)ti,1)
- j = 2 , σ i , 2 = ( g t i , 1 t i , 2 , ( X ⋅ g y i , 1 m i , 1 + y i , 2 m i , 2 ) t i , 1 t i , 2 ) j=2,\sigma_{i,2}=(g^{t_{i,1}t_{i,2}},(X\cdot g^{y_{i,1}m_{i,1}+y_{i,2}m_{i,2}})^{t_{i,1}t_{i,2}}) j=2,σi,2=(gti,1ti,2,(X⋅gyi,1mi,1+yi,2mi,2)ti,1ti,2)
- …
- j = r i , σ i = ( g ∏ j t i , j , ( X ⋅ g ∑ j y i , j m i , j ) ∏ j t i , j ) = j=r_i,\sigma_i=(g^{\prod_j t_{i,j}},(X\cdot g^{\sum_j y_{i,j}m_{i,j}})^{\prod_j t_{i,j}})= j=ri,σi=(g∏jti,j,(X⋅g∑jyi,jmi,j)∏jti,j)= ( σ 1 , σ 1 x + ∑ j y i , j m i , j ) (\sigma_1,\sigma_1^{x+\sum_j y_{i,j}m_{i,j}}) (σ1,σ1x+∑jyi,jmi,j)(用 σ 1 \sigma_1 σ1表示了 g ∏ j t i , j g^{\prod_j t_{i,j}} g∏jti,j)
- 那么后面也要变换: σ ′ = ( σ 1 t , σ 2 ′ ) \sigma'=(\sigma_1^t,\sigma_2') σ′=(σ1t,σ2′), σ 2 ′ = ( σ 2 ⋅ σ 1 y i m i ) t = ( σ 1 x + ∑ j y i , j m i , j ⋅ σ 1 y i m i ) t = ( σ 2 m i ⋅ σ 1 ∑ j y i , j m i , j ) t \sigma_2'=(\sigma_2\cdot\sigma_1^{y_im_i})^t=(\sigma_1^{x+\sum_j y_{i,j}m_{i,j}}\cdot\sigma_1^{y_im_i})^t=(\sigma_2^{m_i}\cdot\sigma_1^{\sum_j y_{i,j}m_{i,j}})^t σ2′=(σ2⋅σ1yimi)t=(σ1x+∑jyi,jmi,j⋅σ1yimi)t=(σ2mi⋅σ1∑jyi,jmi,j)t
- Output.
A \mathcal A A最终在公钥 ( p k 1 , . . . , p k r ) (pk_1,...,pk_r) (pk1,...,pkr)下的消息 ( m 1 ∗ , . . . , m r ∗ ) (m_1^*,...,m_r^*) (m1∗,...,mr∗)上输出一个聚合签名 σ = ( σ 1 , σ 2 ) \sigma=(\sigma_1,\sigma_2) σ=(σ1,σ2)。当满足以下条件时,聚合签名σ是一个有效的伪造:

1代表 e ( σ 1 , X ~ ⋅ ∏ p k j m j ∗ ) = e ( σ 2 , g ~ ) e(\sigma_1,\widetilde X\cdot\prod pk_j^{m_j^*})=e(\sigma_2,\widetilde g) e(σ1,X ⋅∏pkjmj∗)=e(σ2,g )
2代表 R \mathcal R R知道所有 y j y_j yj满足 p k j = g ~ y j , j = 1 , . . . , r pk_j=\widetilde g^{y_j},j=1,...,r pkj=g yj,j=1,...,r且 p k j ≠ p k ∗ pk_j\neq pk^* pkj=pk∗
3代表在 1 , . . . , r 1,...,r 1,...,r中有一个唯一的 j ∗ j^* j∗, p k j ∗ pk_{j^*} pkj∗,对应未查询过的 m j ∗ m_{j^*} mj∗
(下面构造single message的伪造)
R \mathcal R R可以计算 σ ∗ = ( σ 1 ∗ ← σ 1 , σ 2 ∗ ← σ 2 ⋅ ∏ j ≠ j ∗ σ 1 − y j ⋅ m j ∗ ) \sigma^*=(\sigma_1^*\leftarrow\sigma_1,\sigma_2^*\leftarrow\sigma_2\cdot\prod_{j\neq j^*}\sigma_1^{-y_j\cdot m_j^*}) σ∗=(σ1∗←σ1,σ2∗←σ2⋅∏j=j∗σ1−yj⋅mj∗)满足:

分析:(这是不是构造了一个有效的单消息签名伪造?)
σ ∗ = ( σ 1 ∗ ← σ 1 , σ 2 ∗ ← σ 2 ⋅ ∏ j ≠ j ∗ σ 1 − y j ⋅ m j ∗ ) = ( σ 1 , σ 1 x + ∑ j ≠ j ∗ p k j m j ∗ + p k j ∗ m j ∗ ∗ ⋅ σ 1 ∑ j ≠ j ∗ − y j ⋅ m j ∗ ) = ( σ 1 , σ 1 x + p k j ∗ m j ∗ ∗ ) \begin{aligned} \sigma^*&=(\sigma_1^*\leftarrow\sigma_1,\sigma_2^*\leftarrow\sigma_2\cdot\prod_{j\neq j^*}\sigma_1^{-y_j\cdot m_j^*})\\ &=(\sigma_1,\sigma_1^{x+\sum_{j\neq j^*}pk_jm_j^*+pk_{j^*}m_{j^*}^*}\cdot\sigma_1^{\sum_{j\neq j^*}-y_j\cdot m_j^*})\\ &=(\sigma_1,\sigma_1^{x+pk_{j^*}m_{j^*}^*}) \end{aligned} σ∗=(σ1∗←σ1,σ2∗←σ2⋅j=j∗∏σ1−yj⋅mj∗)=(σ1,σ1x+∑j=j∗pkjmj∗+pkj∗mj∗∗⋅σ1∑j=j∗−yj⋅mj∗)=(σ1,σ1x+pkj∗mj∗∗)
是构造了一个有效的未查询过的单消息签名。
但是必须另外证明签名查询是用 σ ′ ← ( σ 1 t , ( σ 2 ⋅ σ 1 ∑ j = 1 r i y i , j ⋅ m i , j ) t ) \sigma'\leftarrow(\sigma_1^t,(\sigma_2\cdot \sigma_1^{\sum_{j=1}^{r_i}y_{i,j}\cdot m_{i,j}})^t) σ′←(σ1t,(σ2⋅σ1∑j=1riyi,j⋅mi,j)t)正确模拟的, σ = ( σ 1 , σ 2 ) \sigma= (\sigma_1,\sigma_2) σ=(σ1,σ2)是在 p k ∗ pk^* pk∗下 m 1 m_1 m1的签名, t t t是一个随机标量,而真正的签名应该是 σ ′ ← ( σ i , 1 t , ( σ i , 2 ⋅ σ i , 1 y ⋅ m ) t ) \sigma'\leftarrow(\sigma_{i,1}^t,(\sigma_{i,2}\cdot \sigma_{i,1}^{y\cdot m})^t) σ′←(σi,1t,(σi,2⋅σi,1y⋅m)t),其中 σ i = ( σ i , 1 , σ i , 2 ) \sigma_i= (\sigma_{i,1},\sigma_{i,2}) σi=(σi,1,σi,2)是公钥 ( p k i , 1 , . . . , p k i , r i ) (pk_{i,1},...,pk_{i,r_i}) (pki,1,...,pki,ri)下消息 ( m i , 1 , . . . , m i , r i ) (m_{i,1},...,m_{i,r_i}) (mi,1,...,mi,ri)上的有效签名(或当 r = 0 r = 0 r=0时 σ i = ( g , X ) \sigma_i = (g,X) σi=(g,X)), t t t是一个随机标量。
但可以注意到,在这两种情况下, σ 1 ′ \sigma_1' σ1′是 G 1 ∗ \mathbb G _1^* G1∗中的一个随机元素,而 σ 2 ′ \sigma_2' σ2′是满足 e ( σ 2 ′ , g ~ ) = e ( σ 1 ′ , X ~ ⋅ ∏ j = 1 r i p k i , j m i , j ⋅ p k m i ) e(\sigma_2',\widetilde g) = e(\sigma_1', \widetilde X\cdot \prod_{j=1}^{r_i} pk_{i,j}^{m_{i,j}}\cdot pk^{m_i}) e(σ2′,g )=e(σ1′,X ⋅∏j=1ripki,jmi,j⋅pkmi)的唯一元素。因此,完美的模拟。
结论:多消息伪造 → \rightarrow →单消息伪造;逆否命题:单消息不可伪造 → \rightarrow →多消息不可伪造