计算机组成与设计:硬件/软件接口，第三章详细梳理，附思维导图

三、计算机的运算

章节导图

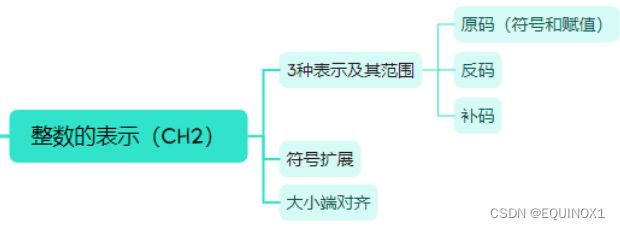
一、整数的表示

无符号整数 原码 反码

不同于MIPS的32位字，我们先讨论8位整数
将全部8位用来表示绝对值的二进制数叫做无符号整数
其表示范围为0~+255 (2^8-1)
00000000 00000001 0000001…1 11111 1 1

将最高位用来表示正负号(正数为0,负数为1)，其余7位表示绝对值的方法叫做原码也称为符号和幅值表示法，其表示范围为-127_-0+0~+127 (2^7-1)
00000000 00000001 000000…01111111 10000000 10000001 …1111111 1

*原码是带符号整数的表示方法

将最高位为0的原码按位取反来表示负数，叫做反码

其表示范围为 -127~ -0 ~ +0 ~+127

00000000 00000001 00000010 …… 01111111 11111111 11111110 …… 10000000

原码和反码在当今计算机中并没有广泛应用，因为其不能很好的表示二进制运算，反码更是还有+0和-0之分

补码符号扩展大小端编址

原码和反码不能直接用于二进制加减法，且正负两个0会给编程人员带来麻烦
因此，当今计算机都采用可以直接加减的补码来表示带符号整数
先用00000000_{01111111表示零和正整数0} +127
再用10000000~11111111表示负数-128 (-2^7) ~-1
数x和它的反码相加，必定是11111111 (-1)
即x + ~x = -1, ~x+1=x , 因此将一个补码整数化为它的相反数,方法就是按位取反再+1

addi指令中，第一个源操作数是32位补码寄存器， 第二个源操作数是16位补码立即数，我们为了将这个16位的立即数字段加到32位的寄存器上去，需要把这个16位的数转换为数值上相等的32位的数，方法就是将原有的16位数复制到32位新数的低16位，再将最高位即符号位，复制到高16位，即可完成符号扩展

这种方法之所以正确，是因为二进制补码表示的正数实际上在左侧有无限多个0，而负数在左侧有无限多个1。只是为了适应硬件的宽度，数的前导位被隐藏了，符号扩展只是简单地恢复了其中一部分。

补码的意义

我们都知道补码是由原码取反+1得来，但其意义是什么？为什么补码可以更好地表示二进制运算？这里简单说明一下。

对于我们日常生活中的钟表，当时针指向3时，我们想要时针指向12，一般情况下对于顺时针方向转动的时钟来讲，我们需要等待时针再走9个小时才能到达12，可如果忽略旋转规则，我们发现让时针逆时针走3个小时也能指向12，这说明在一圈为12小时的表盘上，减3和加9的结果是一样的，了解这个之后，我们再回到补码上

就像钟表顺时针加9和逆时针减3得到同样结果，假设我们有n位的二进制数字a和b，我们要完成a - b操作，我们是不是也可以仿照钟表，把a - b等效为 a + 2 ^ n - b呢，如果你想明白了这一点，我们前面不是说了x + ~x = -1(补码) 即 2 ^ n - 1吗，这就说明减去一个数字等效于加上它的补码，只不过我们注意控制下符号就好了

对于一个长于1字节的整数，如果高位放在低地址，就称为大端编址
如果高位放在高地址，就称为小端编址

比如：对于32位16进制 0x12345678 这是我们习惯的书写顺序，现在我们假设有一段连续内存，左侧为低地址，右侧为高地址

那么大端编址：0x12345678 小端编址：0x78563412

那么我们如何知道自己电脑是大端还是小端编址呢？

以C/C++为例，我们可以把上面的数字0x12345678的第一个字节取出来打印一下

C语言则可以使用printf格式化输出

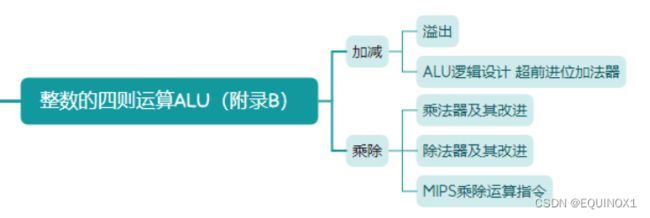
二、整数的四则运算 ALU

补码加减法 溢出

列二进制竖式计算 :
12+3=15 (00001100+00000011)
120+15=135 (01111000+00001111 )
-100-50=-150 (10011100-00110010)

第二个式子(正+正) 超出了127的上限，对符号位产生进位,称为上溢
第三个式子(负-正) 超出了-128的下限，对符号位产生借位，称为下溢
还有哪种情况可能出现。上溢或下溢?

对于加法，符号相同会溢出 对于减法，符号相反会溢出

上溢和下溢统称为溢出，表现为对符号位进位或借位，符号错误

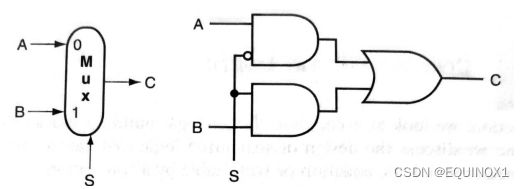
多路选择器

译码器(decoder) 有n个输入和2"个输出，根据输入的数字将-个输出信号置位1
多路选择器(multiplexer) 有n个输入数据和1个输出数据.
根据选择控制信号的数字，决定将哪一个输入作为输出

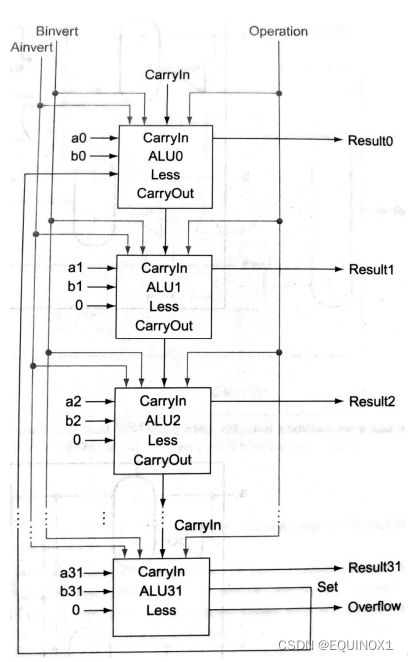
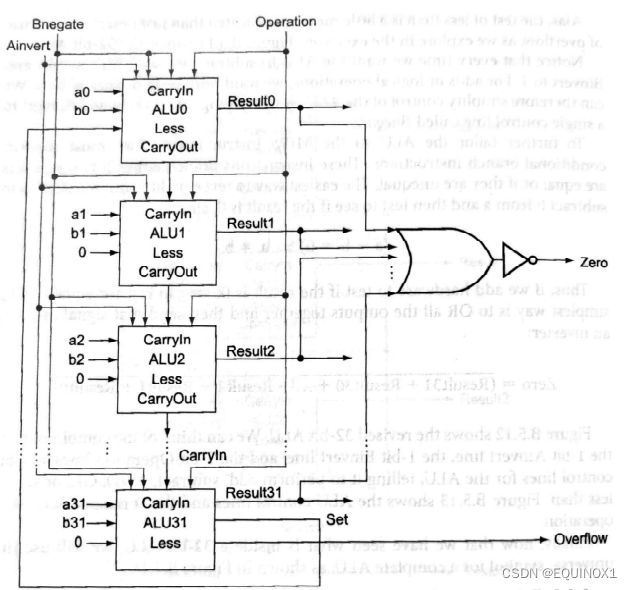
32位ALU:行波进位

将32个1位ALU拼接起来就形成了32位ALU，低位的进位输出指向高位的进位输入，低位的进位输入用于控制减法，为了支持sIt指令实现条件分支，若rs-rt的符号位为1,差为负数，小于关系成立，将这个置位标志1从最高位指向最低位的Less信号，反之，将置位标志0指向最低位Less信号，高31位Less信号恒定为0，为了实现溢出检测，最高位ALU添加了溢出检测逻辑，输出溢出信号

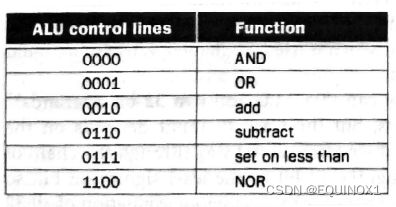
32位ALU:控制信号

为了支持条件分支beq、bne，需要判定两源操作数相减是否为0，对32位结果一并进行或非操作，当且仅当结果为32位0时，零标志为1

由于B取反和用于减法的最低为进位输入，在减法时同时为1，在其他时候互不干扰，可以合并为一根控制线Bnegate信号

ALU符号图加法器的改进:超前进位

进位速度制约了加法的速度，32位ALU的行波进位方式意味着每次进位都要通过与门、或门各一次，共产生64个门延迟，为了加快进位、进而加快加法运算，现在广泛采用超前进位加法器(carry-lookahead adder)，通过将进位分为4位一组， 抽象成每组的进位，实现加法器的并行执行

具体原理比较复杂，记住结论:要执行n位加法，求出n是4的几次方并向上取整,再乘2加1，就是超前进位的门延迟以16位、64位、32位加法为例分析， 并计算加速比

乘法

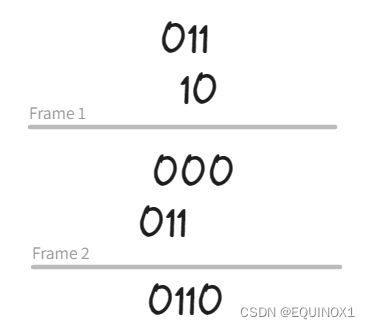
列四位二进制竖式计算2x3

教材将前一个乘数称为被乘数,后一个称为乘数
被乘数乘以乘数某位的结果称为中间积
二进制的中间积要么是被乘数及其左移后的结果，要么是0

乘法器

两32位数相乘，乘数用32位的乘数寄存器即可
被乘数从低32位逐次到高32位，需要64位被乘数寄存器
积最大位数 = 被乘数位数 + 乘数的位数，需要64位积寄存器

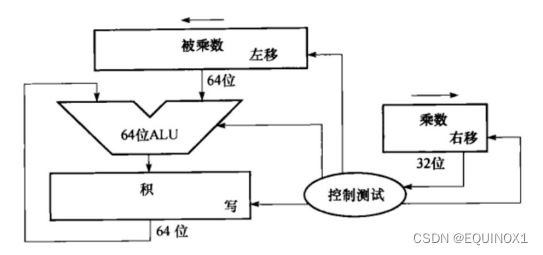
改进的乘法器

上述乘法器将三个步骤执行32轮，大约需要100个时钟周期，且寄存器空间浪费较大
注意到每进行一轮迭代，乘积位数从32增长到64,乘数位数从32减少到0
合起来总是64位，可以拼接成一个64位乘积/乘数寄存器
让积相对于被乘数右移(而不是被乘数相对于积左移)，ALU从64位缩减到32位
改进后硬件规模大大减小，每一步可以仅占一时钟周期

除法

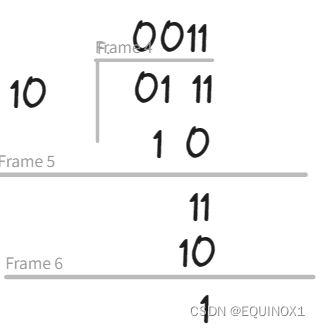
列竖式计算7/2

在任何情况下，整数除法都要满足被除数=除数x商+余数
计算-7/2时，可以商-3余-1,也可以商-4余1
为了避免这种差异，规定余数和被除数同号，即商-3余-1

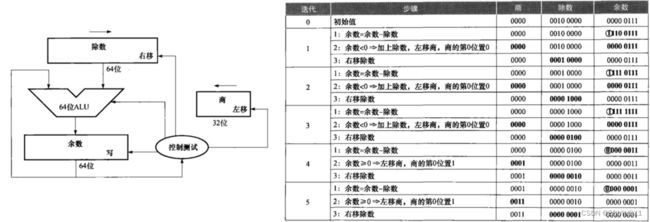
除法器

被除数一开始存在64位余数寄存器中， 除数从64位除数寄存器的高32位逐次右移到低32位
每次迭代，向32位商寄存器的最低位添加0或1

注意，改进前的除法器一 共进行33次(n+1次) 迭代

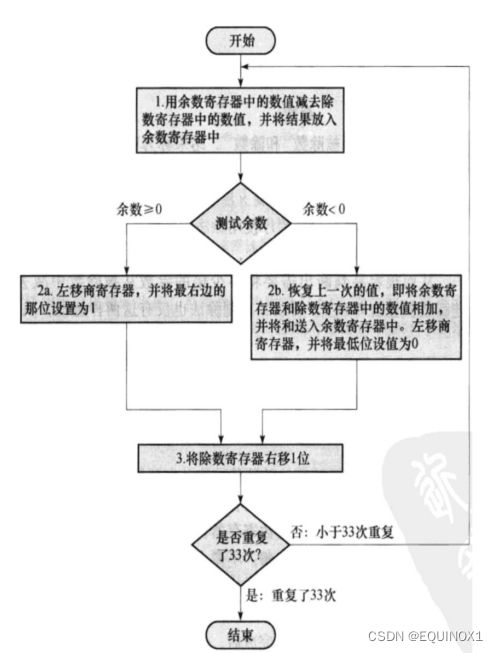
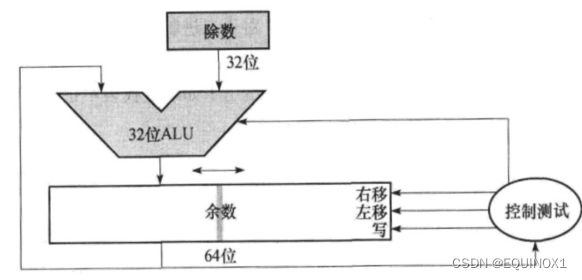
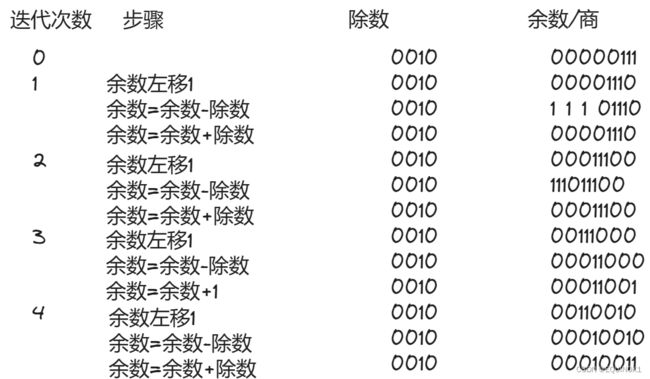
改进的除法器

同样，上述除法器效率低、寄存器空间浪费大
通过扩充控制逻辑，除法可以在改进的乘法器硬件中完成
注意到每轮迭代，余数(一开始是被除数)位数从64减少到32，商的位数从0增加到32
合起来总是64位，可以拼接成一个64位余数/商寄存器 ，最后的余数即为整个除法的余数
ALU只对高32位进行减法
*和改进前不同，只进行32次(n次)迭代

乘除法的进一.步改进MIPS乘除运算指令

乘法和除法都通过记忆符号、将操作数转化为自然数、再进行运算，最后对负数结果取反
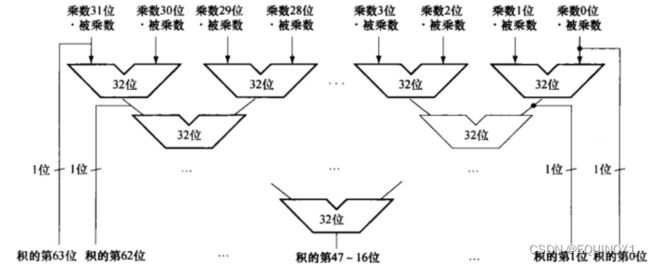
为了进一步加快乘法运算, 可以采用31个ALU拼接成并行树乘法器
SRT除法算法通过查表来预测每步有几个商位，每步生成多个商位
超前进位加法器、并行树、SRT, 都借助摩尔定律提供的丰富硬件资源加大电路规模来加速，属于用空间换时间的加速策略

MIPS提供mult multu div divu
四条乘除运算指令，均为双操作数R型指令
对乘法，Hi, Lo = reg1 x reg2
对除法，Hi = reg1 % reg2
Lo = reg1 / reg2
从Hi中获得mfhi、从Lo中获得mflo
均为单操作数R型指令

复习题

1、补码加减的溢出分为哪两种，分别对应哪四个情况?

上溢和下溢 上溢：正 + 正 正 - 负 下溢：负 - 正 负 + 负

2、为什么最低位ALU不接收进位,也要使用全加器?
3、为了支持and、or运算,采用哪种数字电路部件来选择信号? nor运算怎么实现?
4、32位ALU怎样支持sIt和条件分支指令?
5、三组(四位) ALU控制信号的作用分别是什么?
6、行波进位和超前进位加法器的门延迟分别怎么计算?

行波进位：位数 * 2(一个与门一个或门) 超前进位加法器：[log4 位数] * 2 + 1

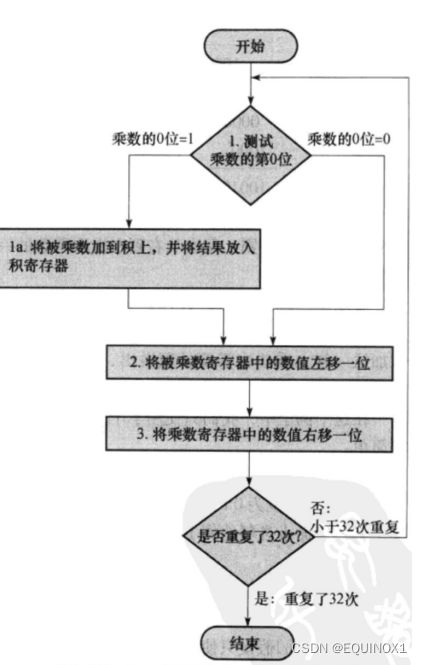
7、改进前的乘法器，控制逻辑实现哪些功能?

1、根据乘数最低位决定是否将被乘数加到积上

2、被乘数左移，乘数右移

3、计数

8、改进后的乘法器和除法器是否可以共用一套硬件? 64位寄存器怎么变化?

可以

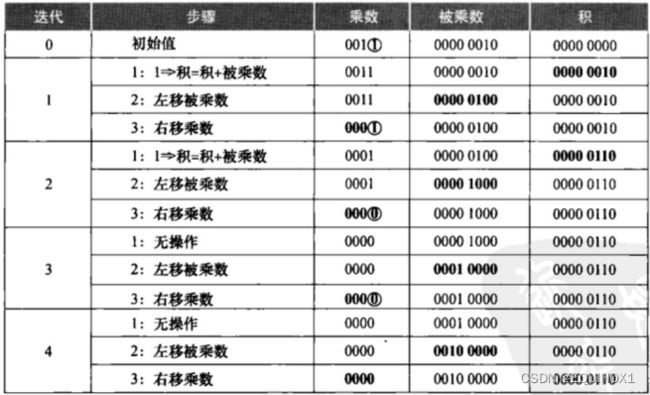
*9、熟练掌握分步列出改进后的乘除法器中寄存器的值
10、乘法、除法分别用什么策略实现进一 步改进?

并行树 SRT

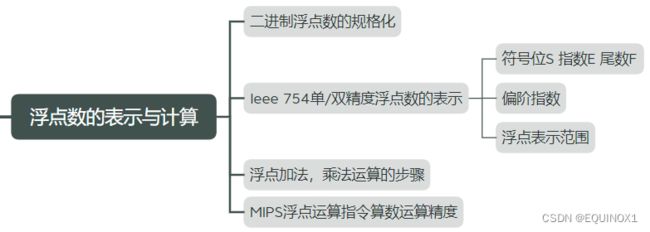
三、浮点数的表示与运算

浮点数规格化1EEE754单精度浮点数

为了表示非整数实数,现在的计算机广泛采用小数点浮动的浮点数(float point number)

以十进制小数-0.75为例
首先，转化为二进制实数(小数)
然后，将二进制实数表示为以2为基数的科学记数法，这个过程称为规格化
这时我们得到三个重要信息:①实数的正负②小数点右边的尾数③2的指数
*规格化的二进制小数，只要不是0.0,且没有超出表示范围，小数点左边一定是1

IEEE 754规定，单精度浮点数大小为32位
其中最高1位是符号位(sign) ，随后8位是指数域(exponent)
剩下的位全部用来表示尾数(fraction)

浮点表示范围

8位指数可以表示从0_{255共256个自然数，但是只有1}254表示真正的浮点数
为了便于比较大小，浮点数的指数域采用一种类似于移码的表示方法
-126~+ 127的真正指数分别映射到1 (00000001) ~254 (11111110)
也就是说，计算出真正的指数(阶数)之后,还要加上127的偏阶为什么是127?

因此，单精度浮点数的表示范围（绝对值）是

IEEE754双精度浮点数

为了表示范围更大、精度更高的浮点数，IEEE 754提供了双精度浮点数标准,共64位
其中最高1位是符号位，随后11位是指数域，剩下的位全部用来表示尾数

此时偏阶相应变为1023 试计算双精度浮点数的表示范围

将IEEE 754单精度浮点数1 1000000 1010 0000… .转换为十进制真值

-1.01 * 2^2

IEEE 754标准后来扩充了16位半精度、128位四精度浮点数标准

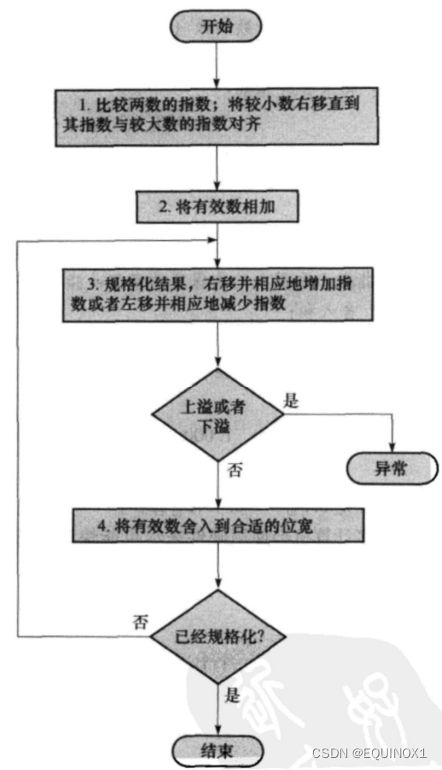
浮点加法运算的步骤

以0.5-0.4375为例，转换为二进制科学计数法
第一步，小对大:指数较小的数化为较大指数的形式
第二步，再相加:列竖式相加
第三步，规格化:将和重新规格化
第四步，舍入查:四舍五入，检查是否发生指数溢出
对单精度,指数高于+127称为上溢，低于-126称为下溢

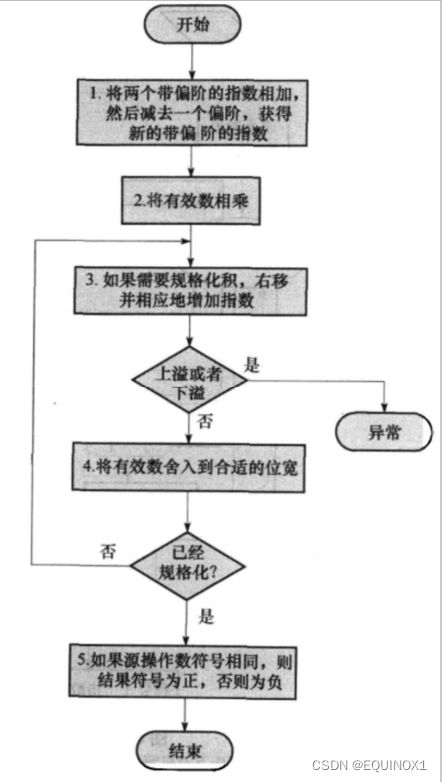
浮点乘法运算的步骤.

以0.5*(-0.4375)为例，先不考虑正负号

1.0 * 2 ^ (-1) 1.11 * 2 ^ (-2)

第一步，指数加:被乘数和乘数的指数相加
*注意，是真正指数(而不是加了偏阶的指数)相加
第二步，再相乘:列竖式相乘

第三步，规格化：将积重新规格化

第四步，舍入查：四舍五入，检查是否发生指数溢出

第五步，定符号：如果被乘数和乘数反号，则符号位为1

MIPS浮点运算指令算术运算精度

为了专门存放浮点数，MIPS体系结构增加了单独的32个单精度浮点寄存器$f0$f31,一对单精度寄存器组合成一个双精度寄存器，以偶数编号

add sub mul (不是mult) div打点加s表示单精度/d表示双精度,构成浮点运算指令
浮点比较指令有单精度c.x.s和双精度c.x.d两组
x可以取六种比较条件中的一个(eq、 neq、 It、 le、 gt、ge)
当比较条件为真时，将浮点比较结果置为1，否则置为0
随后，使用浮点比较为真跳转bclt或浮点比较为假跳转bclf指令进行条件分支

浮点数不能表示所有实数，通常只是一个近似值，舍入时需要硬件保留更多有效位
IEEE 754右边总是多保留两个额外的尾数位用于舍入，分别叫做保护位和舍入位
在正常情况下，尾数最低位(unit in the last place, ulp) 误差数目不超过0.5

即，误差都在半个ulp内

例：将2.56(10)和2.34x10 ^ 2相加

2.56 = 0.0256 * 10 ^ 2

2.56 + 2.34x10 ^ 2 = 2.3656

由于需要舍弃掉后两位，保护位为5，舍入位为6，以50为分水岭，我们进位得2.37

子字并行 矩阵乘法

在图像和音频处理中，经常出现将一组数据进行相同运算的情况

例如在一个128位的宽字中，可以拆分出16个8位数，分割进位链后同时进行运算

在这种宽字内部进行的并行操作称为子字并行，也叫数据级并行

也称为向量或SIMD

ARM的NEON多媒体指令集、x86的MMX和SSE指令集
都用于支持子字并行向量运算
2011年，英特尔使用高基向量扩展AVX扩大了寄存器宽度
用于支持高速的向量运算
作者测试，通过修改C代码使用AVX
能够将矩阵乘法示例加速4倍

*我们常用sll实现乘二的幂，但是用srl来实现除以二的幂会出现问题

复习题

1、IEEE 754浮点数分为哪三段?分别代表什么含义?

符号位 指数域 尾数

2、三个字段在单双精度中各有多长?由此得出，单双精度的偏阶分别为多少?

1 8 23 1 11 52

127 1023

3、单双精度表示真正浮点数（非0浮点数）的范围分别是多少?

1.23个0 * 2 ^ (-126) 1.23个1 * 2 ^ (127)

4、IEEE 754浮点数和十进制真值的转化要登峰造极、熟稔于心
5、浮点加法有哪四个步骤?浮点乘法有哪五个步骤?

小对大 再相加 规格化 舍入查

指数加 再相乘 规格化 舍入查 定符号

6、IEEE 754保留的额外两个尾数位分别叫什么?其运算误差不超过多少个ulp?

保护位 舍入位 0.5