动态求连续区间和+数列区间最大值（快速掌握线段树的基本性质及应用）

快速掌握线段树的基本性质及应用

前言

本文章将会站在初学者的角度，从 动态求连续区间和，还有 数列区间最大值
这两个题目讲述线段树的应用还有基本性质，此外，对于线段树我将从官方解释和自定义解释两个角度入手，帮助刚刚接触到线段树的小伙伴们更好理解线段树。

线段树的定义【学术解释】

线段树（Segment Tree）是一种用于高效处理区间查询的数据结构。它将一个数组表示为一棵二叉树，每个节点表示数组中的一个区间。

线段树的根节点表示整个数组的区间，每个叶子节点表示数组中的一个单独元素。每个非叶子节点表示一个区间，其左子节点和右子节点分别表示该区间的左半部分和右半部分。

线段树的主要操作是构建和查询。构建操作用于将给定的数组构建成线段树，查询操作用于在线段树中查找指定区间的和、最小值、最大值等。

线段树的构建过程是一个递归的过程，从根节点开始，将数组不断分割成更小的区间，直到每个叶子节点表示一个单独的元素。

线段树的查询操作也是一个递归的过程，从根节点开始，根据查询的区间与当前节点表示的区间的关系，递归地向下查询左子节点或右子节点，直到找到包含查询区间的节点或完全不相交的节点。

线段树的优势在于它可以在 O(logn) 的时间复杂度内完成各种区间查询操作，比如求和、求最小值、最大值等。因此，它在需要频繁进行区间查询的场景下非常有用，比如动态数组的区间更新和查询、区间统计等。

线段树的理解【自定义解释】

二叉树

上面的是官方的解释，下面我自己的理解，看图，线段树是个二叉树，长下面这个样子

假设存在一个 节点 u ，u 的左儿子节点 是 2 * u ，右儿子节点是 2 * u +1;
但是在算法运算过程当中，我们为了提高效率会用位运算符表示，所以左儿子表示为
u<<1 右儿子表示为 u<<1 | 1

二叉树的存储

可能有小伙伴看到二叉树是二维图形，所以需要一个二维数组去储存。其实不是这样，看图

总结出来的规律如下，看图

线段树

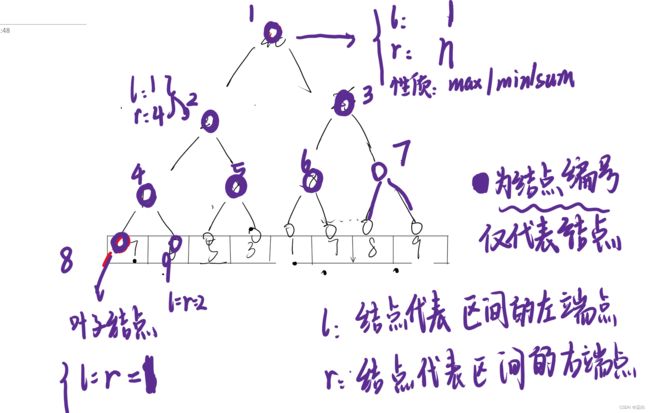
给出一个数组，我们产生它的线段树，看图

每个节点有三个性质，我们用结构体来记录这三个性质，看图

代码如下：注意数组的长度要开成 4 * N ，防止超出范围

struct Node{
    int l,r;
    int sum;
    
}tr[4*N];

sum是节点代表的性质，表示区间和，也可以换成 min max等等，这取决于题意

线段树的构建

线段树的构建过程是一个递归的过程，从根节点开始，将数组不断分割成更小的区间，直到每个叶子节点表示一个单独的元素。

我们一般将根节点设为 1 号节点
假设我们要求的是区间和，性质是sum
我们设置一个build函数，包含3个参数，根节点，区间左端点，区间右端点
具体解释可以看注释

void build(int u,int l,int r)
{
    tr[u].l=l,tr[u].r=r;//先为区间的左右端点赋值
    if(l==r){//如果左端点==右端点，说明是叶子结点
        tr[u].sum=w[l];//为也叶子节点性质赋值
        return ;
    }
    //下列为递归操作
    int mid=l+r>>1;//这里对大区间进行等分，为两个
    //子区间提供边界值
    build(u<<1,l,mid);
    build(u<<1|1,mid+1,r);
    push(u);//push 操作是在设置了叶子节点之后，需要改变上面的节点，后面会解释
}

线段树自下而上的构建特色

线段树自下而上的构建特色，也是我们为什么采用递归的手法构建线段树
先看代码

void push(int u){
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}

再看图

线段树单点的修改操作

需要一个add函数 ，参数为根节点 ， 点在数组的位置，要修改的值
代码如下

void add(int u,int x,int v){
    if(tr[u].l==tr[u].r){//当我们找到子节点时可以进行操作了
        tr[u].sum+=v;
        return ;//这里要及时停止，否则会超时
    }
    //接下来的操作与二分查找类似
    //判断 x 在区间段的左部分还是右部分，
    //进而进行递归查找，进而找到叶子节点
    int mid=tr[u].l+tr[u].r>>1;
    if(x<=mid) add(u<<1,x,v);
    else add(u<<1|1,x,v);
    push(u);//完成修改之后需要重新修改父节点以上的值
}

线段树的查询操作【这里以求区间和为例】

在这里我们设置query函数参数是根节点 ，查找区间的范围左端点，右端点
首先判断区间能否覆盖节点代表的区间，如果查询区间不能覆盖节点代表的区间，那么节点的区间和就不是查询的区间和。
注意有一个盲区，就是查询的区间必然在根节点表示的区间之内，不少小伙伴会忽略这一点
在未覆盖的情况下分情况讨论，看图

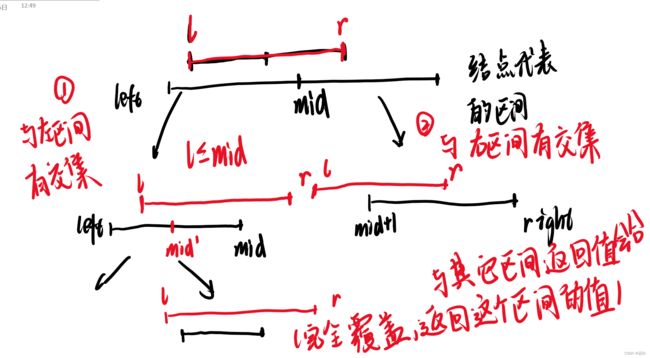
代码如下：

int query(int u,int l,int r){
    if(l<=tr[u].l&& tr[u].r<=r){
        return tr[u].sum;
    }
    int mid=tr[u].l+tr[u].r>>1;
    int sum=0;
    if(l<=mid) sum+=query(u<<1,l,r);
    if(r>=mid+1) sum+=query(u<<1|1,l,r);
    return sum;
}

例题1【动态求连续区间和】

题目描述

给定 n
个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b]
的连续和。

输入格式
第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。

第二行包含 n个整数，表示完整数列。

接下来 m 行，每行包含三个整数 k,a,b （k=0，表示求子数列[a,b]的和；k=1，表示第 a 个数加 b）。

数列从 1 开始计数。

输出格式
输出若干行数字，表示 k=0 时，对应的子数列 [a,b] 的连续和。

数据范围
1≤n≤100000
1≤m≤100000
1≤a≤b≤n
数据保证在任何时候，数列中所有元素之和均在 int 范围内。

输入样例：
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例：
11
30
35

题目分析

这里是求区间和，性质是sum

代码

#include
using namespace std;
const int N =1e5 + 7;
int n,m,w[N];
struct Node{
    int l,r;
    int sum;
    
}tr[4*N];
void push(int u){
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}

void build(int u,int l,int r)
{
    tr[u].l=l,tr[u].r=r;
    if(l==r){
        tr[u].sum=w[l];
        return ;
    }
    int mid=l+r>>1;
    build(u<<1,l,mid);
    build(u<<1|1,mid+1,r);
    push(u);
}
void add(int u,int x,int v){
    if(tr[u].l==tr[u].r){
        tr[u].sum+=v;
        return ;
    }
    int mid=tr[u].l+tr[u].r>>1;
    if(x<=mid) add(u<<1,x,v);
    else add(u<<1|1,x,v);
    push(u);
}
int query(int u,int l,int r){
    if(l<=tr[u].l&& tr[u].r<=r){
        return tr[u].sum;
    }
    int mid=tr[u].l+tr[u].r>>1;
    int sum=0;
    if(l<=mid) sum+=query(u<<1,l,r);
    if(r>=mid+1) sum+=query(u<<1|1,l,r);
    return sum;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>w[i];
    build(1,1,n);//输入完数组之后要及时构建线段树
    while(m--){
        int k,l, r;
        cin>>k>>l>>r;
        if(k==1) add(1,l,r);
        else cout<<query(1,l,r)<<endl;
    }
    return 0;
}

例题2【区间数列最大值】

题目描述

输入一串数字，给你 M个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。

输入格式
第一行两个整数 N,M 表示数字的个数和要询问的次数；

接下来一行为 N 个数；

接下来 M 行，每行都有两个整数 X,Y

输出格式
输出共 M 行，每行输出一个数。

数据范围
1≤N≤105
1≤M≤106
1≤X≤Y≤N

数列中的数字均不超过2^31−1
输入样例：
10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8
输出样例：
5
8

题目分析

这里是求最大值，性质是max

代码

#include
#include
using namespace std;
const int N = 1e5 + 7;
int n,m,w[N];
struct Node{
    int l,r;
    int m;
}tr[N*4];

void push(int u){
    tr[u].m=max(tr[u<<1].m,tr[u<<1|1].m);
}

void build(int u,int l,int r){
    tr[u].l=l,tr[u].r=r;
    if(l==r){
        tr[u].m=w[l];
        return ;
    }
    int mid=l+r>>1;
    build(u<<1,l,mid);
    build(u<<1|1,mid+1,r);
    push(u);
}

int query(int u,int l,int r){
    if(l<=tr[u].l && tr[u].r<=r){
        return tr[u].m;
    }
    int mid=tr[u].l+tr[u].r>>1;
    int sum=INT_MIN;
    if(l<=mid) sum=max(sum,query(u<<1,l,r));
    if(r>=mid+1) sum=max(sum,query(u<<1|1,l,r));
    return sum;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        scanf("%d",&w[i]);
    };
    build(1,1,n);
    int x,y;
    while(m--){
        scanf("%d %d",&x,&y);
        printf("%d\n",query(1,x,y));
    }
    return 0;
}