分治-归并排序

315. 计算右侧小于当前元素的个数

1. 题目

题目链接：315. 计算右侧小于当前元素的个数

给你一个整数数组 nums ，按要求返回一个新数组 counts 。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

示例 1：

输入：nums = [5,2,6,1]
输出：[2,1,1,0] 
解释：
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素

示例 2：

输入：nums = [-1]
输出：[0]

示例 3：

输入：nums = [-1,-1]
输出：[0,0]

提示：

• 1 <= nums.length <= 10⁵
• -10⁴ <= nums[i] <= 10⁴

⛅2. 算法原理

这题要找的是当前元素的后面，有多少个比它小的元素。

解法一：暴力枚举

固定一个原始，然后往后扫码，看看有多少个元素是小于它的，时间复杂度为O(N²)，题目的数据量较大，这个复杂度肯定会超时。

解法二：分治

如图：

由于这里是要返回一个数组，返回的数组要对应原始数组的下标，所以这里我们要找到当前元素的原始下标是多少。

这里找映射，一般采用的就是哈希表，但是如果这里有重复的元素，哈希表就失效了。我们可采取一个数组和原始的数组原始绑定

nums: [15,17,20,23,12,3]
index:[ 0, 1, 2, 3, 4,5]

3. 代码实现

class Solution {
    vector<int> ret;
    vector<int> index;
    int tmpNums[500001];
    int tmpIndex[500001];
public:
    vector<int> countSmaller(vector<int>& nums)
    {
        int n = nums.size();
        ret.resize(n);
        index.resize(n);
        for(int i=0; i<n; i++)  index[i] = i;
        mergeSort(nums, 0, n-1);
        return ret;
    }

    void mergeSort(vector<int>& nums, int left, int right)
    {
        if(left >= right)   return;
        int mid = (left + right) >> 1;
        mergeSort(nums, left, mid);
        mergeSort(nums, mid+1, right);

        int cur1 = left,
            cur2 = mid+1,
            i = 0;
        while(cur1 <= mid && cur2 <= right)
        {
            if(nums[cur1] <= nums[cur2])
            {
                tmpNums[i] = nums[cur2];
                tmpIndex[i++] = index[cur2++];    
            }
            else
            {
                ret[index[cur1]] += right - cur2 + 1;
                tmpNums[i] = nums[cur1];
                tmpIndex[i++] = index[cur1++];
            }
        }
        while(cur1 <= mid)
        {
            tmpNums[i] = nums[cur1];
            tmpIndex[i++] = index[cur1++];
        }
        while(cur2 <= right)
        {
            tmpNums[i] = nums[cur2];
            tmpIndex[i++] = index[cur2++];
        }

        for(int i=left; i<=right; i++)
        {
            nums[i] = tmpNums[i-left];
            index[i] = tmpIndex[i-left];
        }
    }
};

运行结果：

493. 翻转对

1. 题目

题目链接：493. 翻转对

给定一个数组 nums ，如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。

你需要返回给定数组中的重要翻转对的数量。

示例 1:

输入: [1,3,2,3,1]
输出: 2

示例 2:

输入: [2,4,3,5,1]
输出: 3

注意:

1. 给定数组的长度不会超过50000。
2. 输入数组中的所有数字都在32位整数的表示范围内。

⭐2. 算法原理

这题也相当于是找逆序对，只不过它要找的是小于它2倍的对数。

解法一：暴力枚举

固定一个数，依此往后枚举，统计总共有多少对，时间复杂度为O(N²)，应该会超时

解法二：分治

这里和归并排序是有一定出入的，归并排序是一比一比较的，但这里要比较的是前面的元素大于后面元素的两倍。

还是两种策略：

1. 计算当前元素后面，有多少元素的两倍小于当前元素（降序）
   利用单调性，采用同向双指针，先固定cur1，找nums[cur1] > num[cur2]*2
   
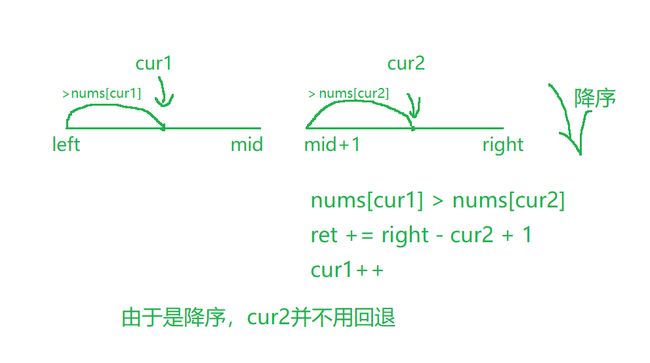
2. 计算当前元素的前面，有多少元素的两倍大于当前元素（升序）
   同理，先固定cur2，找nums[cur1] > nums[cur2]*2

3. 代码实现

class Solution {
    int tmp[50001];
public:
    int reversePairs(vector<int>& nums)
    {
        int n = nums.size();
        return mergeSort(nums,0,n-1);
    }

    int mergeSort(vector<int>& nums, int left, int right)
    {
        if(left >= right)   return 0;

        int ret = 0;
        int mid = (left+right)>>1;
        ret += mergeSort(nums, left, mid);
        ret += mergeSort(nums, mid+1, right);

        int cur1 = left,
        cur2 = mid +1,
        i = left;
        while(cur2 <= right)
        {
            while(cur1 <= mid && nums[cur2] >= nums[cur1]/2.0)   cur1++;
            if(cur1 > mid)  break;
            ret += mid - cur1 + 1;
            cur2++; 
        }
        //合并
        cur1 = left,
        cur2 = mid+1,
        i = left;
        while(cur1 <= mid && cur2 <= right)
            tmp[i++] = nums[cur1] <= nums[cur2]?nums[cur1++]:nums[cur2++];            
        while(cur1 <= mid)  tmp[i++] = nums[cur1++];
        while(cur2 <= right)    tmp[i++] = nums[cur2++];

        for(int i=left; i<=right; i++)  nums[i] = tmp[i];
        return ret;
    }
};

运行结果：