c语言-归并排序

       

目录

1、归并排序基本思想

2、归并排序的实现（递归法）

2.1 代码实现递归法归并排序 

3、归并排序的实现（非递归法）

3.1 修正边界问题

 3.2 代码实现非递归法归并排序 

结语： 

---

前言：

        归并排序是一种把数组排成有序数组的分治算法，其逻辑和归并操作是一样的，就是把两个子序列合并成一个子序列，只不过归并排序是把两个有序的子序列合并成一个有序的子序列，最后完成对数组的排序。

1、归并排序基本思想

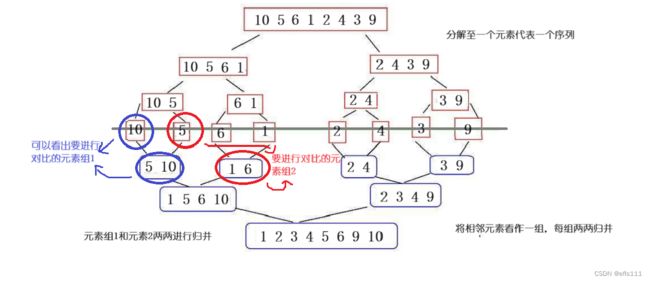
        归并排序就是把一个数组看成是由两个子序列构成，这两个子序列再继续细分，是由四个子序列构成，四个子序列又分成由八个子序列构成...如此细分下去直到一个元素代表一个序列。这样就能够将两个子序列合并成一个序列，因为此时一个序列代表一个元素，可以直接进行元素的比较，从而构成一个新的含两个元素的有序序列。

2、归并排序的实现（递归法）

         首先把数组分成两个左右区间（既序列），然后这两个左右区间再进行分区间。

        总逻辑图：

        可以从上图中看到，对一个数组不断进行分解，直到分解至最后一个元素就进行归并，该结构类似二叉树的递归结构，从递归的思想出发，也就是当递归到最后一个元素的时候，则无需再递归，递归函数逐渐向上”回收“，并且完成排序。       

---

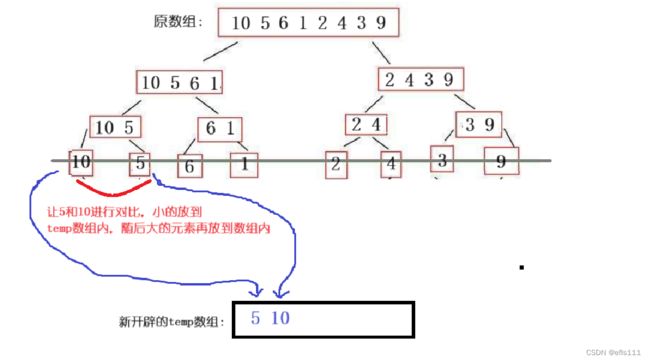
        但是如果在原数组内进行分解和归并等操作则过于复杂，因此动态开辟一个新的数组temp，让相邻元素组进行归并的时候都在数组temp上完成，最后再把新数组temp上的数据用memcpy拷贝到原数组上覆盖原先的元素的顺序，达到对原数组排序的效果。

---

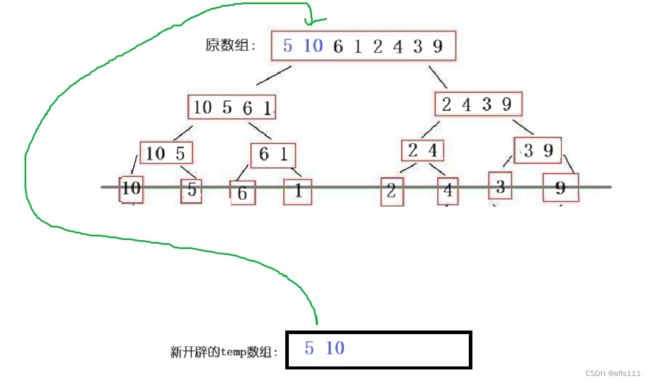
        然后把数组temp中元素拷贝到原数组内，这样原数组的元素顺序就得到了改变。 

---

        当然以上只是一部分的操作，整体逻辑与上相同，并且重复以上操作。

        最后一步就是对1 5 6 10和2 3 4 9这两组进行归并，得到的序列就是最终的有序序列。

---

        不过在此要还要注意拷贝到temp数组时，要拷贝到对应的位置上。

2.1 代码实现递归法归并排序 

        代码如下：

#include
#include
#include

void _MergeSort(int* a, int left, int right, int* temp)//归并排序
{
	if (left == right)//left==right说明递归至只有一个元素，开始向上“收回”
		return;
	int mid = (left + right) / 2;//按照mid让数组分成两个区间

	//递归函数
	_MergeSort(a, left, mid, temp);
	_MergeSort(a, mid + 1, right, temp);

	//begin1表示要进行归并的第一组元素的第一个元素，end1表示该组元素的最后一个元素
	//begin2表示要进行归并的第二组元素的第一个元素，end2表示该组元素的最后一个元素
	//begin1、end1和begin2、end2的作用就是让元素组两两进行归并
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;

	int i = left;//i的值temp数组的下标
	while (begin1 <= end1 && begin2 <= end2)//归并操作
	{
		if (a[begin1] > a[begin2])//小的元素先放到temp数组中
			temp[i++] = a[begin2++];
		else//其他情况则放在后面
			temp[i++] = a[begin1++];
	}

	//走到这里表示有一个元素组为空，则直接把另一个元素组移到temp数组中即可
	while (begin1 <= end1)
	{
		temp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		temp[i++] = a[begin2++];
	}
	//最后从temp数组中拷贝至原数组中要严格按照位置拷贝，left表示当前归并的位置
	memcpy(a + left, temp + left, sizeof(int) * (right - left + 1));
}
void MergeSort(int* a, int n)//归并排序
{
	int* temp = (int*)malloc(sizeof(int) * (n + 1));//开辟新数组
	if (temp == NULL)
	{
		perror("malloc");
		return;
	}
	_MergeSort(a, 0, n, temp);
	free(temp);
}

void PrintArr(int* a, int n)//打印数组
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

void Test_MergeSort()//归并排序
{
	int arr[] = { 10,5,6,1,2,4,3,9 };
	int sz = sizeof(arr) / sizeof(int);
	PrintArr(arr, sz);
	MergeSort(arr, sz - 1);
	PrintArr(arr, sz);
}

int main()
{
	Test_MergeSort();
	return 0;
}

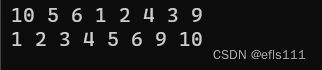
        运行结果：

        从结果看出递归法可以完成归并排序。 

3、归并排序的实现（非递归法）

        非递归方法思路图如下：

        从上图可以看出，非递归法与递归法的区别：只不过是把层层递归至只剩一个元素一组的思想换成了一开始就从一个元素一组往后不断增加每组的元素个数。其中，要进行归并的元素组1的第一个元素依然是begin1，最后一个元素是end1。元素组2的第一个元素依然是begin2，end2。

        但是非递归法再面对数组有九个元素的时候，就不能像以上一样每组元素完整的对比了。

3.1 修正边界问题

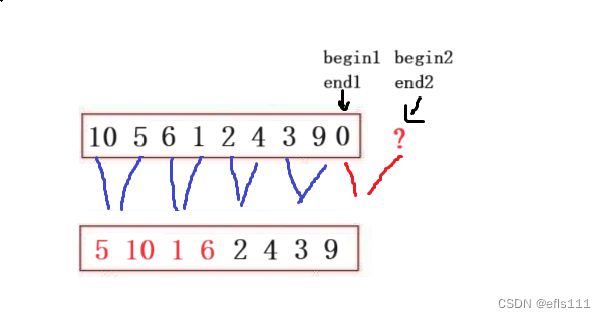
        不过非递归法再处理数组元素个数不为2的幂次方时，比如对要排序的数组的元素个数为9个时，会出现越界问题。

        这里begin2和end2的值明显是超出了数组的最后一个元素的下标值，因此如果访问begin2、end2会发生越界。所以这里采取让begin2的值大于end2的值，让他们成为一个不存在的区间，因此在代码中就不会对他们进行访问了（结合上述代码中归并操作while循环条件）。

---

        从上文的非递归思路图来看，当数组中有8个元素，则在gap=4的时候就完成了对数组的排序，也可以理解为当gap=8时结束排序操作。但是若数组中有9个元素，则gap=8时并不会结束排序操作，而是会再进行一轮排序，而该轮排序就是对第9个元素进行归并的关键一轮排序，所以在gap=8之前我们要让第9个元素和与他对比的元素组不参与进来，等到gap=8时，在进行对end2的修正从而间接的让第9个元素进行归并。

 3.2 代码实现非递归法归并排序 

        代码如下：

#define _CRT_SECURE_NO_WARNINGS 1

#define _CRT_SECURE_NO_WARNINGS 1

#include
#include
#include

void _MergeSortNon(int* a, int n, int* temp)//归并排序(非递归法)
{
	int gap = 1;//从一个元素一个元素组开始
	while (gap < n)//gap>=n时说明排序完成
	{
		int j = 0;//temp数组下标
		for (int i = 0; i < n; i += 2 * gap)//元素组1和下一个元素组1直接的间隔是2*gap
		{
			//设置元素组1和元素组2的第一个元素和最后一个元素下标
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//修正
			if (end1 >= n)//当end1超出范围则表示begin2和end2也超出范围
			{
				end1 = n - 1;//修正end1让其等于begin1，表示该元素在数组中没有变动

				//让元素组2的begin2>end2，目的不让其进入下面的while循环，也就不会发生越界了
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >= n)//目的也是不然元素组2进入while循环
			{
				begin2 = n;
				end2 = n - 1;
			}
			else if (end2 >= n)//来到这局代码，说明begin2 a[begin2])
					temp[j++] = a[begin2++];
				else
					temp[j++] = a[begin1++];
			}
			while (begin1 <= end1)
			{
				temp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				temp[j++] = a[begin2++];
			}
		}
		memcpy(a, temp, sizeof(int) * n);//最后拷贝数组即可
		gap *= 2;
	}
}
void MergeSortNon(int* a, int n)//归并排序(非递归法)
{
	int* temp = (int*)malloc(sizeof(int) * n);
	if (temp == NULL)
	{
		perror("malloc");
		return;
	}
	_MergeSortNon(a, n, temp);
	free(temp);
}

void PrintArr(int* a, int n)//打印数组
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

void Test_MergeSortNon()//归并排序(非递归法)
{
	int arr[] = { 10,5,6,1,2,4,3,9,0, };
	int sz = sizeof(arr) / sizeof(int);
	PrintArr(arr, sz);
	MergeSortNon(arr, sz);
	PrintArr(arr, sz);
}

int main()
{
	Test_MergeSortNon();
	return 0;
}

        运行结果：

        从结果中可以看出非递归法也能实现归并排序。

结语： 

         以上就是关于归并排序的介绍，归并排序的递归法和非递归法主要还是以归并操作的逻辑为主。只是对于归并排序的非递归方法而言，其逻辑确实有些复杂，但是只要理解了边界修正的问题还是能够很好的理解此方法的，最后希望本文可以给你带来更多的收获，如果本文对你起到了帮助，希望可以动动小指头帮忙点赞+关注+收藏！如果有遗漏或者有误的地方欢迎大家在评论区补充~！！谢谢大家！！(～￣▽￣)～