【解题报告】《九日集训》(第八天)
语言:C++
图书馆闭馆了,那个中等题还没做出来
文章目录
- 832. 翻转图像
- 867. 转置矩阵
- 566. 重塑矩阵
- 2022. 将一维数组转变成二维数组
- 1260. 二维网格迁移
- 661. 图片平滑器
-
-
-
- [1314. 矩阵区域和](https://leetcode-cn.com/problems/matrix-block-sum/)
-
-
- 1030. 距离顺序排列矩阵单元格
832. 翻转图像
832. 翻转图像
给定一个二进制矩阵 A,我们想先水平翻转图像,然后反转图像并返回结果。
水平翻转图片就是将图片的每一行都进行翻转,即逆序。例如,水平翻转 [1, 1, 0] 的结果是 [0, 1, 1]。
反转图片的意思是图片中的 0 全部被 1 替换, 1 全部被 0 替换。例如,反转 [0, 1, 1] 的结果是 [1, 0, 0]。
示例 1:
输入:[[1,1,0],[1,0,1],[0,0,0]]
输出:[[1,0,0],[0,1,0],[1,1,1]]
解释:首先翻转每一行: [[0,1,1],[1,0,1],[0,0,0]];
然后反转图片: [[1,0,0],[0,1,0],[1,1,1]]
写了两个函数swap(交换数值)和flip(翻转)
class Solution
{
public:
void Swap(int& a, int& b)
{
int tmp = a;
a = b;
b = tmp;
}
void flip(int& a)
{
if (a)
a = 0;
else
a = 1;
}
vector<vector<int>> flipAndInvertImage(vector<vector<int>>& image)
{
int i = 0;
for (auto n : image)
{
int left = 0;
int right = n.size() - 1;
while (left < right)
{
Swap(n[left], n[right]);
flip(n[left++]);
flip(n[right--]);
}
if (n.size() & 1)
{
flip(n[n.size() / 2]);
}
image[i++] = n;
}
return image;
}
};
从这个题发现auto n:image,就是单纯的把image的数组复制一份出来,在n上修改不影响image的值
867. 转置矩阵
867. 转置矩阵
给你一个二维整数数组 matrix, 返回 matrix 的 转置矩阵 。
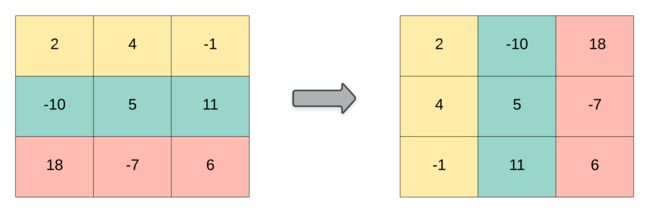
矩阵的 转置 是指将矩阵的主对角线翻转,交换矩阵的行索引与列索引。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[1,4,7],[2,5,8],[3,6,9]]
新建数组保存
class Solution
{
public:
vector<vector<int>> transpose(vector<vector<int>>& matrix)
{
vector<vector<int>>arr(matrix[0].size(), vector<int>(matrix.size()));
for (int i = 0; i < matrix.size(); ++i)
{
for (int j = 0; j < matrix[i].size(); ++j)
{
arr[j][i] = matrix[i][j];
}
}
return arr;
}
};
566. 重塑矩阵
566. 重塑矩阵
在 MATLAB 中,有一个非常有用的函数 reshape ,它可以将一个 m x n 矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。
给你一个由二维数组 mat 表示的 m x n 矩阵,以及两个正整数 r 和 c ,分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。
如果具有给定参数的 reshape 操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
示例 1:
遍历保存,先判断是否合法
class Solution
{
public:
vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c)
{
if (r * c != mat.size() * mat[0].size())
return mat;
vector<vector<int>>arr(r, vector<int>(c));
int i = 0;
int j = 0;
for (auto n : mat)
{
for (auto m : n)
{
arr[i][j++] = m;
if (j == c)
{
j = 0;
i++;
}
}
}
return arr;
}
};
2022. 将一维数组转变成二维数组
2022. 将一维数组转变成二维数组
给你一个下标从 0 开始的一维整数数组 original 和两个整数 m 和 n 。你需要使用 original 中 所有 元素创建一个 m 行 n 列的二维数组。
original 中下标从 0 到 n - 1 (都 包含 )的元素构成二维数组的第一行,下标从 n 到 2 * n - 1 (都 包含 )的元素构成二维数组的第二行,依此类推。
请你根据上述过程返回一个 m x n 的二维数组。如果无法构成这样的二维数组,请你返回一个空的二维数组。
示例 1:
输入:original = [1,2,3,4], m = 2, n = 2
输出:[[1,2],[3,4]]
解释:
构造出的二维数组应该包含 2 行 2 列。
original 中第一个 n=2 的部分为 [1,2] ,构成二维数组的第一行。
original 中第二个 n=2 的部分为 [3,4] ,构成二维数组的第二行。
新建数组保存
class Solution
{
public:
vector<vector<int>> construct2DArray(vector<int>& original, int m, int n)
{
vector<vector<int>>arr(m, vector<int>(n));
if (m * n != original.size())
{
arr.clear();
return arr;
}
int i = 0, j = 0;
for (auto k : original)
{
arr[i][j] = k;
if (++j == n)
{
j = 0;
++i;
}
}
return arr;
}
};
优化了一点
class Solution
{
public:
vector<vector<int>> construct2DArray(vector<int>& original, int m, int n)
{
if (m * n != original.size())
{
return vector<vector<int>>{};
}
vector<vector<int>>arr(m, vector<int>(n));
int i = 0, j = 0;
for (auto k : original)
{
arr[i][j] = k;
if (++j == n)
{
j = 0;
++i;
}
}
return arr;
}
};
1260. 二维网格迁移
1260. 二维网格迁移
给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。
每次「迁移」操作将会引发下述活动:
- 位于
grid[i][j]的元素将会移动到grid[i][j + 1]。 - 位于
grid[i][n - 1]的元素将会移动到grid[i + 1][0]。 - 位于
grid[m - 1][n - 1]的元素将会移动到grid[0][0]。
请你返回 k 次迁移操作后最终得到的 二维网格。
示例 1:
输入:grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[9,1,2],[3,4,5],[6,7,8]]
朋友们,这道题做的太拉了
图书馆闭馆了,没时间优化
class Solution
{
public:
vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k)
{
int i = 0;
int lenn = grid[0].size();
int tmp = k;
vector<vector<int>>arr;
while (tmp)
{
i = 0;
arr.clear();
for (auto n : grid)
{
for (int j = 0; j < lenn; j++)
{
n[(j + 1) % lenn] = grid[i][j];
if (i > 0 && j == lenn - 1)
{
n[0] = grid[i - 1][j];
}
}
arr.push_back(n);
arr[0][0] = grid[grid.size() - 1][n.size() - 1];
++i;
}
grid = arr;
tmp--;
}
return grid;
}
};
661. 图片平滑器
661. 图片平滑器
包含整数的二维矩阵 M 表示一个图片的灰度。你需要设计一个平滑器来让每一个单元的灰度成为平均灰度 (向下舍入) ,平均灰度的计算是周围的8个单元和它本身的值求平均,如果周围的单元格不足八个,则尽可能多的利用它们。
示例 1:
输入:
[[1,1,1],
[1,0,1],
[1,1,1]]
输出:
[[0, 0, 0],
[0, 0, 0],
[0, 0, 0]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0
对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0
对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0
不停的用 if…else… 判断 i、j 条件的合法性
class Solution
{
public:
vector<vector<int>> imageSmoother(vector<vector<int>>& img)
{
vector<vector<int>>arr(img.size(), vector<int>(img[0].size(), 1));
for (int i = 0; i < img.size(); ++i)
{
for (int j = 0; j < img[i].size(); ++j)
{
int sum = 0;
int tmp = 0;
sum += img[i][j];
tmp++;
if (i - 1 >= 0)
{
sum += img[i - 1][j];
tmp++;
}
if (j - 1 >= 0)
{
sum += img[i][j - 1];
tmp++;
}
if (i + 1 < img.size())
{
sum += img[i + 1][j];
tmp++;
}
if (j + 1 < img[i].size())
{
sum += img[i][j + 1];
tmp++;
}
if (i - 1 >= 0 && j - 1 >= 0)
{
sum += img[i - 1][j - 1];
tmp++;
}
if (i - 1 >= 0 && j + 1 < img[i].size())
{
sum += img[i - 1][j + 1];
tmp++;
}
if (i + 1 < img.size() && j - 1 >= 0)
{
sum += img[i + 1][j - 1];
tmp++;
}
if (i + 1 < img.size() && j + 1 < img[i].size())
{
sum += img[i + 1][j + 1];
tmp++;
}
arr[i][j] = sum / tmp;
}
}
return arr;
}
};
1314. 矩阵区域和
难度中等119
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
i - k <= r <= i + k,j - k <= c <= j + k且(r, c)在矩阵内。
示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[12,21,16],[27,45,33],[24,39,28]]
1030. 距离顺序排列矩阵单元格
1030. 距离顺序排列矩阵单元格
给出 R 行 C 列的矩阵,其中的单元格的整数坐标为 (r, c),满足 0 <= r < R 且 0 <= c < C。
另外,我们在该矩阵中给出了一个坐标为 (r0, c0) 的单元格。
返回矩阵中的所有单元格的坐标,并按到 (r0, c0) 的距离从最小到最大的顺序排,其中,两单元格(r1, c1) 和 (r2, c2) 之间的距离是曼哈顿距离,|r1 - r2| + |c1 - c2|。(你可以按任何满足此条件的顺序返回答案。)
示例 1:
输入:R = 1, C = 2, r0 = 0, c0 = 0
输出:[[0,0],[0,1]]
解释:从 (r0, c0) 到其他单元格的距离为:[0,1]
学会了如何在class中自定义sort
这个题感觉用C的qsort写会更容易点
class Solution
{
public:
vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter)
{
vector<vector<int>>arr;
for (int i = 0; i < rows; ++i)
{
for (int j = 0; j < cols; ++j)
{
arr.push_back({ i,j });
}
}
sort(arr.begin(), arr.end(), [=](vector<int>& a, vector<int>& b) {
return abs(a[0] - rCenter) + abs(a[1] - cCenter) < abs(b[0] - rCenter) + abs(b[1] - cCenter);
});
return arr;
}
};