数据结构--栈与队列
文章目录
- 0.PTA得分截图
- 1.本周学习总结(0-5分)
-
- 1.1 栈
-
- 1.1.1 关于栈的初步介绍
- 1.1.2 顺序栈的结构及其操作函数
- 1.1.3 顺序栈中的共享栈结构及其操作函数
- 1.1.4 链栈的结构及其操作函数
- 1.2 栈的应用
-
- 1.2.1 表达式问题
- 1.3 队列
-
- 1.3.1 队列的一些基础要素:
- 1.3.2 顺序队列的结构及其操作函数:
- 1.3.3 环形队列的结构及其操作函数:
- 1.3.4 链队列的结构及其操作函数:
- 1.3.5 队列的具体应用(有代码要求):
-
- 1.3.5.1那么不妨先思考一下,队列能做些什么呢?
- 1.3.5.2 部分相关代码:
- 2.PTA实验作业(4分)
-
- 2.1 符号配对
-
- 2.1.1 解题思路及伪代码
- 2.1.2 总结解题所用的知识点
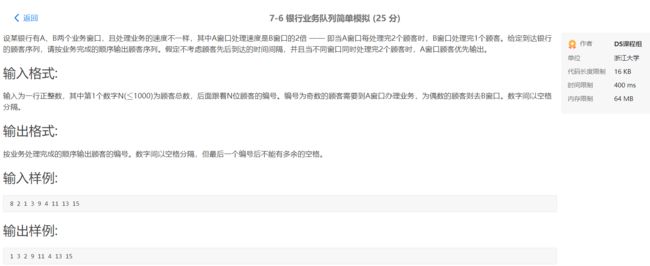
- 2.2 银行业务队列简单模拟
-
- 2.2.1 解题思路及伪代码
- 2.2.2 总结解题所用的知识点
- 3.阅读代码(0--1分)
-
- 3.1 题目及解题代码
- 3.2 该题的设计思路及伪代码
- 3.3 分析该题目解题优势及难点。
- 4.通过Debug得到的一些感想。
| 这个作业属于哪个班级 | C语言–网络2011/2012 |
|---|---|
| 这个作业的地址 | DS博客作业02–栈和队列 |
| 这个作业的目标 | 学习栈和队列的结构设计及运算操作 |
| 姓名 | 骆锟宏 |
0.PTA得分截图
1.本周学习总结(0-5分)
1.1 栈
the photo of stack is followed:

*
1.1.1 关于栈的初步介绍
- 栈在C++的STL库中有专门的容器,仅需要
#include就可以使用,不过值得一提的是,C++中的
stack容器的底层结构是链栈。 - 中的常用成员函数有如下几种:
- top():返回栈顶的元素;
- push():对某一数据执行进栈操作;
- pop():讲栈顶元素出栈;
- empty():判断当前栈是否为空,如果为空返回true;
- size():返回当前栈中所含有的数据的数目;
- 栈这种数据结构具有两个特性:
<先入后出> <随进随出>- 所以基于栈的这两个特性,我们可以得到一些基本性质:对于给定输入顺序的一组数据
我们可以根据他的第一个输出的元素来判断当前栈中有那些元素,以及可以判断出将来可能的
栈的输出组合。
- 所以基于栈的这两个特性,我们可以得到一些基本性质:对于给定输入顺序的一组数据
- 栈是线性结构,所以他同样拥有两种存储结构,一种是顺序存储结构,一种是链式存储结构;
基于这两种存储结构也就会引申出我们下面要讲的两种栈的类型:顺序栈和链栈。 - 栈适用于解决递归问题,适用于解决递归问题,函数递归调用的实现,
本身数据结构的基础就是递归栈。
1.1.2 顺序栈的结构及其操作函数
- 顺序栈的结构定义:
typedef int ElementType;
typedef int Position;
struct SNode
{
ElementType* Data;
Position Top;
int MaxSize;
};
typedef struct SNode* SQStack;
- 顺序栈初始化栈的代码:
- 当然这里也有另类堆栈的办法,就是令
top = 0;
这会相应地影响到栈的其他基础操作的具体实现。
- 当然这里也有另类堆栈的办法,就是令
void CreateSQStack(SQStack& S, int MaxSize)
{
S = new struct SNode;
S->Data = new ElementType;
S->Top = -1;
S->MaxSize = MaxSize;
}
- 顺序栈的进栈操作的代码:
- 如果是另类栈的话,栈满的判断条件就要变成
S->Top == S->MaxSize; - 同时入栈的操作会变成
S->Data[S->Top++] = X;;
- 如果是另类栈的话,栈满的判断条件就要变成
bool Push(SQStack S, ElementType X)//顺序堆栈的入栈操作
{
//入栈操作要先判断是否栈满
if (S->Top == S->MaxSize-1)//栈满了
{
printf("SQStack Full\n");
return false;
}
//正常入栈
S->Data[++S->Top] = X;
return true;
}
- 顺序栈的出栈操作(出栈包含了判断栈是否为空的代码)的代码:
- 如果是另类建栈的话,那判断栈是否为空的条件就会变成
S->Top == 0; - 同样的出栈的操作也就会变成
return S->Data[--S->Top]; - 以及还有一点是,虽然是出栈,但是如果没有进行后续入栈操作对现出栈位置进行数据覆盖的话,其实出
栈的元素只是逻辑上被删除了,但是实际上并没有被删除,准确给出下标地址的话,依然可用被输出。
- 如果是另类建栈的话,那判断栈是否为空的条件就会变成
ElementType Pop(SQStack S)//顺序栈的出栈操作
{
/*先判断栈是否为空*/
if (S->Top == -1)
{
printf("SQStack Empty\n");
return ERROR;
}
//正常出栈
return S->Data[S->Top--];
}
-
关于获取当前栈的元素个数:
- 如果是正常建栈的话,那就是
return S->Top+1; - 如果是另类建栈的话,那就是
return S->Top;
- 如果是正常建栈的话,那就是
-
准确来说还有一个销毁栈的操作,对于顺序栈而言,一般直接delete栈就行。
1.1.3 顺序栈中的共享栈结构及其操作函数
- 共享栈的结构定义:
typedef int ElementType;
typedef int Position;
struct SNode {
ElementType* Data;
Position Top1, Top2;
int MaxSize;
};
typedef struct SNode* SharedStack;
- 共享栈的创建:
void CreateSharedStack(SharedStack& S,int MaxSize)//创建共享栈
{
S = new struct SNode;
S->Data = new ElementType;
S->Top1 = -1;
S->Top2 = MaxSize;
}
- 共享栈的入栈操作:
- 要特别注意的是另外一个方向的栈,这个比较反常思维的栈的操作要尤其注意。
bool Push(SharedStack S, ElementType X, int Tag)//共享栈的进栈操作
{
/*进栈要考虑栈是否满*/
if (S->Top1 + 1 == S->Top2)
{
printf("SharedStack Full\n");
return false;
}
if (Tag == 1)
{
S->Data[++S->Top1] = X;
return true;
}
else
{
S->Data[--S->Top2] = X;
return true;
}
}
- 共享栈的出栈操作:
- 仍然要注意的是,共享站另外一边的栈思维有点反常态所以要特别注意。
- 其次是出栈的时候我们需要判断栈是否为空,而共享站两边的栈栈空条件是不一样的,所以要分开来判断。
- 以及还有一点是,虽然是出栈,但是如果没有进行后续入栈操作对现出栈位置进行数据覆盖的话,其实出
栈的元素只是逻辑上被删除了,但是实际上并没有被删除,准确给出下标地址的话,依然可用被输出。
ElementType Pop(SharedStack S, int Tag)//共享栈的出栈操作
{
/*共享栈要分开考虑栈是否为空的情况*/
if (Tag == 1)
{
/*栈空判断*/
if (S->Top1 == -1)
{
printf("SharedStack %d Empty\n", Tag);
return ERROR;
}
return S->Data[S->Top1--];
}
else
{
/*栈空判断*/
if (S->Top2 == S->MaxSize)
{
printf("SharedStack %d Empty\n", Tag);
return ERROR;
}
return S->Data[S->Top2++];
}
}
-
共享栈的取栈顶操作:
- 对左栈来说,取栈顶元素就是
S->Data[S->Top1]; - 对右栈来说,取栈顶元素就是
S->Data[S->Top2];
- 对左栈来说,取栈顶元素就是
-
准确来说还有一个销毁栈的操作,对于顺序栈而言,一般直接delete栈就行。
1.1.4 链栈的结构及其操作函数
-
链栈的结构基础其实仍然是链表,出于栈只能在一端进行入栈和出栈的操作的考虑,所以一般选择
链表的第一个结点处为栈顶,而取链表为栈底,又由于栈的入栈和出栈操作本质上就是链表的插入和
删除操作,所以保留表头方便再头处(也就是栈顶)进行入栈和出栈操作,总之,可以把链栈看成一
个带有头指针的只在头处进行插入删除操作的链表来使用就行。 -
链栈的结构基本定义:(本质上还是链表的定义)
typedef int Elmetype;
struct SNode
{
Elmetype data;
struct SNode* next;
};
typedef struct SNode* LinkStack;
- 链栈的初始化函数:
- 此处添加了一个数据载入的过程,可以让链栈的初始化拥有初始数据而非空。
void CreateLinkStack(LinkStack& S,int n)
{
S = new SNode;
S->next = NULL;
for (int i = 0; i < n; i++)
{
LinkStack NewS = new SNode;
/*数据载入*/
cin >> NewS->data;
/*头插法插入新数据*/
NewS->next = S->next;
S->next = NewS;
}
}
- 链栈的进栈操作:
- 值得注意的一点是,链栈的进栈不需要考虑栈是否栈满的问题。
void Push(LinkStack& S, Elmetype X)
{
LinkStack NewS = new SNode;
/*数据载入*/
NewS->data = X;
/*头插法插入新数据*/
NewS->next = S->next;
S->next = NewS;
}
- 链栈的出栈操作:
- 出栈前一定要判断栈是否为空,如果栈空则无法出栈;
- 相对于数组栈出栈时并非真的将源数据删除,链栈的删除是的的确确的把链栈中
出栈的结点,在物理意义上完全删除了;
bool Pop(LinkStack& S, Elmetype& e)
{
/*首先要判断栈顶是否为空*/
if (S->next == NULL)
{
return false;
}
e = S->next->data;
LinkStack delSNode = S->next;
S->next = delSNode->next;
delete delSNode;
return true;
}
-
链栈的取栈顶元素操作:
- 本质上来说就是取
S->next->Data;
- 本质上来说就是取
-
链栈的销毁操作:
- 本质上和链表的销毁是一样的,需要一个结点一个结点地销毁。
void DestoryLinkStack(LinkStack& S)
{
LinkStack delS = S;
while (S != NULL)
{
S = S->next;
delete delS;
delS = S;
}
}
1.2 栈的应用
- 据目前有学习过的部分来说,栈有这几个方面的应用:
- 一个是表达式转换(常用的是将中缀表达式转化为后缀表达式)
- 一个是表达式求值 (本质上仍然是先将中缀表达式转化为后缀表达式,后缀表达式的求值就很简单了)
- 还有一个是符号的配对,详细的思路和代码可以参考下文部分2的例题
- 当然栈还可以实现将十进制数转化成n进制数。(来自课堂派测试题)
- 借用栈结构可以实现深度搜索(迷宫问题)
1.2.1 表达式问题
- 表达式转换(将中缀表达式转换为后缀表达式)
- 先规定一下前提:目前给出的表达式每个操作数都是一位整数,
且需要考虑的运算符号只有'+' '-' '*' '/' '(' ')'这六个符号。 - 暂时不考虑操作数带有 小数,带有 负数,带有多位整数这类情况的表达式转换。
- 先规定一下前提:目前给出的表达式每个操作数都是一位整数,
- 解题思路:
- 遍历一个给定的正确的表达式
- 当遇到数字的时候,我们让数字直接输出,或者直接存储到一个字符串中之类的;
- 当栈空或者当前要进栈的运算符号比栈顶的运算符号优先级更大的时候,就让运算符进入运算符栈;
- 当遇到当前要进栈的运算符号比栈顶的运算符号优先级更小或者相等的时候,就让栈中的运算符出栈直到出到;
栈中的运算符比当前要入栈的运算符优先级更大或者栈空的时候,再让现在的运算符入栈; - 当表达式遍历结束而栈中还有符号的时候,就让栈中所有的运算符输出直到栈空;
- 对’(‘和’)‘的处理,当当下要进栈的时候,’(‘直接进栈,视为优先级最大,而当其处于栈顶时,
优先级将降为最低,任何运算符遇到它都入栈,直到当前要入栈的运算符时是’)‘时,再把’('上的所有
运算符全部输出即可。
1.3 队列
the photo of queue is followed:

1.3.1 队列的一些基础要素:
- 队列是只允许在一端进行插入(俗称队尾),然后在另一端进行删除(俗称队尾)的线性表,队列具有先入先出的特性。
- C++中也带有队列的已经实现好了的类,只需要加上
#include便可以使用了。 - 下面是常用到的一些内联函数的介绍:
- front():返回 queue 中第一个元素的引用。如果 queue 是常量,就返回一个常引用;如果 queue 为空,返回值是未定义的。
- back():返回 queue 中最后一个元素的引用。如果 queue 是常量,就返回一个常引用;如果 queue 为空,返回值是未定义的。
- pop():删除 queue 中的第一个元素。
- push():在 queue 的尾部添加一个元素的副本。
- size():返回 queue 中元素的个数。
- empty():如果 queue 中没有元素的话,返回 true。
- 当然作为线性表,队列同样有两种存储结构一种是顺序存储结构,另外一种是链式存储结构,而这两种就分别对应了两种
队列类型的具体实现,也就是下面要讲到的顺序队列和链队列。
1.3.2 顺序队列的结构及其操作函数:
- 顺序队列的结构基础是数组,由此我们给出顺序队列的结构定义:
typedef int ElemType;
#define MaxSize 100// 100只是一个例子具体情况视题目而定。
typedef struct
{
ElemType data[MaxSize];
int front, rear; //队首和队尾指针
}Queue;
typedef Queue* SqQueue;
- 当有了一个结构后,首先我们考虑对它进行初始化:
void CreatSqQueue(SqQueue& Que)
{
Que = new Queue;
Que->front = Que->rear = 0;
//初始化的状态是队空的状态
//一般我们默认让front代表队头的位置,让rear代表队尾的下一个位置
}
- 初始化后考虑对空队列加入元素,也就是入队:
bool EnQueue(SqQueue& Q, Elmetype e)//加入队列
{
/*要先判断是否队满*/
if (Q->rear == Maxsize)
{
return false;
}
Q->data[Q->rear++] = e;
return true;
}
- 同样的,有入队也就会有出队,不过出队前要先判断队列是否为空,空队莫得出队:
bool QueueEmpty(SqQueue& Q)//队列是否为空
{
if (Q->front == Q->rear)
{
return true;
}
return false;
}
- 有了判断队列是否为空的函数就可以直接开始操作出队啦:
bool DeQueue(SqQueue& Q, Elmetype& e)//出队列
{
if (QueueEmpty(Q))
{
return false;
}
e = Q->data[Q->front++];
return true;
}
-
有始有终,使用完了后,得将队列销毁,此处由于结构比较简单可以直接
delete。 -
在这里不妨思考一个问题,刚才顺序队列中,当我们出队的时候,当下队头前的空间实际是可以使用的
但是当前的数据结构却不允许我们使用前面的空间,试想当数据量十分庞大的时候,使用这样的数据结构岂
不是会浪费很大的空间?那有没有什么办法能够利用到前面的的空间呢? -
———把数组首尾连接起来,变成一个环形,你会发现就能解决这样的问题,于是新的结构营运而生,它便是环形队列!
1.3.3 环形队列的结构及其操作函数:
- 先来看看环形队列长什么样子趴:
typedef int ElementType;
typedef int Position;
struct QNode {
ElementType* Data; /* 存储元素的数组 */
Position Front; /* 队列的头指针 */
Position Rear; /* 队列的尾指针 */
int MaxSize; /* 队列最大容量 */
};
typedef struct QNode* RingQueue;
- 同样的,知道它的结构之后,我们就要对其初始化:
- 从初始化的状态我们可以知道,
Q->Front = Q->Rear = 0;这便是循环队列为空的条件。 - 而且我们还可以知道一般来说,我们默认让front代表队头的位置,让rear代表队尾的下一个位置
- 从初始化的状态我们可以知道,
void CreateRingQueue(RingQueue& Q,int MaxSize)
{
Q = new struct QNode;
Q->Data = new ElementType[MaxSize];
Q->Front = Q->Rear = 0;
Q->MaxSize = MaxSize;
}
- 同理可以给出环形队列的入队函数:
bool EnQueue(RingQueue& Q, ElementType X)
{
if ((Q->Rear+1)%Q->MaxSize == Q->Front)//Queue Full
{
return false;
}
Q->Data[Q->Rear] = X;
Q->Rear = (Q->Rear + 1) % Q->MaxSize;
return true;
}
- 同理可以给出环形队列的出队函数:
bool DeQueue(RingQueue& Q, ElementType e)
{
if (Q->Front == Q->Rear)//Queue Empty
{
return false;
}
e = Q->Data[Q->Front];
Q->Front = (Q->Front + 1) % Q->MaxSize;
return true;
}
- 判断队空的函数隐藏在出队函数中,而此处的循环队列的销毁同顺序队列直接
delete。
1.3.4 链队列的结构及其操作函数:
- 先来看看链队列的结构定义:
- 要特别注意的一点是,链队列的队头指针和队尾指针是一个整体,
所以应当用一个结构体将他们包含起来。
- 要特别注意的一点是,链队列的队头指针和队尾指针是一个整体,
typedef int Elmenttype;
typedef Queue* PtrtoQueue;
typedef struct
{
Elmenttype data;
PtrtoQueue next;
}Queue;
typedef struct
{
PtrtoQueue Front;
PtrtoQueue Rear;
}LinkQueue;
- 链队列的初始化函数:
void CreatLinkQueue(LinkQueue& LQ)
{
LQ.Rear = LQ.Front = new Queue;
LQ.Front->next = NULL;
}
- 链队列的入队函数:
- 链队列不需要判断栈满的情况。
bool EnQueue(LinkQueue& LQ, Elmenttype X)
{
PtrtoQueue NewNode = new Queue;
NewNode->data = X;
NewNode->next = LQ.Rear->next;
LQ.Rear->next = NewNode;
LQ.Rear = NewNode;
}
- 链队列的判空的函数:
bool Empty(LinkQueue LQ)
{
if (LQ.Front == LQ.Rear)
{
return true;
}
return false;
}
- 链队列出队的函数:
bool DeQueue(LinkQueue& LQ, Elmenttype& X)
{
if (!Empty(LQ))
{
X = LQ.Front->next->data;
PtrtoQueue DelNode;
DelNode = LQ.Front->next;
LQ.Front->next = DelNode->next;
delete DelNode;
return true;
}
return false;
}
- 其实对链队列的操作本质上也是对单向链表的操作,只不过把重点集中在,尾插法和头删法上了而已。
1.3.5 队列的具体应用(有代码要求):
1.3.5.1那么不妨先思考一下,队列能做些什么呢?
- 一个比较重要且难的应用就是借用队列这个结构可以实现广度搜索,而广度搜索可以虽然搜索的效率低,但是能有找到最优解。
- 比如对二叉树结构的层序遍历,本质上也就是一种广度优先搜索,借用一个队列来存储树的每个结点,我们先让树的
根结点入队,然后当其出队后,让它的两个孩子入队,紧接着,又依次让它的两个孩子出队,每次一个孩子出队后,就让它的孩
子的孩子入队,依次往复,就能够实现一层一层地去遍历二叉树了。
- 比如对二叉树结构的层序遍历,本质上也就是一种广度优先搜索,借用一个队列来存储树的每个结点,我们先让树的
- 另外讲一个基础一点的应用吧,那就是处理实际问题中,需要对数据进行分队,然后再进行队与队之间操作的实例应用都可以
使用队列来实现。 - 对这个实际问题,我们其实首先就是对其进行男女的分队,这对应队列的操作就是,非空建队,也就是创建队列和入队的函数
的结合。再往后男女依次组成舞伴,其实就是出队的操作。所以这样看来的话,无非对队列应用的考虑要从两个角度出发:- 其一,就是数据要求满足先入先出特点的,我们使用队列。
- 其二,问题的实际应用的需求可以化为为 建队、入队和出队 三要素的逻辑过程的问题。
- 额外说一句,个人认为,其实数据结构就是多种具有某种特性的不同的逻辑结构,而去分析具体问题的编程,本质上也不过是
对具体问题进行逻辑抽象,把具体需求转化到对应数据结构的各种操作上,然后再去逐步考虑细节实现的方法,由主干到枝叶展
开,逐步完善而已。
1.3.5.2 部分相关代码:
- 舞伴问题的函数实现代码:
int QueueLen(SqQueue Q)//队列长度
{
int len = Q->rear - Q->front;
return len;
}
int EnQueue(SqQueue& Q, Person e)//加入队列
{
if (Q->rear == MAXQSIZE)
{
return ERROR;
}
Q->data[Q->rear++] = e;
}
int QueueEmpty(SqQueue& Q)//队列是否为空
{
if (Q->front == Q->rear)
{
return OK;
}
return ERROR;
}
int DeQueue(SqQueue& Q, Person& e)//出队列
{
if (QueueEmpty(Q))
{
return ERROR;
}
e = Q->data[Q->front++];
}
void DancePartner(Person dancer[], int num)//配对舞伴
{
Person man;
Person woman;
/*先分队*/
for (int i = 0; i < num; i++)
{
if (dancer[i].sex == 'F')
{
EnQueue(Fdancers, dancer[i]);
}
else
{
EnQueue(Mdancers, dancer[i]);
}
}
/*再出队配对*/
while (!QueueEmpty(Fdancers) && !QueueEmpty(Mdancers))
{
DeQueue(Fdancers,woman);
DeQueue(Mdancers, man);
cout << woman.name << " " << man.name << endl;
}
}
2.PTA实验作业(4分)
符号配对
银行业务队列简单模拟的代码
2.1 符号配对
2.1.1 解题思路及伪代码
解题思路:
- 首先要理清核心的思路,实现符号配对是运用栈来实现;
- 遍历输入数据时,遇到左符号就统一让它入栈;
- 而遇到右符号首先考虑栈是否为空:
- 如果栈为空,那就直接不匹配,直接输出缺少左符号;
- 如果栈不为空,那就判断当前的右符号是否与栈顶左符号匹配:
- 如果匹配,就让栈顶的元素出栈;
- 如果不匹配,就输出缺少右符号;
- 当遍历结束后,再次判断:
- 如果当下栈空;就代表所有的符号都配对,直接按全配对输出;
- 如果当下栈不空,就代表不配对,需要输出缺少右符号;
- 然后再去思考怎么解决该题的数据读入的问题,本次数据读入的结束点是按字面来看是一个’.‘后还有一个’endl’,
不过其实用一行一行读取的思想去看的话只需要读取到当当前读取的一行字符串是 “.” 时,表示结束就行。 - 再然后就是关于对"/" "/"这两个符号的处理,延续分别采用两个hash表来分别存储左右符号的思想,由于这两个
符号是由两个字符组成,所以就需要用string来存储,因此本次的hash表用string[]的形式来建表。 - 由于hash表是自己建的,所以得老老实实自己造Find函数。
伪代码如下:
//input
while(未到最后一行)
{
getline(单行str)
总str += 单行str;
}
//match
用string[]分别建好左右的符号表。
while(遍历总str中)
{
if(cur_sign为左符号) 执行push;
if (cur_sign为右符号)
{
if(stack不空)
{
if (左右符号匹配) 执行pop;
else 执行输出缺右符号
}
else 执行输出缺左符号
}
if(stack empty)-> all matched
else 执行输出缺右符号
}
//other function
遍历string[]找相同的string元素。
2.1.2 总结解题所用的知识点
- 一个没用成功的知识点:
getline(cin,string,end_char),getline函数可以设置一个char常量为输入的结束点。 - 使用了hash表的知识,用hash表来存储会用到的符号。
- 使用了STL库的string类。
- 学会了利用string类的特点对多行元素进行有指定结束标志的读取。
- 使用了STL库的stack类,学会使用pop、push、size等内联函数。
2.2 银行业务队列简单模拟
2.2.1 解题思路及伪代码
解题思路如下:
- 由于符合先入先出的数据特点,因此选择队列作为该题目的数据结构,
又由于本题不考虑复杂的出队和入队的问题,因此选择队列中的顺序队列。 - 首先要做的是根据已输入的数字情况的奇偶特性将输入数据分成两个队列。
- 然后再根据不同队列对应的不同窗口的业务处理特性进行不同的出队操作。
- 要另外注意输出格式。
伪代码如下:
输入顾客总数,
输入顾客编号组成的数组,
在输入数组数据的过程中,对编号进行判断
if(编号是奇数),向队列A执行入队操作。
if(编号是偶数),向队列B执行入队操作。
业务处理过程函数()。
以下是业务处理过程函数的伪代码,本质上是对队列执行出队操作
并按格式要求打印出出队的数据。
首先是对两个队列进行同时遍历
while(队A不空 && 队B不空)
{
先出队一次队A元素并打印(末尾有空格)
再次判断if(队A不空)
再出队一次队A元素并打印(末尾有空格)
再再次判断if(队A不空)
出队一次队B元素并打印(末尾有空格)
再再次判断if(队A为空 && 队列B仅剩一个元素)
出队一次队B元素并打印(末尾无空格)
}
//处理一个空一个不空的问题
while(A不为空)
{
若队列A仅剩一个元素时,出队一个队A元素并打印(末尾无空格)
若队列A不为空时,出队一个队A元素并打印(末尾有空格)
}
对队列B的处理同上。
2.2.2 总结解题所用的知识点
- 学会定义顺序队列并根据实际情况增加所需要的成员变量。
比如本题中需要增加计算成员个数的计数变量。 - 要根据实际情况写好对队列进行初始化的函数。该情况下,front代表的是队头元素的位置,
而rear则表示队尾元素的下一个位置。front和rear的起始位置都在0处。 - 要熟练掌握顺序队列的出队操作。
顺序队列的出队前要判断队列是否为空,空队列无法出队,空队列的判断条件是
当rear == front。出队的操作要求先保存出队元素再让front往前移动一个单位。
出队后要记得让计数变量减一。 - 要熟练掌握顺序队列的入队操作。
顺序队列的出队前要判断队列是否已满,满队列无法入队,满队列的判断条件是
当rear == maxsize。入队的操作要求先容纳入队元素再让rear往前移动一个单位。
入队后要记得让计数变量加一。 - 解决银行业务问题在本题中,本质上是处理两个队列的有格式要求的混合出队问题。
在代码框架上类似于合并两个有序数组的框架,不过内部的实际操作不同,此处以出队
操作为核心,同时这里还处理了在一层循环中对同一队列同时进行连续两次出队的操作,
该操作要求在第二次操作前判断该对象是否为空,避免数组越界引发程序崩溃。
3.阅读代码(0–1分)
3.1 题目及解题代码
class SortedStack {
public:
stack stk, help;
SortedStack() {
}
void push(int val) {
if (stk.empty()) stk.push(val);
else {
while (!stk.empty() && stk.top() < val) { //寻找储存栈中插入的位置(即,利用辅助栈help保存弹出元素
help.push(stk.top());
stk.pop();
}
stk.push(val); //找到合适位置后进行插入
while (!help.empty()) { //将之前弹出的元素重新导回储存栈
stk.push(help.top());
help.pop();
}
}
}
void pop() {
if (!stk.empty()) stk.pop();
}
int peek() {
return stk.empty() ? -1 : stk.top();
}
bool isEmpty() {
return stk.empty();
}
};
作者:wen-jian-69
链接:https://leetcode-cn.com/problems/sort-of-stacks-lcci/solution/cha-ru-pai-xu-si-xiang-by-wen-jian-69-4mxy/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3.2 该题的设计思路及伪代码
以下是原作者的设计思路
- 按照题目要求,就是要我们构造一个从栈底到栈顶的降序序列,因此可以参考插入排序,每次对元素val进行插入时先寻找其在有序序列的插入位置;
- 栈内寻找插入位置通过不断比较插入元素和栈顶元素的大小来实现;
- 若栈顶元素大于或等于插入元素,则可以直接入栈,若栈顶元素小于插入元素,则弹出栈顶,同时用辅助栈保存弹出的元素,
直到栈顶元素大于或等于插入元素,即可将val入栈,最后在将之前保存的弹出元素导回。
作者:wen-jian-69
链接:https://leetcode-cn.com/problems/sort-of-stacks-lcci/solution/cha-ru-pai-xu-si-xiang-by-wen-jian-69-4mxy/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
- 以下是我补充的伪代码:(尝试用英文来写)
insertOrder():
in every Push():
if (dataStack is empty) then push(val) into dataStack;
else
{
while(find the insert location)
{
if (val > topdata) then push(topdata) into helpStack and pop(it);
}
when we find the location by the above circulation
push(val) into dataStack;
and then push all data in helpStack into dataStack by another circulation.
}
* In the end,what need we do is to run this insertOrder function
each time we insert a new data. And we can get a descending order
stack from button to top.
* 由于只使用了一层循环以及只使用了一个辅助栈来解决问题,所以该问题的时间复杂度和空间复杂度都是线性阶O(n)。
3.3 分析该题目解题优势及难点。
- 这道题需要深刻理解栈结构先入后出的特性
- 这道题需要深刻理解插入排序集中于每一次插入先找位置后插入的要求。
- 简单来说这道题是栈结构与插入排序算法的结合应用。
- 难点在于想到用插入排序来解决只能使用另一个辅助栈来解决排序的限制,插入排序将排序的重点
微分到对每一个新元素查找插入位置的思维很妙。 - 单纯从代码来讲,这个代码依然使用到了三目运算符
exp1 ? exp2 : exp3说明这个运算符的使用很简洁,逻辑也很清晰,要学会使用。 - 单纯从代码来讲,本题的代码还有一个思想就是,对于需要在多个函数中使用的变量,比起在接口上频繁设置参数来不断传参,直接设置成全局变量则会方便很多!
4.通过Debug得到的一些感想。
- 对一道题目的分析,我们应该从主干开始,先把题目所要求实现的核心功能的思路先理清楚,
然后再逐步细化去详细探讨数据要如何输入,可能用到什么函数,以及某些特殊的细节点要怎
么特殊处理等等。 - 对题目进行分析的过程中,尤其是对分支情况进行分析的过程中,一定要格外慎重的注意,
分支的产生,必定包括了逻辑正面和逻辑反面,不能自以为是地只看到其中的一面就以为另
一面可以省略或者不考虑,有些不同分支的考虑,虽然逻辑结果相同,但是由于逻辑时序不同
所导向的结果也会有问题,所以请老老实实考虑每一个分支的正反两面!- 比如题目《符号配对》中的最后一个测试点,结果和栈不空的处理方式虽然一致,但是如果舍
弃了else分支,就不能让不配对的情况及时输出,在循环继续执行下去的过程中,无法避免来
自后面的元素对栈顶元素的影响,所以当最后循环结束时,难怕栈仍然不空,但是栈顶元素可
能已经不是当初判断不匹配时的那第一个不匹配的栈顶符号了。所以每个分支的逻辑出口都应该
慎重考虑,慎重处理!
- 比如题目《符号配对》中的最后一个测试点,结果和栈不空的处理方式虽然一致,但是如果舍