pythonsuper用法_python的super用法及含义
注释:以下都是在python2.7版本验证的
总括:1、python解决二义性问题,经历了深度优先算法、广度优先算法、拓扑排序算法,目前python的版本都是使用拓扑算法(C3)
2、严谨super(A,self).__init__()和A.__init__(self)这两种调用类方法的方法混用
3、A.__init__(self)是经典类的调用方法,使用深度优先算法,不论是否有类继承object;也就是新式类也可以使用这种调用方法
4、super(A,self).__init__()是新式类的调用方法,使用C3算,及拓扑算法;super也是一个类,不是一个方法,必须用到新式类上
5. super并不是一个函数,是一个类名,形如super(B, self)事实上调用了super类的初始化函数,产生了一个super对象;
6. super类的初始化函数并没有做什么特殊的操作,只是简单记录了类类型和具体实例;
7. super(B, self).func的调用并不是用于调用当前类的父类的func函数;使用C3算法,先搜索到func函数才是,父类的func函数不见得就一定先搜索到;super(self,C).func() #调用的并不是其父类C的func,而是C在MRO中的下一个类的func,不能再经典类中使用
8. Python的多继承类是通过mro的方式来保证各个父类的函数被逐一调用,而且保证每个父类函数只调用一次(如果每个类都使用super);
9. 混用super类和非绑定的函数是一个危险行为,这可能导致应该调用的父类函数没有调用或者一个父类函数被调用多次。
一、相关概念:
MRO:Method Resolution Order,即方法解析顺序,是python中用于处理二义性问题的算法
经典类: 反之,即不由任意内置类型派生出的类,则称之为“经典类”,mro使用“深度优先算法”
新式类:在Python 2及以前的版本中,由任意内置类型派生出的类(只要一个内置类型位于类树的某个位置),都属于“新式类”,都会获得所有“新式类”的特性;mro使用“拓扑算法,也成C3算法”;新式类,可以通过调用mro()函数和__mro__属性查看类的继承关系(方法:类名.mro(); 类名.__mro__)
python3.x: “新式类”和“经典类”的区分在Python 3之后就已经不存在,在Python 3.x之后的版本,因为所有的类都派生自内置类型object(即使没有显示的继承object类型),即所有的类都是“新式类”。
定义方式不同:
在Python 2.x 版本中,默认类都是旧式类,除非显式继承object。在Python 3.x 版本中,默认类就是新式类,无需显示继承object。
在Python 2.x 中,定义旧式类的方式:
class A: # A是旧式类,因为没有显示继承object
pass
class B(A): # B是旧式类,因为B的基类A是旧式类
pass
定义新式类的方式:
class A(object): # A是新式类,因为显式继承object
pass
class B(A): # B是新式类,因为B的基类A是新式类
pass
2. 保持class与type的统一
对新式类的实例执行a.__class__与type(a)的结果是一致的,对于旧式类来说就不一样了。
classA():pass
classB(object):passa=A()
b=B()printtype(a)print a.__class__
printtype(B)print B.__class__
printtype(b)print b.__class__输出:
__main__.A
[Finishedin 1.5s]
二、二义性:
python支持多继承,多继承的语言往往会遇到以下两类二义性的问题:
有两个基类A和B,A和B都定义了方法f(),C继承A和B,那么调用C的f()方法时会出现不确定。
有一个基类A,定义了方法f(),B类和C类继承了A类(的f()方法),D类继承了B和C类,那么出现一个问题,D不知道应该继承B的f()方法还是C的f()方法。
python中通过C3算法很好的避免了以上两类二义性的情况。
深度优先算法(DFS,Depth-First-Search)
把根节点压入栈中。
每次从栈中弹出一个元素,搜索所有在它下一级的元素,把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。
找到所要找的元素时结束程序。
如果遍历整个树还没有找到,结束程序。
广度优先算法(BFS,Breadth-First-Search)
把根节点放到队列的末尾。
每次从队列的头部取出一个元素,查看这个元素所有的下一级元素,把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。
找到所要找的元素时结束程序。
如果遍历整个树还没有找到,结束程序。
拓扑排序:
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑排序(TopologicalOrder)的序列,简称拓扑序列。
拓扑排序的实现步骤:
循环执行以下两步,直到不存在入度为0的顶点为止
选择一个入度为0的顶点并输出之;
从网中删除此顶点及所有出边。
python中调用父类方法的两种方式:
classA(object):def __init__(self):
self.name= "A: name"
print "A:__init__"
deffun(self):print "A:fun"
classB(A):def __init__(self):print "B:__init__"A.__init__(self) #使用类名直接调用
super(B, self).__init__() #使用super关键字调用
deffun(self):print "B:fun"A.fun(self)
super(B, self).fun()print self.name
对于单继承来说,上面这两种方式并无本质上的区别,但是当出现多继承的时候,super得到的基类就不一定是我们“认为”的基类了,我们看下面这个例子:
classA(object):def __init__(self):print "enter A"
print "leave A"
classB(object):def __init__(self):print "enter B"
print "leave B"
classC(A):def __init__(self):print "enter C"super(C, self).__init__()print "leave C"
classD(A):def __init__(self):print "enter D"super(D, self).__init__()print "leave D"
classE(B, C):def __init__(self):print "enter E"B.__init__(self)
C.__init__(self)print "leave E"
classF(E, D):def __init__(self):print "enter F"E.__init__(self)
D.__init__(self)print "leave F"f= F()
输出结果:
enter F
enter E
enter B
leave B
enter C
enter D
enter A
leave A
leave D
leave C
leave E
enter D
enter A
leave A
leave D
leave F
类的继承关系如下所示:
object
| \
| A
| / |
B C D
\ / |
E |
\ |
F
我们的本意是希望调用构造函数的时候,对于基类的构造方法也进行调用,但是实际结果发现,A和D的构造函数被调用了2次,而且奇怪的是,当调用super(C, self).__init__()的时候,竟然进入D的构造函数,这也是为什么D的构造函数被调用了两次(一次是F调用的,一次是C调用的)!从继承关系上看,C的基类应该是A才对。这就要引出下面要解释的,python中的C3方法。不过针对上面这个例子,修改的思路很简单,要么全部使用类名来调用基类方法,要么全部使用super()来调用,不要混用!
三、C3算法的演变历史:
经典类(python 2.2之前):
在python 2.2之前,python中使用经典类(classicclass),经典类是一种没有继承的类,所有类型都是type类型,如果经典类作为父类,子类调用父类构造函数会报错。当时用作MRO的算法是DFS(深度优先),下面的例子是当时使用DFS算法的示例(向右是基类方向):
正常的继承方式:
A->B->D
A->C->E
DFS的遍历顺序为:A->B->D->C->E
这种情况下,不会产生问题。
菱形的继承方式
A->B->D
A->C->D
DFS的遍历顺序为:A->B->D->C
对于这种情况,如果公共父类D中也定义了f(),C中重写了方法f(),那么C中的f()方法永远也访问不到,因为按照遍历的顺序始终先发现D中的f()方法,导致子类无法重写基类方法。
新式类(python2.2):
在python2.2开始,为了使类的内置类型更加统一,引入了新式类(new-style class),新式类每个类都继承自一个基类,默认继承自object,子类可以调用基类的构造函数。由于所有类都有一个公共的祖先类object,所以新式类不能使用DFS作为MRO。在当时有两种MRO并存:
如果是经典类,MRO使用DFS
如果是新式类,MRO使用BFS
针对新式类的BFS示例如下(向右是基类方向):
正常继承方式:
A->B->D
A->C->E
BFS的遍历顺序为:A->B->C->D->E
D是B的唯一基类,但是遍历时却先遍历节点C,这种情况下应该先从唯一基类进行查找,这个原则称为单调性。
菱形的继承方式
A->B->D
A->C->D
BFS的遍历顺序为:A->B->C->D
BFS解决了前面提到的子类无法重写基类方法的问题。
经典类和新式类并存(python2.3-python2.7),C3算法产生:
由于DFS和BFS针对经典类和新式类都有缺陷,从python2.3开始,引入了C3算法。针对前面两个例子,C3算法的遍历顺序如下:
正常继承方式:
A->B->D
A->C->E
C3的遍历顺序为:A->B->D->C->E
菱形的继承方式
A->B->D
A->C->D
C3的遍历顺序为:A->B->C->D
看起来是DFS和BFS的综合,但是并非如此,下面的例子说明了C3算法的具体实现:
从前面拓扑排序的定义可知,将有向无环图进行拓扑排序后,按照得到的拓扑序列遍历即可满足单调性,原因是由根到叶即是子类到基类的方向,当基类的入度为0是,它就是子类的唯一基类,此时会优先遍历此基类,符合单调性。而子类无法重写方法的问题也可以得到解决,因为当多个子类继承自同一个基类时,该基类的入度不会先于子类减为0,所以可以保证优先遍历入度减为0的子类。
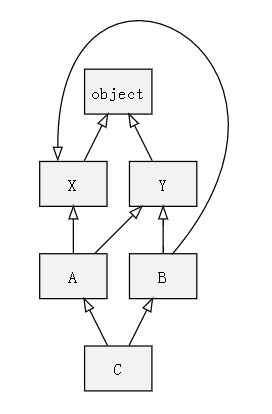
结合下面这张图的例子来说明C3算法的执行步骤(图中箭头由子类指向父类):
首先找入度为0的点,只有A,把A取出,把A相关的边去掉,再找下一个入度为0的点,B和C满足条件,从左侧开始取,取出B,这时顺序是AB,然后去掉B相关的边,这时候入度为0的点有E和C,依然取左边的E,这时候顺序为ABE,接着去掉E相关的边,这时只有一个点入度为0,那就是C,取C,顺序为ABEC。去掉C的边得到两个入度为0的点D和F,取出D,顺序为ABECD,然后去掉D相关的边,那么下一个入度为0的就是F,然后是object。所以最后的排序就为ABECDFobject。
了解了C3算法,我们前面那个混用的例子中调用super(C,self).__init__()会去调用D构造函数的原因也就显而易见了。
在python中提供了__mro__内置属性来查看类的MRO,例如:
classD(object):pass
classE(object):pass
classF(object):pass
classC(D, F):pass
classB(E, D):pass
classA(B, C):pass
print A.__mro__
print A.mro()
#输出:(, , , , , , )
再举一个例子:
classA(object):def __init__(self):print "A"
classB(object):def __init__(self):print "B"
classC(object):def __init__(self):print "C"
classD(A,B,C):def __init__(self):
super(D,self).__init__()
super(A,self).__init__()
super(B,self).__init__()
super(C,self).__init__()
X= D()
print D.mro()
# D-->A-->B-->C-->object D的直接父类是A,A的直接父类是B,。。。。
输出是:
A
B
C
[, , , , ]
[Finished in 1.2s]
会发现:
super(D,self).__init__()
执行的是A.__init__()
super(A,self).__init__()
执行的是B.__init__()
super(B,self).__init__()
执行的是C.__init__()
super(C,self).__init__()
执行的是Object.__init__()
这是因为mro(D)为:[ D, A, B, C, Object]
mro的C3算法,参考这篇文章:https://www.cnblogs.com/whatisfantasy/p/6046991.html
我们把类 C 的线性化(MRO)记为 L[C] = [C1, C2,…,CN]。其中 C1 称为 L[C] 的头,其余元素 [C2,…,CN] 称为尾。如果一个类 C 继承自基类 B1、B2、……、BN,那么我们可以根据以下两步计算出 L[C]:
L[object] = [object]
L[C(B1…BN)] = [C] + merge(L[B1]…L[BN], [B1]…[BN])
这里的关键在于 merge,其输入是一组列表,按照如下方式输出一个列表:
检查第一个列表的头元素(如 L[B1] 的头),记作 H。
若 H 未出现在其它列表的尾部(又是头又是尾的除外),则将其输出,并将其从所有列表中删除,然后回到步骤1;否则,取出下一个列表的头部记作 H,继续该步骤。
重复上述步骤,直至列表为空或者不能再找出可以输出的元素。如果是前一种情况,则算法结束;如果是后一种情况,说明无法构建继承关系,Python 会抛出异常。
根据图示,查看各个类的线性化结果
L[object] = [object]
L[X] = L[X(object)] = [X]+merge(L[object]+[object]) = [X] + merge([object] + [object]) = [X] + [object] = [X, object]
L[Y] = [Y, object]
L[A] = L[A(X,Y)] = [A] + merge(L[X], L[Y], [X], [Y]) = [A] + merge([X, object], [Y, object], [X], [Y]) = [A, X] + merge([object], [Y, object], [Y]) = [A, X, Y] + merge([object], [object]) = [A, X, Y, object]
转载:
1、http://blog.csdn.net/qwertyupoiuytr/article/details/56439134
2、https://www.cnblogs.com/blackmatrix/p/5630515.html