【算法专题】二分查找
二分查找
- 二分查找
-
- 1. 二分查找
- 2. 在排序数组中查找元素的第一和最后一个位置
- 3. 搜索插入位置
- 4. x 的平方根
- 5. 山脉数组的峰顶索引
- 6. 寻找峰值
- 7. 寻找旋转排序数组中的最小值
- 8. 点名
二分查找
1. 二分查找
题目链接 -> Leetcode -704.二分查找
Leetcode -704.二分查找
题目:给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 - 1。
示例 1:
输入: nums = [-1, 0, 3, 5, 9, 12], target = 9
输出 : 4
解释 : 9 出现在 nums 中并且下标为 4
示例 2 :
输入 : nums = [-1, 0, 3, 5, 9, 12], target = 2
输出 : -1
解释 : 2 不存在 nums 中因此返回 - 1
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在[1, 10000]之间。
nums 的每个元素都将在[-9999, 9999]之间。
思路:
-
定义 left , right 指针,分别指向数组的左右区间。
-
找到待查找区间的中间点 mid ,找到之后分三种情况讨论:
- arr[mid] == target 说明正好找到,返回 mid 的值;
- arr[mid] > target 说明 [mid, right] 这段区间都是大于 target 的,因此舍去右边区间,在左边 [left, mid -1] 的区间继续查找,即让 right = mid - 1 ,然后重复 2 过程;
- arr[mid] < target 说明 [left, mid] 这段区间的值都是小于 target 的,因此舍去左边区间,在右边 [mid + 1, right] 区间继续查找,即让 left = mid + 1 ,然后重复 2 过程;
- 当 left 与 right 错开时,说明整个区间都没有这个数,返回 -1 。
代码如下:
class Solution {
public:
int search(vector& nums, int target)
{
int left = 0, right = nums.size() - 1;
while (left <= right)
{
int mid = left + (right - left) / 2; // 防止溢出
if (nums[mid] > target) right = mid - 1; // 中间数比 target 大,改变右指针
else if (nums[mid] < target) left = mid + 1; // 中间数比 target 小,改变左指针
else return mid; // 找到返回下标
}
return -1;
}
};
2. 在排序数组中查找元素的第一和最后一个位置
题目链接 -> Leetcode -34.在排序数组中查找元素的第一和最后一个位置
Leetcode -34.在排序数组中查找元素的第一和最后一个位置
题目:给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回[-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5, 7, 7, 8, 8, 10], target = 8
输出:[3, 4]
示例 2:
输入:nums = [5, 7, 7, 8, 8, 10], target = 6
输出:[-1, -1]
示例 3:
输入:nums = [], target = 0
输出:[-1, -1]
提示:
- 0 <= nums.length <= 10^5
- 10^9 <= nums[i] <= 10^9
nums 是一个非递减数组 - 10^9 <= target <= 10^9
思路:二分思想,就是根据数据的性质,在某种判断条件下将区间一分为二,然后舍去其中一个区间,然后再另一个区间内查找;为了方便叙述,用 x 表示该元素, resLeft 表示左边界, resRight 表示右边界;
寻找左边界思路:
我们注意到以左边界划分的两个区间的特点:
- 左边区间 [left, resLeft - 1] 都是小于 x 的;
- 右边区间(包括左边界) [resLeft, right] 都是大于等于 x 的;
因此,关于 mid 的落点,我们可以分为下面两种情况:
- 当我们的 mid 落在 [left, resLeft - 1] 区间的时候,也就是 arr[mid] < target 。说明 [left, mid] 都是可以舍去的,此时更新 left 到 mid + 1 的位置,继续在 [mid + 1, right] 上寻找左边界;
- 当 mid 落在 [resLeft, right] 的区间的时候,也就是 arr[mid] >= target 。说明 [mid + 1, right] (因为 mid 可能是最终结果,不能舍去)是可以舍去的,此时更新 right 到 mid 的位置,继续在 [left, mid] 上寻找左边界;
注意:这里找中间元素需要向下取整。因为后续移动左右指针的时候:
- 左指针: left = mid + 1 ,是会向后移动的,因此区间是会缩小的;
- 右指针: right = mid ,可能会原地踏步(比如:如果向上取整的话,如果剩下 1,2 两个元素, left == 1 , right == 2 , mid == 2 。更新区间之后, left,right,mid 的值没有改变,就会陷入死循环)。因此一定要注意,当 right = mid 的时候,要向下取整。
同理大家可以尝试分析寻找右边界的思路。
代码如下:
class Solution {
public:
vector searchRange(vector& nums, int target)
{
if (nums.size() == 0) return { -1, -1 };
int left = 0, right = nums.size() - 1;
int begin = -1;
// 寻找左端点
while (left < right)
{
// 当元素个数为偶数个时,取左边的为中间元素,因为要找的是左边界
int mid = left + (right - left) / 2;
if (nums[mid] < target) left = mid + 1;
else right = mid;
}
if (target == nums[left]) begin = left;
else return { -1, -1 };
left = 0, right = nums.size() - 1;
// 寻找右端点
while (left < right)
{
// 当元素个数为偶数个时,取右边的为中间元素,因为要找的是右边界
// 或者当更新 right / left 时出现 -1 取mid的时候就要+1
int mid = left + (right - left + 1) / 2;
if (nums[mid] > target) right = mid - 1;
else left = mid;
}
return { begin, right };
}
};
3. 搜索插入位置
题目链接 -> Leetcode -35.搜索插入位置
Leetcode -35.搜索插入位置
题目:给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1, 3, 5, 6], target = 5
输出 : 2
示例 2 :
输入 : nums = [1, 3, 5, 6], target = 2
输出 : 1
示例 3 :
输入 : nums = [1, 3, 5, 6], target = 7
输出 : 4
提示 :
- 1 <= nums.length <= 10^4
- 10^4 <= nums[i] <= 10^4
nums 为 无重复元素 的 升序 排列数组 - 10^4 <= target <= 10^4
思路与上题思路类似,寻找目标值的左边界即可。
代码如下:
class Solution {
public:
int searchInsert(vector& nums, int target)
{
// 如果插入的位置在最后
if (nums[nums.size() - 1] < target) return nums.size();
int left = 0, right = nums.size() - 1;
// 二分查找找左边界
while (left < right)
{
int mid = left + (right - left) / 2;
if (nums[mid] < target) left = mid + 1;
else right = mid;
}
return left;
}
};
4. x 的平方根
题目链接 -> Leetcode -69.x 的平方根
Leetcode -69.x 的平方根
题目:给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 2^31 - 1
思路也和上题类似,寻找右边界即可;
代码如下:
class Solution {
public:
int mySqrt(int x)
{
// long long 防止溢出
long long left = 0, right = x;
// 二分查找寻找右边界
while (left < right)
{
long long mid = left + (right - left + 1) / 2;
if (mid * mid > x) right = mid - 1;
else left = mid;
}
return left;
}
};
5. 山脉数组的峰顶索引
题目链接 -> Leetcode -825.山脉数组的峰顶索引
Leetcode -825.山脉数组的峰顶索引
题目:符合下列属性的数组 arr 称为 山脉数组 :
arr.length >= 3
存在 i(0 < i < arr.length - 1)使得:
arr[0] < arr[1] < … arr[i - 1] < arr[i]
arr[i] > arr[i + 1] > … > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ,返回满足 arr[0] < arr[1] < … arr[i - 1] < arr[i] > arr[i + 1] > … > arr[arr.length - 1] 的下标 i 。
你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。
示例 1:
输入:arr = [0, 1, 0]
输出:1
示例 2:
输入:arr = [0, 2, 1, 0]
输出:1
示例 3:
输入:arr = [0, 10, 5, 2]
输出:1
提示:
3 <= arr.length <= 10^5
0 <= arr[i] <= 10^6
题目数据保证 arr 是一个山脉数组
思路:
- 分析峰顶位置的数据特点,以及山峰两旁的数据的特点:
- 峰顶数据特点: arr[i] > arr[i - 1] && arr[i] > arr[i + 1] ;
- 峰顶左边的数据特点: arr[i] > arr[i - 1] && arr[i] < arr[i + 1] ,也就是呈现上升趋势;
- 峰顶右边数据的特点: arr[i] < arr[i - 1] && arr[i] > arr[i + 1] ,也就是呈现下降趋势。
- 因此,根据 mid 位置的信息,我们可以分为下面三种情况:
- 如果 mid 位置呈现上升趋势,说明我们接下来要在 [mid + 1, right] 区间继续搜索;
- 如果 mid 位置呈现下降趋势,说明我们接下来要在 [left, mid - 1] 区间搜索;
- 如果 mid 位置就是山峰,直接返回结果。
代码如下:
class Solution {
public:
int peakIndexInMountainArray(vector& arr)
{
int left = 0,right = arr.size() - 1;
// 符合二段性,就可以用二分查找
while(left < right)
{
int mid = left + (right - left + 1)/2;
if(arr[mid] > arr[mid - 1]) left = mid;
else right = mid - 1;
}
return left;
}
};
6. 寻找峰值
题目链接 -> Leetcode -162.寻找峰值
Leetcode -162.寻找峰值
题目:峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1, 2, 3, 1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1, 2, 1, 3, 5, 6, 4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
提示:
- 1 <= nums.length <= 1000
- 2^31 <= nums[i] <= 2^31 - 1
- 对于所有有效的 i 都有 nums[i] != nums[i + 1]
思路:寻找二段性:
任取⼀个点 i ,与下一个点 i + 1 ,会有如下两种情况:
- arr[i] > arr[i + 1] :此时「左侧区域」一定会存在山峰(因为最左侧是负无穷,但此时还没有下降趋势),那么我们可以去左侧去寻找结果;
- arr[i] < arr[i + 1] :此时「右侧区域」一定会存在山峰(因为最右侧是负无穷,但此时还没有下降趋势),那么我们可以去右侧去寻找结果。
当我们找到「二段性」的时候,就可以尝试用「二分查找」算法来解决问题。
代码如下:
class Solution {
public:
int findPeakElement(vector& nums)
{
int left = 0, right = nums.size() - 1;
// 符合二段性,可以用二分查找
while(left < right)
{
int mid = left + (right - left)/2;
if(nums[mid] > nums[mid + 1]) right = mid;
else left = mid + 1;
}
return left;
}
};
7. 寻找旋转排序数组中的最小值
题目链接 -> Leetcode -153.寻找旋转排序数组中的最小值
Leetcode -153.寻找旋转排序数组中的最小值
题目:已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0, 1, 2, 4, 5, 6, 7] 在变化后可能得到:
若旋转 4 次,则可以得到[4, 5, 6, 7, 0, 1, 2]
若旋转 7 次,则可以得到[0, 1, 2, 4, 5, 6, 7]
注意,数组[a[0], a[1], a[2], …, a[n - 1]] 旋转一次 的结果为数组[a[n - 1], a[0], a[1], a[2], …, a[n - 2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3, 4, 5, 1, 2]
输出:1
解释:原数组为[1, 2, 3, 4, 5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4, 5, 6, 7, 0, 1, 2]
输出:0
解释:原数组为[0, 1, 2, 4, 5, 6, 7] ,旋转 4 次得到输入数组。
示例 3:
输入:nums = [11, 13, 15, 17]
输出:11
解释:原数组为[11, 13, 15, 17] ,旋转 4 次得到输入数组。
提示:
- n == nums.length
- 1 <= n <= 5000
- 5000 <= nums[i] <= 5000
nums 中的所有整数 互不相同
nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
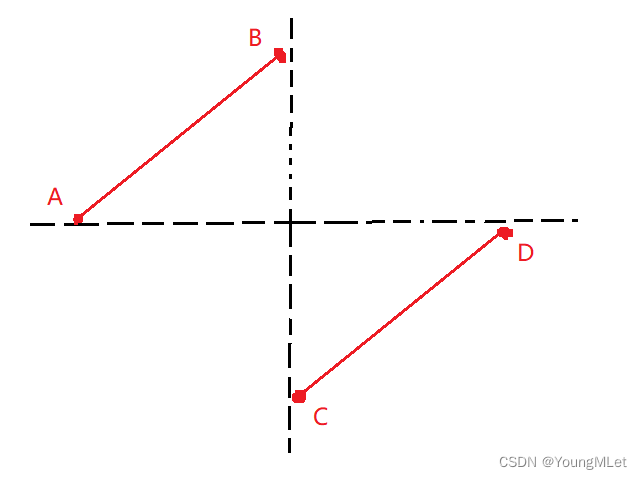
思路:题目中的数组规则如下图所示:
其中 C 点就是我们要求的点。
二分的本质:找到一个判断标准,使得查找区间能够一分为二。
通过图像我们可以发现, [A,B] 区间内的点都是严格大于 D 点的值的, C 点的值是严格小于 D 点的值的。但是当 [C,D] 区间只有一个元素的时候, C 点的值是可能等于 D 点的值的。
因此,初始化左右两个指针 left , right :
然后根据 mid 的落点,我们可以这样划分下一次查询的区间:
- 当 mid 在 [A,B] 区间的时候,也就是 mid 位置的值严格大于 D 点的值,下一次查询区间在 [mid + 1,right] 上;
- 当 mid 在 [C,D] 区间的时候,也就是 mid 位置的值严格小于等于 D 点的值,下次查询区间在 [left,mid] 上。
当区间长度变成 1 的时候,就是我们要找的结果。
代码如下:
class Solution {
public:
int findMin(vector& nums)
{
int left = 0, right = nums.size() - 1;
while(left < right)
{
// 以最右边的元素为目标进行比较
int mid = left + (right - left )/2;
if(nums[mid] > nums[nums.size() - 1]) left = mid + 1;
else right = mid;
}
return nums[left];
}
};
8. 点名
题目链接 -> Leetcode -LCR 173.点名
Leetcode -LCR 173.点名
题目:某班级 n 位同学的学号为 0 ~n - 1。点名结果记录于升序数组 records。假定仅有一位同学缺席,请返回他的学号。
示例 1:
输入: records = [0, 1, 2, 3, 5]
输出 : 4
示例 2 :
输入 : records = [0, 1, 2, 3, 4, 5, 6, 8]
输出 : 7
提示:
1 <= records.length <= 10000
思路是以数组下标为目标对象进行比较,寻找左边界即可;
代码如下:
class Solution {
public:
int missingNumber(vector& nums)
{
int left = 0, right = nums.size() - 1;
while(left < right)
{
// 以数组下标为目标对象进行比较
int mid = left + (right - left)/2;
if(nums[mid] > mid) right = mid;
else left = mid + 1;
}
return left == nums[left]? left + 1 : left;
}
};