分油问题C++求解

原题

3个油桶，容量分别为（大桶）20，（中桶）9，（小桶）7，初始时大桶满油，如何操作可以分出17的油？

代码

#include
#include
#include
#include
using namespace std;

class R {
	public:
		int l,v;
};

class T {
	public:
		R a,b,c;
		int last;
		string xw;
		T(R a,R b,R c):a(a),b(b),c(c) {
		}
		T(R a,R b,R c,int last,string xw):a(a),b(b),c(c),last(last),xw(xw) {
		}
		int id() {
			return a.v*100+b.v*10+c.v;
		}
};

void go(R *r1,R *r2) {
	int v=r2->v+r1->v;
	v=min(v,r2->l);
	int cha=v-r2->v;
	r2->v=v;
	r1->v-=cha;
}

void dfs(vector vt,T t) {
	if(t.last==-1){
		cout<> "<> "< s;
	queue q;
	q.push(t);
	s.insert(t.id());
	vector vt;

	while(!q.empty()) {
		t=q.front();
		q.pop();
		if(t.a.v==targetV || t.b.v==targetV || t.c.v==targetV) {
			cout<<"Success"<0) {
			if(b.vb");
				go(&(temp.a),&(temp.b));
				int id=temp.id();
				if(s.find(id)==s.end()) {
					q.push(temp);
					s.insert(id);
				}
			}
			if(c.vc");
				go(&(temp.a),&(temp.c));
				int id=temp.id();
				if(s.find(id)==s.end()) {
					q.push(temp);
					s.insert(id);
				}
			}
		}

		if(b.v>0) {
			if(a.va");
				go(&(temp.b),&(temp.a));
				int id=temp.id();
				if(s.find(id)==s.end()) {
					q.push(temp);
					s.insert(id);
				}
			}
			if(c.vc");
				go(&(temp.b),&(temp.c));
				int id=temp.id();
				if(s.find(id)==s.end()) {
					q.push(temp);
					s.insert(id);
				}
			}
		}

		if(c.v>0) {
			if(a.va");
				go(&(temp.c),&(temp.a));
				int id=temp.id();
				if(s.find(id)==s.end()) {
					q.push(temp);
					s.insert(id);
				}
			}
			if(b.vb");
				go(&(temp.c),&(temp.b));
				int id=temp.id();
				if(s.find(id)==s.end()) {
					q.push(temp);
					s.insert(id);
				}
			}
		}
	}

	return 0;
}

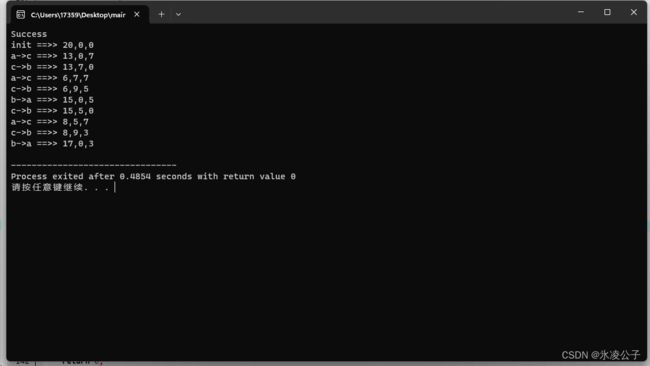
运行

解析

1.每个桶有它的容量以及目前油量，数据结构定义为

class R {
	public:
		int l,v;
};

 表示容量和油量

2.每次操作可以从一个非空桶尽可能倒油到另一个非满桶【因为倒到满桶没有意义】，这个一定要理解，倒油实现函数为

void go(R *r1,R *r2) {
	int v=r2->v+r1->v;
	v=min(v,r2->l);
	int cha=v-r2->v;
	r2->v=v;
	r1->v-=cha;
}

因为被倒入的桶容量有限，所以要做个较小值判断

3.每完成一次倒油操作，做一次记录，记录下当前3个油桶的油量，以及这个操作【从哪个桶倒入另一个桶的】，数据结构定义为

class T {
	public:
		R a,b,c;
		int last;
		string xw;
		T(R a,R b,R c):a(a),b(b),c(c) {
		}
		T(R a,R b,R c,int last,string xw):a(a),b(b),c(c),last(last),xw(xw) {
		}
		int id() {
			return a.v*100+b.v*10+c.v;
		}
};

其中我们求解出结果之后需要将这些操作都打印出来，所以需要一个列表来存储我们的步骤

vector vt;

那么T.last这个属性就是上一步操作在列表中的下标，方便查找

T.xw表示上一步操作的行为，若T.xw=="a->b"，则表示油从a桶倒入b桶。

4.开一个队列来模拟倒油过程，直到有一个操作满足我们的需求，打印倒油过程并退出。

5.有可能没有方案做得到，所以我们需要对每次的方案做标识，避免重复的局面入队，比如：我刚将大桶的油倒入小桶，此时从[20,0,0]=>[13,0,7]，紧接着又把油从小桶倒回大桶，这种情况我们需要排除掉，其中T.id这个函数就是表示状态的标识，只要三个桶的油量出现过这种状况，就表示已经做过类似的操作了，此时这个操作就不要入队了。