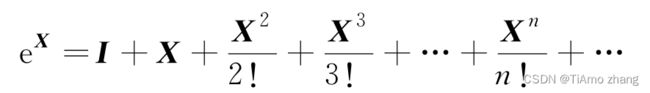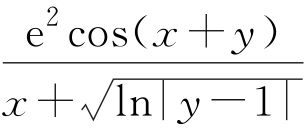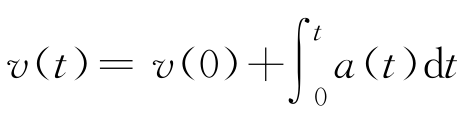MATLAB实战 | 求矩阵指数、预定义变量i和j的含义以及梯形积分法

 

01、求矩阵指数应用实战

【例1】根据矩阵指数的幂级数展开式求矩阵指数。

 设X是给定的矩阵，E是矩阵指数函数值，F是展开式的项，n是项数，循环一直进行到F很小，以至于F值加在E上对E的值影响不大时为止。为了判断F是否很小，可利用矩阵范数的概念。矩阵A的范数的一种定义是

。在MATLAB中用norm(A,1)函数来计算。所以当norm(F,1)=0时，认为F很小，应退出循环的执行。程序如下：

X = input('Enter X:')
E= zeros(size(X));
E = eye( size(X));
n=1;
while norm(E,1)> 0
E=E+F;
end
E
E=E*X/n;
n=n+1;
expm(X)  //调用 MATLAB 矩阵指数函数求矩阵指数

程序运行结果如下：

 

 运行结果表明，程序运行结果与MATLAB矩阵指数函数expm(X)的结果一致。本程序涉及矩阵运算，初学者可能不太习惯。如果能分析一下程序的执行过程，对领会编程思想是有益的。另外，我们知道矩阵乘法的交换律不成立，但这里要请大家分析一下程序中的语句F=F*X/n可否写成F= X * F /n，为什么？

02、预定义变量i和j的含义---变量与赋值

1. 变量命名

在MATLAB中，变量名是以字母开头，后跟字母、数字或下画线的字符序列，最多63个字符。例如，x、x_1、x2均为合法的变量名。在MATLAB中，变量名区分字母的大小写，这样，score、Score和SCORE表示3个不同的变量。另外，不能使用MATLAB的关键字作为变量名，例如if、end、for。

注意/

定义变量时应避免创建与预定义变量、函数同名的变量，例如i、j、power、int16、format、path等。一般情况下，变量名称优先于函数名称。如果创建的变量使用了某个函数的名称，可能导致计算过程、计算结果出现意外情况。可以使用exist或which函数检查拟用名称是否已被使用。如果不存在与拟用名称同名的变量、函数或M文件，exist函数将返回0，否则返回一个非零值。例如：

>> exist power
ans =
5
>> exist Power
ans =
0

which函数用来定位函数和文件，如果函数或文件存在，则显示其完整的路径。例如：

>> which power
built-in (C:Program Files MATLAB\R2022a toolbox matlab ops) //char power
> which powerl

未找到power1'

 

2. 赋值语句

MATLAB赋值语句有两种格式：

变量=表达式

表达式

其中，表达式是用运算符将有关运算量连接起来的式子。执行第一种语句，MATLAB将右边表达式的值赋给左边的变量; 执行第二种语句，将表达式的值赋给MATLAB的预定义变量ans。看下列命令的执行结果。

 一般情况下，运算结果在命令行窗口中显示出来。如果在命令的最后加分号，那么，MATLAB仅仅执行赋值操作，不显示运算的结果。如果运算的结果是一个很大的矩阵或不需要运算结果，则可以在命令的最后加上分号。

【例2】 当x=π/2，y=1+3i时，求表达式

的值。

在MATLAB命令行窗口分别输入命令：

>> x= pi/2;
>> y=1+3i;
>> z= exp(2) * cos(x+ y)/(x+ sqrt(log(abs(y-1)))) //计算表达式的值
z = 
-23.9018 -15.2713i

3. 预定义变量

在MATLAB中，提供了一些系统定义的特殊变量，这些变量称为预定义变量。表1列出了一些常用的预定义变量。预定义变量有特定的含义，在使用时一般尽量避免对这些变量重新赋值，但对它们赋值也不会出错，只是会覆盖原来的值，用clear命令清除后即可恢复原来的值。

■ 表1 常用的预定义变量

 MATLAB提供了isfinite函数用于判定数据对象是否为有限值，isinf函数用于判定数据对象是否为无限值，isnan函数用于确定数据对象中是否含有NaN值。

注意/

MATLAB预定义变量有特定的含义，在使用时应尽量避免对这些变量重新赋值。以i或j为例，在MATLAB中，i和j代表虚数单位，如果给i或j重新赋值，就会覆盖掉原来虚数单位的定义，这时可能会导致一些很隐蔽的错误。例如，由于习惯的原因，程序中通常使用i或j作为循环变量，这时如果有复数运算就会导致错误，因此，不要用i或j作为循环变量名，除非确认在程序运行期间不会和复数打交道，或者使用像7+5i这样的复数记法，而不用7+5*i，前者是一个复数常量，后者是一个表达式，即将i看成一个运算量，参与表达式的运算。也可以在使用i作为循环变量时，换用j表示复数。

03、 梯形积分法

在MATLAB中，提供了函数trapz对由表格形式定义的离散数据用梯形法求定积分，函数调用格式如下:

(1) T=trapz(Y)。这种格式用于求均匀间距的积分。通常，输入参数Y是向量，采用单位间距(即间距为1)，计算Y的近似积分。若Y是矩阵，则输出参数T是一个行向量，T的每个元素分别存储Y的每一列的积分结果。例如：

若间距不为1，例如求

，则可以采用以下命令：

 

(2) T=trapz(X,Y)。这种格式用于求非均匀间距的积分。通常，输入参数X、Y是两个等长的向量，X、Y满足函数关系Y = f(X)， 按X指定的数据点间距，对Y求积分。若X是有m个元素的向量，Y是m×n矩阵，则输出参数T是一个有n个元素的向量，T的每个元素分别存储Y的每一列的积分结果。

【例3】从地面发射一枚火箭，表2记录了在0~80s火箭的加速度。试求火箭在第80s时的速度。

■ 表2 火箭发射加速度

 

设速度为v(t)，则

，这样就把问题转化为求积分的问题。命令如下：