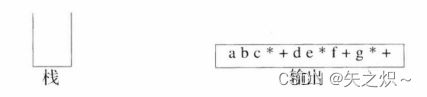第3章 表、栈和队列

3.3 栈ADT

3.3.1 栈模型

        栈是限制插入和删除只能在一个位置上进行的表，该位置是表的末端，叫作栈的顶(top)。对栈的基本操作有Push(进栈)和Pop(出栈)，前者相当于插入，后者则是删除最后插入的元素。最后插入的元素可以通过使用Top例程在执行Pop之前进行检查。对空栈进行的Pop或Top一般被认为是栈ADT的错误。另一方面，当运行Push时空间用尽是一个实现错误，但不是ADT错误。

        栈有时又叫作LIFO(后进先出)表。在图3-37 中描述的模型只象征着Push 是输入操作而 Pop 和 Top是输出操作。普通的清空栈的操作和判断是否空栈的测试都是栈的操作指令系统的一部分，但是，对栈所能够做的基本上也就是Push和Pop操作。

        图3-38表示在进行若干操作后的一个抽象的栈。一般的模型是，存在某个元素位于栈顶，而该元素是唯一的可见元素。

3.3.2 栈的实现

        由于栈是一个表，因此任何实现表的方法都能实现栈。我们将给出两种流行的实现方法，一种方法使用指针，而另一种方法则使用数组。但是，正如我们在前一节看到的，如果使用好的编程原则，那么调用例程不必知道使用的是哪种方法。

1.栈的链表实现

        栈的第一种实现方法是使用单链表。我们通过在表前端插入来实现Push，通过删除表前端元素实现Pop。Top操作只是检查表前端元素并返回它的值。有时Pop操作和Top操作合二为一。我们本可以使用前一节的链表例程，但为了清楚起见我们还是从头开始重写栈的例程。

        首先，我们在图3-39中给出一些定义。实现栈要用到一个表头。图3-40表明测试空栈与测试空表的方式相同。

#ifndef _Stack_h

struct Node;
typedef struct Node *PtrToNode;
typedef PtrToNode Stack;

int IsEmpty(Stack S);
Stack CreateStack(void);
void DisposeStack(Stack S);
void MakeEmpty(Stack S);
void Push(ElementType X, Stack S);
ElementType Top(Stack S);
void Pop(Stack S);

#endif    /*_Stack_h*/

struct Node
{
    ElementType Element;
    PtrToNode Next;
};

        创建一个空栈也很简单，我们只要创建一个头节点，MakeEmpty设置Next指针指向NULL(见图3-41)。Push是通过向链表前端进行插入而实现的，其中，表的前端作为栈顶(见图3-42)。Top的实现是通过检查表在第一个位置上的元素而完成的(见图3-43)。最后，Pop是通过删除表的前端的元素而实现的(见图3-44)。

int IsEmpty(Stack S)
{
    return S->Next == NULL;
}

Stack CreateStack(void)
{
    Stack S;

    S = malloc(sizeof(struct  Node));
    if (S == NULL)
        FatalError("Out of space!!!");
    S->Next == NULL;
    MakeEmpty(S);
    return S;
}

void MakeEmpty(Stack S)
{
    if (S == NULL)
        Error("Must use CreateStack first");
    else
        while (!IsEmpty(S))
            Pop(S);
}

void Push(ElementType X, Stack S)
{
    PtrToNode TmpCell;

    TmpCell = malloc(sizeof(struct Node));
    if (TmpCell == NULL)
        FatalError("Out of space!!!");
    else
    {
        TmpCell->Element = X;
        TmpCell->Next = S->Next;
        S->Next = TmpCell;
    }
}

ElementType Top(Stack S)
{
    if (!IsEmpty(S))
        return S->Next->Element;
    Error("Empty stack");
    return 0;
}

void Pop(Stack S)
{
    PtrToNode FirstCell;

    if (IsEmpty(S))
        Error("Empty stack");
    else
    {
        FirstCell = S->Next;
        S->Next = S->Next->Next;
        free(FirstCell);
    }
}

        所有的操作均花费常数时间，因为这些例程没有任何地方涉及栈的大小(空栈除外)，更不用说依赖于栈大小的循环了。这种实现方法的缺点在于对malloc和free的调用的开销是昂贵的，特别是与指针操作的例程相比。有的缺点通过使用第二个栈可以避免，第二个栈初始时为空栈。当一个单元从第一个栈弹出时，它只是被放到了第二个栈中。此后，当第一个栈需要新的单元时，它首先去检查第二个栈。

2.栈的数组实现

        另一种实现方法避免了指针并且可能是更流行的解决方案。这种策略的唯一潜在危害是我们需要提前声明一个数组的大小。一般说来，这并不是问题，因为在典型的应用程序中，即使有相当多的栈操作，在任意时刻栈元素的实际个数从不会太大。声明一个数组足够大而不至于浪费太多的空间通常并没有什么困难。如果不能做到这一点，那么节省的做法是使用链表来实现。
        用一个数组实现栈是很简单的。每一个栈有一个TopOfStack，对于空栈它是一1(这就是空栈的初始化)。为了将某个元素X压入该栈，我们将Topofstack加1，然后置Stack[ropofstack]=X，其中 Stack是代表具体栈的数组。为了弹出栈元素，我们置返回值为Stack[TopofStack]然后Topofstack减1。由于潜在地存在多个栈，因此Stack数组和TopofStack只代表一个栈结构的一部分。使用全局变量和固定名字来表示这种(或任意)数据结构非常不好，因为在大多数实际情况下总是存在多个栈。当编写实际程序的时候，你应该尽可能严格地遵循模型，这样，除一些栈例程外，你的程序的任何部分都没有存取被每个栈蕴含的数组或栈顶(top-of-stack)变量的可能。这对所有的ADT操作都是成立的。像Ada和C++这样的现代程序设计语言实际上都能够实施这个法则。
        注意，这些操作不仅以常数时间运行，而且是以非常快的常数时间运行。在某些机器上，若在带有自增和自减寻址功能的寄存器上操作，则(整数的)Push和Pop都可以写成一条机器指令。最现代化的计算机将栈操作作为它的指令系统的一部分，这个事实强化了这样一种观念，即栈很可能是计算机科学中仅次于数组的最基本的数据结构。
        一个影响栈的执行效率的问题是错误检测。链表实现仔细地检查错误。正如上面所描述的，对空栈的Pop或者对满栈的Push都将超出数组的界限并引起程序崩溃。显然，我们不愿意出现这种情况。但是，如果把对这些条件的检测放到数组实现过程中，那就很可能要花费像实际栈操作那样多的时间。由于这个原因，除非在错误处理极其重要的场合(如在操作系统中)，一般在栈例程中省去错误检测就成了惯用手法。虽然在多数情况下可能通过声明一个栈大到不至于使得操作溢出，并保证使用Pop操作的例程绝不对一个空栈执行Pop而侥幸避免对错误的检测，但是，这充其量只不过是使得程序得以正常运行而已，特别是当程序很大并且是由不止一个人编写或分若干次写成的时候。因为栈操作花费如此快的常数时间，所以一个程序的主要运行时间很少会花在这些例程上面。这就意味着，忽略错误检测一般是不妥的。你应该随时编写错误检测的代码；如果它们冗长，那么当它们确实耗费太多时间时你总可以将它们去掉。

        在图3-45中Stack(栈)定义为指向一个结构体的指针。该结构体包含TopofStack域和Capacity域。一旦知道最大容量，则该栈即可被动态地确定。图3-46创建了一个具有给定的最大值的栈。第3～5行指定该栈的结构，而第6～8行则指定栈的数组。第9行和第10行初始化域TopofStack和域Capacity。栈的数组不需要初始化。第11行返回栈。

#ifndef _Stack_h

struct StackRecord;
typedef struct StackRecord *Stack;

int IsEmpty(Stack S);
int IsFull(Stack S);
Stack CreateStack(int MaxElements);
void DisposeStack(Stack S);
void MakeEmpty(Stack S);
void Push(ElementType X, Stack S);
ElementType Top(Stack S);
void Pop(Stack S);
ElementType TopAndPop(Stack S);

#endif  /*_Stack_h*/

#define EmptyTOS (-1)
#define MinStackSize (5)

struct StackRecord
{
    int Capacity;
    int TopOfStack;
    ElementType *Array;
};

Stack CreateStack(int MaxElements)
{
    Stack S;

    if (MaxElements < MinStackSize)
        Error("Stack size is too small");

    S = malloc(sizeof(struct StackRecord));
    if (S == NULL)
        FatalError("Out of space!!!");

    S->Array = malloc(sizeof(ElementType) * MaxElements);
    if (S->Array == NULL)
        FatalError("Out of space!!!");
    S->Capacity = MaxElements;
    MakeEmpty(S);

    return S; 
}

        为了释放栈结构体应该编写例程DisposeStack。这个例程首先释放栈数组，然后释
放栈结构体(见图3-47)。由于CreateStack在栈的数组实现中需要一个参数，而在链表实现中不需要参数，因此若在后者的实现中不添要知道正在使用的是哪种实现方法。不幸的是，效率和软件理想主义常常发生冲突。
        我们已经假设所有的栈均处理相同类型的元素。在许多编程语言中，如果存在不同类型的栈，那么我们就需要为每种不同类型的栈重新编写一套栈的新例程，同时给每套例程赋予不同的名字。在C++中提供了更彻底的方法，它允许我们编写一套一般的栈例程，对任何类型的栈都能正常运行。C++还允许几种不同类型的栈保留相同的过程和函数名(如Push和Pop)，通过检验主调例程的类型，编译程序可决定使用哪些例程。
        在进行了上面的阐述以后，现在我们就来重写五个栈例程。我们将以纯ADT风格使函数和过程的标题等同于链表实现。这些例程本身(见图3-48到图3-52)。

void DisposeStack(Stack S)
{
    if (S != NULL)
    {
        free(S->Array);
        free(S);
    }
}

int IsEmpty(Stack S)
{
    return S->TopOfStack == EmptyTOS;
}

void MakeEmpty(Stack S)
{
    S->TopOfStack = EmptyTOS;
}

void Push(ElementType X, Stack S)
{
    if (IsFull(S))
        Error("Full stack");
    else
        S->Array[++S->TopOfStack] = X;
}

ElementType Top(Stack S)
{
    if (!IsEmpty(S))
        return S->Array[S->TopOfStack];
    Error("Empty stack");
    return 0;
}

void Pop(Stack S)
{
    if (IsEmpty(S))
        Error("Empty stack");
    else
        S->TopOfStack--;
}

        Pop偶尔写成返回弹出的元素(并使栈改变)的函数。虽然当前的想法是函数不应该改
变其输入参数，但是图3-53表明这在C中是最方便的方法。 

ElementType TopAndPop(Stack S)
{
    if (!IsEmpty(S))
        return S->Array[S->TopOfStack--];
    Error("Empty stack");
    return 0;
}

3.3.3 应用

        毫不奇怪，如果我们把操作限制于一个表，那么这些操作会执行得很快。然而，令人惊奇的是，这些少量的操作非常强大和重要。在栈的许多应用中，我们给出三个例子，第三个实例深刻说明程序是如何组织的。

1.平衡符号

        编译器检查程序的语法错误，但是常常由于缺少一个符号(如遗漏一个花括号或注释起始符)引起编译器列出上百行的诊断，而真正的错误并没有找出。
        在这种情况下，可以使用一个程序来检验是否每个符号都成对出现。于是，每一个右花括号、右方括号及右圆括号必然对应其相应的左括号。序列“[ ( ) ]”是合法的，但“[ ( ] )”是错误的。显然，不值得为此编写一个大型程序，事实上检验这些事情是很容易的。为简单起见，我们仅就圆括号、方括号和花括号进行检验并忽略出现的任何其他字符。
        这个简单的算法用到一个栈，叙述如下：
        做一个空栈。读入字符直到文件尾。如果字符是一个开放符号，则将其推入栈中。如果字符是一个封闭符号，则当栈空时报错；否则，将栈元素弹出。如果弹出的符号不是对应的开放符号，则报错。在文件尾，如果栈非空则报错。
        你应该能够确信这个算法是会正确运行的。很清楚，它是线性的，事实上它只需对输入进行一趟检验。因此，它是在线(on-line)的，是相当快的。当报错时，决定如何处理需71 要做一些附加的工作——例如判断可能的原因。

2.后缀表达式

        假设我们有一个便携计算器并想要计算一趟外出购物的花费。为此，我们将一列数据相加并将结果乘以1.06——它们是所购物品的价格以及附加的地方税。如果购物各项花销
为4.99、5.99和6.99，那么输入这些数据的自然的方式将是
        4.99+5.99+6.99 * 1.06=
        随着计算器的不同，这个结果或者是所要的答案19.05，或者是科学答案18.39。最简单的四功能计算器将给出第一个答案，但是许多先进的计算器是知道乘法的优先级是高于加法的。
        另一方面，有些项是需要上税的而有些项则不需要，因此，如果只有第一项和最后一项是要上税的，那么
        4.99 * 1.06+5.99+6.99 * 1.06=
将在科学计算器上给出正确的答案(18.69)而在简单计算器上给出错误的答案(19.37)。科学计算器一般包含括号，因此我们总可以通过加括号的方法得到正确的答案，但是使用简单计算器则需要记住中间结果。
        该例的典型计算顺序可以是将4.99和1.06相乘并存为，然后将5.99和相加，再将结果存入。我们再将6.99和1.06相乘并将答案存为，最后将和。相加并将最后结果放入。我们可以将这种操作顺序书写如下：
        4.99 1.06 * 5.99+6.99 1.06 * +
        这个记法叫作后缀(postfix)或逆波兰(reverse Polish)记法，其求值过程恰好就是我们上面所描述的过程。计算这个问题最容易的方法是使用一个栈。当见到一个数时就把它推入栈中；在遇到一个运算符时该算符就作用于从该栈弹出的两个数(符号)上，将所得结果推入栈中。例如，后缀表达式
6 5 2 3+8 * +3+ *
计算如下：前四个字符放入栈中，此时栈变成

下面读到一个“+”号，所以3和2从栈中弹出，并将它们的和5压入栈中。

接着，8进栈。

现在见到一个“*”号，因此8和5弹出，并且5 * 8=40进栈

 接着又见到一个“+”号，因此40和5被弹出，并且5+40=45进栈。

现在将3压入栈中。

然后“+”使得3和45从栈中被弹出，并将45+3=48压入栈中。

最后，遇到一个“*” 号，从栈中弹出48和6，将结果6*48=288压入栈中。

        计算一个后缀表达式花费的时间是，因为对输入中的每个元素的处理都是由一些栈操作组成从而花费常数时间。该算法的计算是非常简单的。注意，当一个表达式以后缀记号给出时，没有必要知道任何优先规则。这是一个明显的优点。

3.中缀到后缀的转换

        栈不仅可以用来计算后缀表达式的值，而且我们还可以用栈将一个标准形式的表达式(或叫作中缀式(infix))转换成后缀式。我们通过只允许操作+、* 、( 、)，并坚持普通的优先级法则而将一般的问题浓缩成小规模的问题。我们还要进一步假设表达式是合法的。假设我们欲将中缀表达式
        a+b * c+(d * e+f) * g

转换成后缀表达式。正确的答案是
        a b c * +d e * f+g * +
        当读到一个操作数的时候，立即把它放到输出中。操作符不立即输出，所以必须先存在某个地方。正确的做法是将已经见到过的操作符放进栈中而不是放到输出中。当遇到左圆括号时我们也要将其推入栈中。我们从一个空栈开始计算。
        如果见到一个右括号，那么就将栈元素弹出，将弹出的符号写出直到我们遇到一个(对应的)左括号，但是这个左括号只被弹出，并不输出。
        如果见到任何其他的符号( “+”  “*”  “(” )，那么我们从栈中弹出栈元素直到发现优先级更低的元素为止。有一个例外：除非是在处理一个“)”的时候，否则我们绝不从栈中移走“(”。对于这种操作，“+”的优先级最低，而“(”的优先级最高。当从栈弹出元素的工作完成后，我们再将操作符压入栈中。
        最后，如果读到输入的末尾，我们将栈元素弹出直到该栈变成空栈，将符号写到输出中。
        为了理解这种算法的运行机制，我们将把上面的中缀表达式转换成后缀形式。首先，读入a，于是将它输出。然后，读入“+”并放入栈中。接着是读入b并输出。这一时刻的状态如下：

这时读入“*”。操作符栈的栈顶元素比“*”的优先级低，故没有输出，“*”进栈。接着，将c读入并输出。至此，我们有

后面的符号是一个“+”。检查一下栈，我们发现，需要将“*”从栈弹出并放到输出中；弹出栈中剩下的“+”，该操作符不比刚刚遇到的符号“+”优先级低，而是有相同的优先级；然后，将刚刚遇到的“+”压入栈中。

下一个读入的符号是一个“(”，由于有最高的优先级，因此将它放进栈中。然后，将d读入并输出。

继续进行，我们又读到一个“*”。除非正在处理闭括号，否则开括号不会从栈中弹出，因此没有输出。下一个是e，将它读入并输出。

再往后读到的符号是“+”。我们将“*”弹出并输出，然后将“+”压入栈中。之后，我
们读到f并输出。

现在，我们读到一个“)”，因此将在“(”之上的栈元素弹出，这里将一个“+”号输出。

下面又读到一个“*”，将该算符压入栈中。然后，将g读入并输出。

现在输入为空，因此我们将栈中的符号全部弹出并输出，直到栈变成空栈。

        与前面相同，这种转换只需要时间并经过一趟输入后运算即可完成。我们可以通
过指定减法和加法有相同的优先级以及乘法和除法有相同的优先级而将减法和除法添加到指令集中。一种巧妙的想法是将表达式“a-b-c”转换成“ab-c-”而不是转换成“abc--”。我们的算法做了正确的工作，因为这些操作符是从左到右结合的。一般情况未必如此，比如下面的表达式就是从右到左结合的：，而不是。我们将把取幂运算添加到指令集中的问题留作练习。

4.函数调用

        检测平衡符号的算法提供一种实现函数调用的方法。这里的问题是，当调用一个新函数时，主调例程的所有局部变量需要由系统存储起来，否则被调用的新函数将会覆盖调用例程的变量。不仅如此，该主调例程的当前位置必须要存储，以便在新函数运行完后知道向哪里转移。这些变量一般由编译器指派给机器的寄存器，但存在某些冲突(通常所有的过程都将某些变量指派给1号寄存器)，特别是涉及递归的时候。该问题类似于平衡符号的原因在于，函数调用和函数返回基本上类似于开括号和闭括号，二者想法是一样的。
        当存在函数调用的时候，需要存储的所有重要信息，诸如寄存器的值(对应变量的名字)和返回地址(它可从程序计数器得到，典型情况下计数器就是一个寄存器)等，都要以抽象的方式存在“一张纸上”并被置于一个堆(pile)的顶部。然后控制转移到新函数，该函数自由地用它的一些值代替这些寄存器。如果它又进行其他的函数调用，那么它也遵循相同的过程。当该函数要返回时，它查看堆顶部的那张“纸”并复原所有的寄存器。然后它进行返回转移。
        显然，所有工作均可由一个栈来完成，而这正是在实现递归的每一种程序设计语言中实际发生的事实。所存储的信息或称为活动记录(activation record)，或叫作栈帧(stackframe)。在典型情况下，需要做些微调：当前环境是由栈顶描述的。因此，一条返回语句就可给出前面的环境(不用复制)。在实际计算机中的栈常常是从内存分区的高端向下增长，而在许多的系统中是不检测溢出的。由于有太多同时在运行着的函数，用尽栈空间的情况总是可能发生的。显而易见，用尽栈空间通常是致命的错误。
        在不进行栈溢出检测的语言和系统中，程序将会崩溃而没有明显的说明。在这些系统中，当你的栈太大时会发生一些奇怪的事情，因为它可能波及部分程序。这部分也许是主程序，也许是数据部分，特别是当使用大的数组的时候。如果主程序发生栈溢出，那么程序就会出现讹误，产生一些无意义的指令并在这些指令被执行时程序崩溃。如果数据部分发生栈溢出，很可能发生的是：当你将一些信息写入你的数据时，这些信息将冲毁栈的信息(很可能是返回地址)，那么你的程序将返回到某个奇怪的地址上去，从而程序崩溃。
        在正常情况下不应该越出栈空间，发生这种情况通常是由失控递归(忘记基准情形)的指向引起的。另一方面，某些完全合法并且表面上无害的程序也可以使你越出栈空间。图3-54中的例程打印一个链表，该例程完全合法，实际上是正确的。它正常地处理空表的基准情形，并且递归也没问题。可以证明这个程序是正确的。但是不幸的是，如果这个链表含有20000个元素，那么就有表示第3行嵌套调用20000个活动记录的一个栈。典型的情况是这些活动记录由于它们包含全部信息而特别庞大，因此这个程序很可能要越出栈空间。(如果20 000个元素还不足以使程序崩溃，那么可用更大的个数代替它。)

void PrintList(List L)
{
    if (L != NULL)
    {
        PrintElment(L->Element);
        PrintList(L->Next);
    }
}

        这个程序称为尾递归(tail recursion)，是使用递归极端不当的例子。尾递归指的是在最后一行的递归调用。尾递归可以通过将递归调用变成goto语句并在其前加上对函数每个参数的赋值语句而手工消除。它模拟了递归调用，因为没有什么需要存储，在递归调用结束之后，实际上没有必要知道存储的值。因此，我们就可以带着在一次递归调用中已经用过的那些值跳转到函数的顶部。图3-55显示改进图3-54后的程序。记住，你应该使用更自然的while循环结构。此处使用goto是为了说明编译器如何自动地去除递归。

        尾递归的去除是如此简单，以致某些编译器能够自动地完成。但是即使如此，最好还是你的程序中别这样用。

        递归总能被彻底除去(编译器是在转变成汇编语言时完成的)，但是这么做是相当冗长乏味的。一般方法是要求使用一个栈，而且仅当你能够把栈的大小限制在最低限度时，这个方法才值得一用。我们将不对此做进一步的详细讨论，只是指出，虽然非递归程序一般说来确实比等价的递归程序要快，但是速度优势的代价却是由于去除递归而使得程序清晰性变得不足。

void PrintList(List L)
{
    top:
        if (L != NULL)
        {
            PrintElement(L->Element);
            L = L->Next;
            goto top;
        }
}