【代码随想录】第6章:字符串
字符串
在C语言中,把一个字符串存入一个数组时,也把结束符 '\0’存入数组,并以此作为该字符串是否结束的标志。
string str = "abc";
for (int i = 0; str[i] != '\0'; i++) {
cout << str[i] << endl;
}
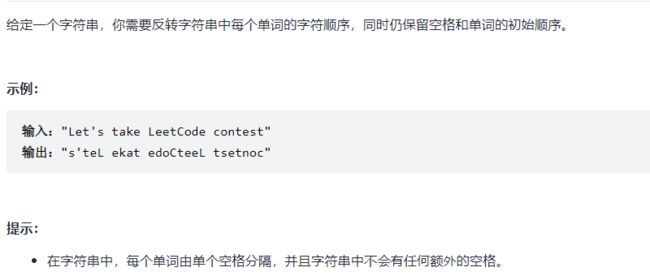
反转字符串
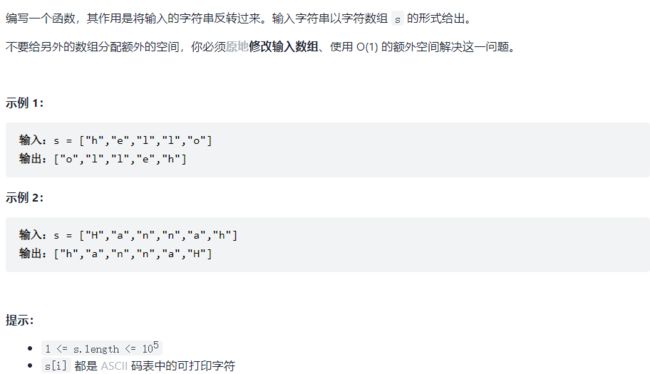
344. 反转字符串【简单】
非常简单
题目意思:实现库函数reverse的功能
思路1:遍历数组,交换前后
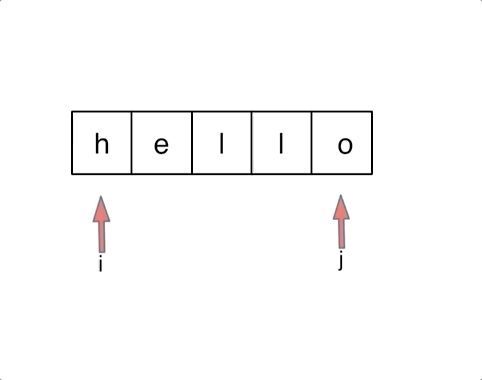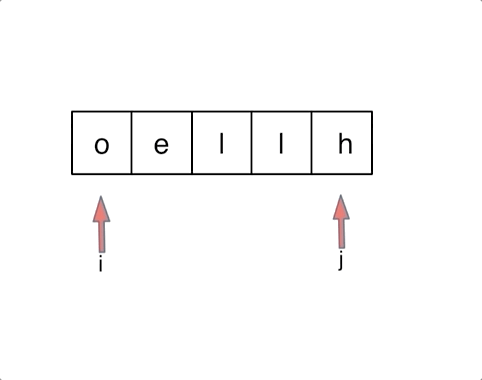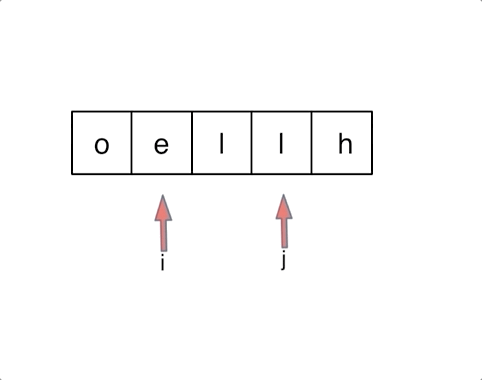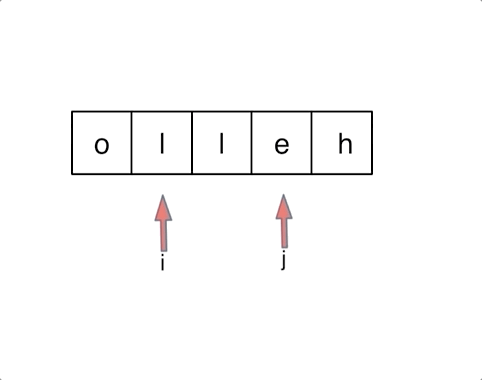
思路2:首尾指针实现交换
class Solution {
public:
void reverseString(vector& s) {
for (int i = 0; i < s.size() / 2; i++) {
swap(s[i], s[s.size() - i - 1]);
}
}
};
class Solution {
public:
void reverseString(vector& s) {
for (int i = 0, j = s.size() - 1; i < j; i++, j--) {
swap(s[i],s[j]);
}
}
};
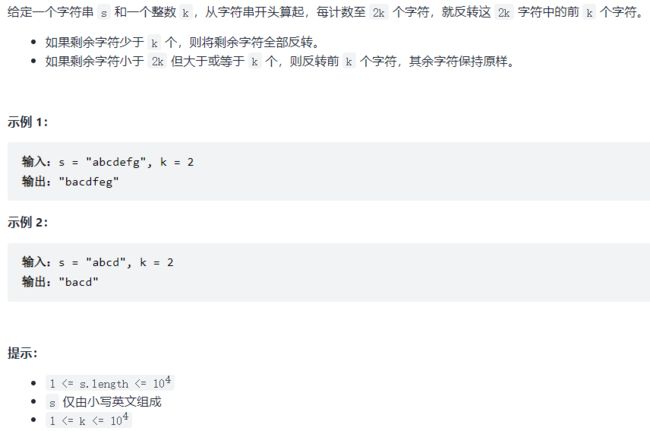
541. 反转字符串 II【简单】
思路一:使用reverse函数
class Solution {
public:
string reverseStr(string s, int k) {
for (int i = 0; i < s.size(); i += (2 * k)) {
// 1. 每隔 2k 个字符的前 k 个字符进行反转
// 2. 剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符
if (i + k <= s.size()) {
reverse(s.begin() + i, s.begin() + i + k);
}
else {
// 3. 剩余字符少于 k 个,则将剩余字符全部反转。
reverse(s.begin() + i, s.end());
}
}
return s;
}
};
思路二:自写reverse函数
class Solution {
public:
void reverse(string& s, int start, int end) {
for (int i = start, j = end; i < j; i++, j--) {
swap(s[i], s[j]);
}
}
string reverseStr(string s, int k) {
for (int i = 0; i < s.size(); i += (2 * k)) {
if (i + k <= s.size()) {
reverse(s, i, i + k - 1);
}
else {
reverse(s, i, s.size() - 1);
}
}
return s;
}
};
替换字符
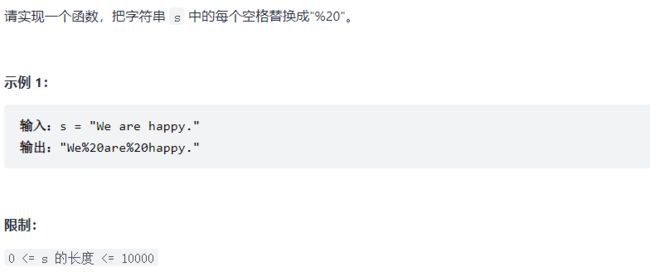
剑指 Offer 05. 替换空格【简单,双指针】
思路一:使用额外辅助空间;重新生成一条字符串,不是空格就正常拼接字符串,是空格就拼接%20
时间复杂度:O(n)
空间复杂度:O(n)
思路二:不使用辅助空间
双指针实现;需要先扩容
时间复杂度:O(n)
空间复杂度:O(1)
class Solution {
public:
string replaceSpace(string s) {
int count = 0; // 1.统计空格的个数
int sOldSize = s.size();
for (int i = 0; i < s.size(); i++) {
if (s[i] == ' ') {
count++;
}
}
// 2. 扩充字符串s的大小,也就是每个空格替换成"%20"之后的大小
s.resize(s.size() + count * 2);
int sNewSize = s.size();
// 3. 0从后先前将空格替换为"%20"
for (int i = sNewSize - 1, j = sOldSize - 1; j < i; i--, j--) {
if (s[j] != ' ') {
s[i] = s[j];
} else {
s[i] = '0';
s[i - 1] = '2';
s[i - 2] = '%';
i -= 2;
}
}
return s;
}
};
反转字符串里的单词
557. 反转字符串中的单词 III【简单】
思路一:使用额外容器
时间复杂度:O(n)
空间复杂度:O(n)
class Solution { //这个竟然没想到
public:
string reverseWords(string s) {
string ret;
int length = s.length();
int i = 0;
while (i < length) {
int start = i;
while (i < length && s[i] != ' ') { //1.定位到每个单词的尾字母的索引
i++;
}
for (int p = start; p < i; p++) {
ret.push_back(s[start + i - 1 - p]); //2.倒着添加单词
}
while (i < length && s[i] == ' ') { //3.添加空格
i++;
ret.push_back(' ');
}
}
return ret;
}
};
思路二:原地解法;双指针
时间复杂度:O(n)
空间复杂度:O(1)
class Solution {
public:
void reverse(string& s, int start, int end) {
for (start, end; start < end; start++, end--) {
swap(s[start], s[end]);
}
}
string reverseWords(string s) {
int n = s.size();
int slow = 0;
int fast = 0;
for (fast; fast < n; fast++) {
if (fast == n - 1) { //处理最末尾一个单词
reverse(s, slow, fast);
}
if (s[fast] == ' ') {
reverse(s, slow, fast - 1);
slow = fast + 1;
}
}
return s;
}
};
151. 翻转字符串里的单词【简单】
原地解法思路:
1.先去掉所有冗余空格
2.再整体反转字符串
3.再一个一个单词反转
步骤一种去空格我们不能用erase,因为erase的复杂度为O(n)
主要是明白上面的做题思路,还有会实现去空格的方法
class Solution {
public:
//函数一:反转字符串s中左闭又闭的区间[start, end]
void reverse(string& s, int start, int end) {
for (int i = start, j = end; i < j; i++, j--) { //首尾指针实现
swap(s[i], s[j]);
}
}
//函数二:移除冗余空格:使用双指针(快慢指针法)O(n)的算法
void removeExtraSpaces(string& s) {
int slow = 0, fast = 0; // 定义快指针,慢指针
for (fast; fast < s.size(); fast++) { //生成无多余空格的新字符串
if (s[fast] != ' ') {
s[slow] = s[fast];
slow++;
}
else if (fast - 1 >= 0 && s[fast - 1] != ' ' && s[fast] == ' ') {
s[slow] = ' ';
slow++;
}
}
if (slow - 1 > 0 && s[slow - 1] == ' ') { //检查字符串最末尾是不是空格
s.resize(slow - 1);
}
else {
s.resize(slow);
}
}
string reverseWords(string s) {
removeExtraSpaces(s); // 1.去掉冗余空格
reverse(s, 0, s.size() - 1); // 2.将字符串全部反转
int slow = 0;
int fast = 0;
for (fast; fast < s.size(); fast++) { //3.再反转各个单词
if (fast == s.size() - 1) { //处理最末尾一个单词
reverse(s, slow, fast);
return s;
}
if (s[fast] == ' ') {
reverse(s, slow, fast - 1);
slow = fast + 1;
}
}
return s;
}
};
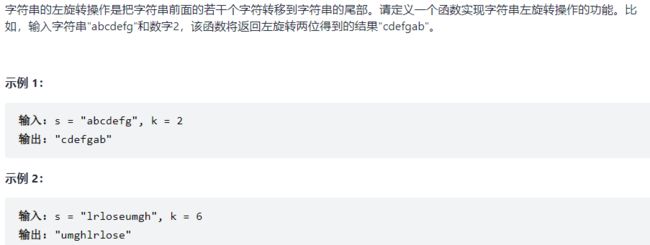
左旋字符串
剑指 Offer 58 - II. 左旋转字符串【简单,三次翻转】
思路一:使用多余容器,遍历字符串
class Solution {
public:
string reverseLeftWords(string s, int n) {
string res;
for (int i = 0; i < s.size(); i++) {
res += s[(i + n) % s.size()];
}
return res;
}
};
当然也可以用substr函数来做这种题,时间复杂度都是O(n),但是使用了多余容器,即空间复杂度也为O(n)
这题思路很重要!!!
思路二:原地解法:三次翻转
class Solution {
public:
string reverseLeftWords(string s, int n) {
reverse(s.begin(), s.end()); //第一次翻转:整体翻转
reverse(s.begin(), s.begin() + s.size() - n); //第二次翻转,翻转前半部分
reverse(s.begin() + s.size() - n, s.end());//第三次翻转,翻转后半段
return s;
}
};
此题思路与189. 轮转数组一样,不同的是一个数组一个字符串
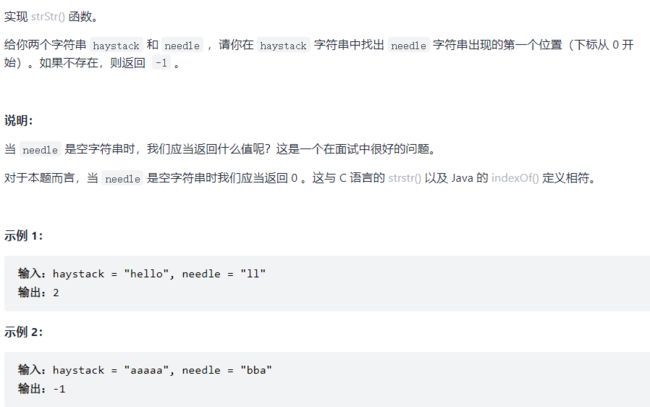
KMP算法
28. 实现 strStr()【简单,KMP】
思路一:BF法,即朴素匹配,暴力破解
时间复杂度:O(nm)
空间复杂度:O(1)
class Solution {
public:
int strStr(string haystack, string needle) {
if (needle.size() > haystack.size()) return -1; //排除子串比主串长的情况
if (needle.size() == 0) return 0; //排除子串为空串的情况
int i = 0, j = 0;
while (i < haystack.size() && j < needle.size()) {
if (haystack[i] == needle[j]) { //1.两字符相等则继续匹配
i++;
j++;
}
else { //主串起始位置右移,子串置位
i = i - j + 1; //移动一位再匹配
j = 0; //退回子串首位
}
}
if (j == needle.size()) return i - j; //2.子串中所有字符都匹配到了,就返回咯
return -1; //未匹配到
}
};
优化
//for循环比while循环性能好,主要体现在n-m上
class Solution {
public:
int strStr(string haystack, string needle) {
if (needle.size() == 0) return 0;
int n = haystack.size(), m = needle.size();
for (int i = 0; i <= n - m; i++) { //注意这里的n-m 后面有子串比主串上的情况就不需要匹配了
for (int j = 0; j < m; j++) { //遍历子串
if (haystack[i + j] != needle[j]) break;
if (j == m - 1) return i; //子串全部匹配到
}
}
return -1;
}
};
思路二:KMP算法
字符串唯一一个难的算法,重点!!!
KMP算法视频讲解:https://www.bilibili.com/video/BV1PD4y1o7nd?spm_id_from=333.999.0.0
KMP算法文档讲解:参考代码随想录
前缀表:用来回退的,它记录了子串与主串不匹配的时候,子串应该从哪里开始重新匹配
怎么制作前缀表:最长相等前后缀
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kqxmpXhf-1640348384516)(https://gitee.com/zdbya/picgo_image/raw/master/SSL_img/202112241725788.gif)]
前缀表记录的是不匹配时需要回退到哪里重新开始匹配
什么是next数组:next数组就是前缀表,但是很多实现都是把前缀表统一减1作为next数组;或者前缀表整体右移
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-j80SH6M8-1640348384516)(https://gitee.com/zdbya/picgo_image/raw/master/SSL_img/202112241730223.gif)]
时间复杂度:O(n+m)
空间复杂度:O(m),子串的长度,制作next数组
制作next数组
定义两个指针i和j,j指向前缀起始位置,i指向后缀起始位置。
统一减一版本
void getNext(int* next, const string& s){
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) { // 注意i从1开始
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j; // 将j(前缀的长度)赋给next[i]
}
}
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1XvgBV3a-1640348384517)(https://gitee.com/zdbya/picgo_image/raw/master/SSL_img/202112241751184.gif)]
不减一版本
void getNext(int* next, const string& s) {
int j = 0;
next[0] = 0;
for (int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) {
j = next[j - 1];
}
if (s[i] == s[j]) {
j++;
}
next[i] = j;
}
}
前缀表统一减一 版本
class Solution {
public:
//获取next数组的函数 统一-1版本
void getNext(int* next, const string& s) {
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) { // 注意i从1开始
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j; // 将j(前缀的长度)赋给next[i]
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) return 0; //排除特殊情况
int next[needle.size()];
getNext(next, needle); //1.获取next数组
int j = -1; // 因为next数组里记录的起始位置为-1
for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
j = next[j]; // j寻找之前匹配的位置
}
if (haystack[i] == needle[j + 1]) { // 匹配,j和i同时向后移动
j++; // i的增加在for循环里
}
if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
return (i - needle.size() + 1);
}
}
return -1;
}
};
前缀表不减一版本
背下来这个版本代码
class Solution {
public:
void getNext(int* next, const string& s) {
int j = 0;
next[0] = 0;
for(int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) {
j = next[j - 1];
}
if (s[i] == s[j]) {
j++;
}
next[i] = j;
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) return 0; //排除特殊情况
int next[needle.size()];
getNext(next, needle); //1.获取next数组
int j = 0;
for (int i = 0; i < haystack.size(); i++) {
while(j > 0 && haystack[i] != needle[j]) { // 不匹配
j = next[j - 1]; // j寻找之前匹配的位置
}
if (haystack[i] == needle[j]) { // 匹配,j和i同时向后移动
j++;
}
if (j == needle.size() ) { //子串匹配完成
return (i - needle.size() + 1);
}
}
return -1;
}
};
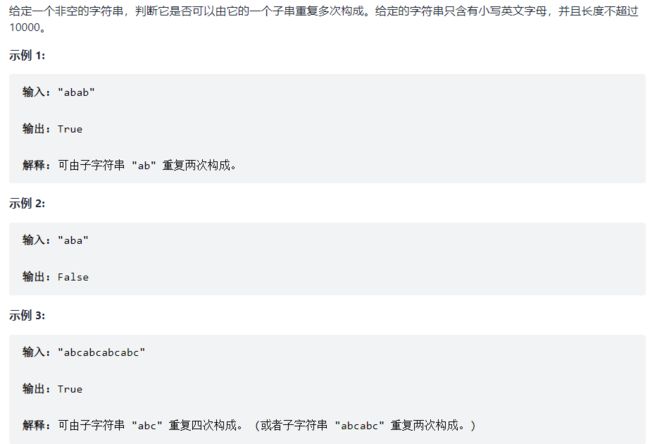
459. 重复的子字符串【简单】
方法一:暴力枚举
//时间复杂度:O(n^2)
//空间复杂度:O(1)
class Solution {
public:
bool repeatedSubstringPattern(string s) {
int n = s.size();
for (int i = 1; i <= n/2; ++i) { //枚举子串的长度
if (n % i != 0) continue; //主串的长度必须是子串长度的倍数
for (int j = i; j < n; ++j) { //遍历主串
if (s[j] != s[j % i]) { //串以i为一个周期
break;
}
if (j == n - 1) return true;
}
}
return false;
}
};
方法二:字符串查找
/*
* 双倍字符串解决;
* 从索引1开始查找
* 查找单倍字符串的位置 是否在 第二个字符串开始的位置
* 是,则 false
* 否,则 true
*/
class Solution {
public:
bool repeatedSubstringPattern(string s) {
return (s + s).find(s, 1) != s.size();
}
};
方法三:kmp实现方法二的find函数
需要掌握方法二的思路,然后用kmp做;在kmp基础上修改成这题能用的
class Solution {
public:
void getNext(int* next, const string& s) {
int j = 0;
next[0] = 0;
for (int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) {
j = next[j - 1];
}
if (s[i] == s[j]) {
j++;
}
next[i] = j;
}
}
bool kmp(string haystack, string needle) {
if (needle.size() == 0) return 0; //排除特殊情况
int next[needle.size()];
getNext(next, needle); //1.获取next数组
int j = 0;
for (int i = 1; i < haystack.size(); i++) {
while (j > 0 && haystack[i] != needle[j]) { // 不匹配
j = next[j - 1]; // j寻找之前匹配的位置
}
if (haystack[i] == needle[j]) { // 匹配,j和i同时向后移动
j++;
}
if (j == needle.size()) { //子串匹配完成
if (i == haystack.size() - 1) { //但是遍历完了主串
return false;
}
return true;
}
}
return false;
}
bool repeatedSubstringPattern(string s) {
return kmp(s + s, s);
}
};
但是这题的next数组会有一个规律
class Solution {
public:
void getNext(int* next, const string& s) {
int j = 0;
next[0] = 0;
for (int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) {
j = next[j - 1];
}
if (s[i] == s[j]) {
j++;
}
next[i] = j;
}
}
bool repeatedSubstringPattern(string s) {
if (s.size() == 0) return 0; //排除特殊情况
int next[s.size()];
getNext(next, s); //1.获取next数组
int len = s.size();
if(next[len-1] != 0 && len % (len - next[len-1]) == 0){
return true;
}
return false;
}
};
这便是最简洁的方法