【树与二叉树】堆的时间复杂度详解以及堆的应用—堆排序、TOP - K问题
![]()
个人主页:@Sherry的成长之路
学习社区:Sherry的成长之路(个人社区)
专栏链接:数据结构
长路漫漫浩浩,万事皆有期待
文章目录
- 1. 堆的时间复杂度
-
- 1.1 向下调整建堆
- 1.2 向上调整建堆
- 2. 堆的应用
-
- 2.1 堆排序
- 2.2 TOP - K问题
-
- 2.2.1 方法 1:
- 2.2.2 方法 2:
- 2.2.3 方法 3:
- I. TOP-K.h 用于函数的声明
- II. TOP-K.c 用于函数的定义
- III. Test.c 用于函数的测试
- 3.总结:
1. 堆的时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明
(时间复杂度本来看的就是近似值,多几个节点不影响最终结果)
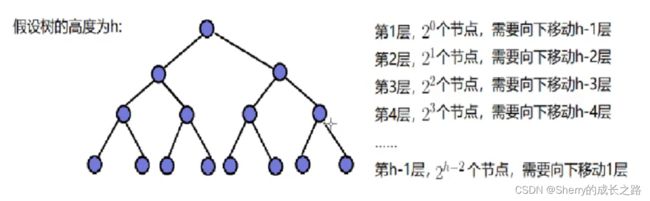
建堆的调用次数用 T(N) 表示:(从最后一个非叶子节点 <也就是倒数第二层> 开始,最坏的情况下:倒数第二层每个节点最多能向下调 1 次;倒数第三层每个节点最多能向下调 2 次;倒数第四层每个节点最多能向下调 3 次……)
1.1 向下调整建堆
每层节点个数 × 最坏情况向下调整次数:
T(N) = 2^(h-2) × 1 + 2^(h-3) × 2 + … … + 2^1 × (h-2)+2^0*(h-1)
错位相减法
等号左右两边乘个 2 得到一个新公式,再用新公式减去旧的公式,具体见下图

严格来说,向下调整的时间复杂度:N-log(N)–>O(N) [log(N)可以忽略不计]
1.2 向上调整建堆
T(N) = 2^1× 1 + 2^2× 2 + 2^3 ×3+ … … + 2^(h-3)× (h-3) + 2^(h-2) × (h-2)+ 2^(h-1) × (h-1)

综上:向下调整建堆要更优秀,效率更高

但总的来说堆排序的时间复杂度是O(N*logN)
2. 堆的应用
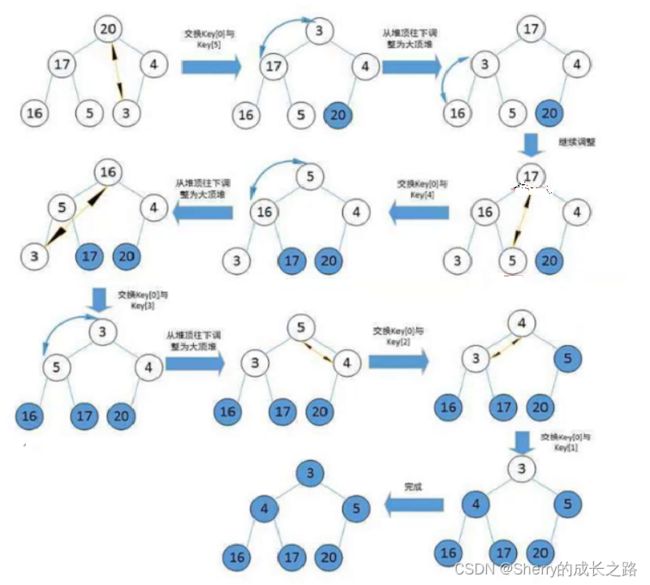
2.1 堆排序
堆创建后,如何进行排序 (升序、降序)
升序建大堆;降序建小堆。不是说升序建小堆;降序建大堆不行,而是因为不好:
如果排升序建小堆:
1、选出最小的数,最小的数就放在第一个位置
2、接着就要选次小的数,再选次小的数 … … 不断的选下去,如何选 ?
只能对剩下的 sz-1、sz-2、sz-3 … 个数继续建堆。可想这样的代价是很高的 —— 建堆的时间复杂度是 O(N),整个时间复杂度就是 O(N^2),堆的价值没有体现,不如直接循环遍历

如果排升序建大堆:
1、选出最大的数,与最后一个数交换位置
2、怎么选出次大、次次大 ?
堆的结构没有被破坏,且最后一个数不看做堆,左右子树依旧是大堆,向下调整即可
最多调整 log2N 次,整体的时间复杂度是 O(N*log2N)

对比效率:
冒泡排序和堆排序
1000 1000000
O(N2) 1000000(1百万) 1000000000000(1万亿)
O(N*log2N) 10000=10*1000 20000000(2千万)=20*1000000
向上调整建堆:模拟插入的过程
向下调整建堆:模拟删除的过程,这里从倒数的第一个非叶子节点开始调整

#include
if (arr[child] > arr[child + 1] && child + 1 < sz)
{
child++; //(当只有一个左孩子时,会越界,且后面使用时会发生非法访问)
}
//判断父亲和小孩子
//小孩子小于父亲,则交换,且继续调整 || (arr[child]>arr[parent]大孩子大于父亲,则交换,且继续调整)
if (arr[child] < arr[parent])
{
Swap(&arr[child], &arr[parent]);
//迭代
parent = child;
//重新确定左孩子的下标(当最后的叶子节点是parent时,这时去确定child会以读的方式越界,但可以不关心)
child = parent * 2 + 1;
}
//小孩子大于父亲,则停止调整
else
{
break;
}
}
}
//堆排序 -> 效率更高
void HeapSort(int* arr, int sz)
{
//建堆
int i = 0;
//从最后一棵树开始调整,也就是最后一个节点的父亲
for (i = (sz - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, sz, i);
}
}
int main()
{
//左右子树都为堆
int arr1[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
//左右子树都为非堆
int arr2[] = { 27, 37, 28, 18, 19, 34, 65, 25, 49, 15 };
HeapSort(arr1, sizeof(arr1) / sizeof(arr1[0]));
int i = 0;
for (i = 0; i < sizeof(arr1) / sizeof(arr1[0]); i++)
{
printf("%d ", arr1[i]);
}
printf("\n");
HeapSort(arr2, sizeof(arr2) / sizeof(arr2[0]));
for (i = 0; i < sizeof(arr2) / sizeof(arr2[0]); i++)
{
printf("%d ", arr2[i]);
}
return 0;
}
2.2 TOP - K问题
TOP-K问题:求数据中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:CSDN总榜前10、世界500强、未央区排名前10的泡馍等。
2.2.1 方法 1:
排序:时间复杂度 O(N * logN)
2.2.2 方法 2:
建一个 N 个数的堆(优先级队列),不断选数,选出前 K 个,时间复杂度 O(N+K * log(N))
2.2.3 方法 3:
对于 Top-K 问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆 (优化方法 ) 来解决,基本思路如下:
1 . 用数据集合中前 K 个元素来建堆
▶ 前k个最大的元素,则建小堆
▶ 前k个最小的元素,则建大堆
2.用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
▶ 将剩余 N-K 个元素依次与堆顶元素比完之后,堆中剩余的 K 个元素就是所求的前 K 个最小或者最大的元素
模拟-创建随机数种子,生成随机数
怎么知道前十个数就是 TOP - 10 ?
默认随机生成的数都是小于 1000000 的,然后给随机位置的 10 个数都是比 1000000 要大的,把这 10 个数选出来就说明算法是对的
I. TOP-K.h 用于函数的声明
#pragma once
//头
#includeII. TOP-K.c 用于函数的定义
#include"TOP-K.h"
void Swap(int* px, int* py)
{
int temp = *px;
*px = *py;
*py = temp;
}
void AdjustDown(int* arr, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (arr[child] > arr[child + 1] && child + 1 < n)
{
child++;
}
if (arr[child] < arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapPrint(HP* php)
{
assert(php);
int i = 0;
for (i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
}
printf("\n");
}
//1、对于HeapCreate函数,结构体不是外面传进来的,而是在函数内部自己malloc空间,再创建的
/*
HP* HeapCreate(HPDataType* a, int n)
{}
*/
//2、对于HeapInit函数,在外面定义一个结构体,把结构体的地址传进来
void HeapInit(HP* php, HPDataType* a, int n)
{00j000
assert(php);
//malloc空间(当前数组大小一样的空间)
php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (php->a == NULL)
{
printf("malloc fail\n");
exit(-1);
}
//使用数组初始化
memcpy(php->a, a, sizeof(HPDataType) * n);
php->size = n;
php->capacity = n;
//建堆
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(php->a, n, i);
}
}
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->size = php->capacity = 0;
}
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
void HeapPush(HP* php, HPDataType x)
{
assert(php);
//空间不够,增容
if (php->size == php->capacity)
{
HPDataType* temp = (HPDataType*)realloc(php->a, php->capacity * 2 * sizeof(HPDataType));
if (temp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
else
{
php->a = temp;
}
php->capacity *= 2;
}
//将x放在最后
php->a[php->size] = x;
php->size++;
//向上调整
AdjustUp(php->a, php->size - 1);
}
void HeapPop(HP* php)
{
assert(php);
//没有数据删除就报错
assert(!HeapEmpty(php));
//交换首尾
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
//向下调整
AdjustDown(php->a, php->size, 0);
}
HPDataType HeapTop(HP* php)
{
assert(php);
//没有数据获取就报错
assert(!HeapEmpty(php));
return php->a[0];
}
int HeapSize(HP* php)
{
assert(php);
return php->size;
}
III. Test.c 用于函数的测试
#include"TOP-K.h"
void PrintTopK(int* a, int n, int k)
{
HP hp;
HeapInit(&hp, a, k);
int i = 0;
for (i = k; i < n; i++)
{
//比较堆顶的数据
if (a[i] > HeapTop(&hp))//如果大于堆顶元素,替代进堆
{
HeapPop(&hp);
HeapPush(&hp, a[i]);
}
}
HeapPrint(&hp);
HeapDestroy(&hp);
}
void TestTopk()
{
int n = 100000;
int* a = (int*)malloc(sizeof(int)*n);
//创建随机数种子
srand((unsigned int)time(0));
//生成随机数
for (size_t i = 0; i < n; ++i)
{
a[i] = rand() % 1000000;
}
//如果找出这10个数,说明TOP-K算法是正确的
a[5] = 1000000 + 1;
a[1231] = 1000000 + 2;
a[531] = 1000000 + 3;
a[5121] = 1000000 + 4;
a[115] = 1000000 + 5;
a[2335] = 1000000 + 6;
a[9999] = 1000000 + 7;
a[76] = 1000000 + 8;
a[423] = 1000000 + 9;
a[3144] = 1000000 + 10;
PrintTopK(a, n, 10);
}
int main()
{
TestTopk();
return 0;
}
3.总结:
今天我们认识并学习了堆的时间复杂度,并且通过分析对向下调整算法和向上调整算法也有了更深入的了解。还对堆的应用——堆排序、TOP - K问题进行了分析。下一篇博客我们将对二叉树链式结构进行分析及实现。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~
![]()