耦合相似度计算度量算法（COS算法,即Coupled Object Similarity算法）的实现

最近看的论文中提到的一种解决名词性问题的相似度计算算法，叫耦合对象相似度计算方法，“COS”，注意，这里的COS不是cosine，不是余弦。况且余弦解决的数值型问题，这里说的是名词性问题相似度计算，完整的表述是（Coupled Object Similarity，即COS），完整的论文出自于Coupled nominal similarity in unsupervised learning，好像国内有个基本把人家的工作重新做了一遍还发出来的，也给一篇链接吧，毕竟做了翻译工作一种基于耦合对象相似度的项目推荐算法。

基本原理：

耦合度=内耦合*外耦合，内外耦合实际指的是属性内和属性间耦合关系，其算法不仅衡量了属性值和同样有该属性值的对象间的关系，还能够衡量这个属性和其他属性之间的关系，而关于内耦合和外耦合的具体算法，查看论文介绍，或者后续我将会补充在这篇博客下面。（其实推导过程还好，就是计算量比较大，如果手算的话，最好集中个几个小时来做，我自己花了快半个小时才算出了第一个和第二个对象之间的对象耦合相似度）

matlab编写代码：

并没有找到他的源码，于是自己编写的源码如下，解决的相似度计算问题是给出的电影矩阵，关于后面的聚类归类问题并没有做，最后给出的是相似度矩阵，该处给出的是把对象元素数字化的代码，main里面的测试数据data = [1 1 1;2 1 1;2 2 2;3 3 2;4 3 3;4 2 3];这一部分数据是论文里的数据，是为了方便计算使用的表示，在后续的对源码的更新过程中，可以对cell中的文本信息进行COS算法的计算。

如果仅仅对于代码的理解和解读，以下的代码已经足够。

function [ COS_Result ] = COS(dataMatrix,N_attr,N_obj)
%IAVAS 计算并返回耦合相似度矩阵
%   dataMatrix：原数据矩阵
%   N_attr：数据属性个数
%   N_objt：对象个数
%   objt1：第一个对象
%   objt2：第二个对象
COS_Result = zeros(N_obj,N_obj);        %初始化Ia结果矩阵
for p = 1:N_obj
    for q = 1:N_obj                     %自此构建对象关系矩阵
        %if(p ~= q)                      %考察不同对象间关系
            disp('---------------------------------');
            disp(['正在计算对象' num2str(p) '和对象' num2str(q) '间相似度...']);
            alpha = 1/(N_attr-1);       %计算α值
            res = 0;                    %记录COS值
            for i = 1:N_attr            %遍历属性
                instance1 = dataMatrix(p,i);%获取该属性下实例1的参数值
                instance2 = dataMatrix(q,i);%获取该属性下实例2的参数值
                fprintf(['  实例1值：' num2str(instance1)]);
                fprintf(['  实例2值：' num2str(instance2) '\n']);
                
                %计算内耦合
                instance1List = dataMatrix(dataMatrix(:,i) == instance1,:);%查找矩阵中第i个属性为等于instance1值的
                size1 = size(instance1List,1);
                instance2List = dataMatrix(dataMatrix(:,i) == instance2,:);
                size2 = size(instance2List,1);
                disp(['   实例1的值在该列（属性' num2str(N_attr) '）出现次数：' num2str(size1)]);
                disp(['   实例2的值在该列（属性' num2str(N_attr) '）出现次数：' num2str(size2)]);
                Ia_result = gfunc(size1,size2);
                disp(['    计算属性内耦合函数值：' num2str(Ia_result)]);
                
                %计算外耦合
                instance1 = dataMatrix(p,i);%获取实例1的参数值
                instance2 = dataMatrix(q,i);%获取实例2的参数值
                % 下面开始计算
                sum1 = 0;%用于计算求和（4.7）
                for j = 1:N_attr
                    %遍历属性
                    alpha_j = alpha;
                    if j~= i
                        % 计算公式（4.6）
                        sum2 = 0;%sum2用于计算4.6求和
                        % 先计算w集合
                        % 根据公式 w ∈ j→k(x)且?j→k(y)
                        [wjsize,wj] = wfunc(dataMatrix,i,j,instance1,instance2);%对于矩阵dataMatrix，计算w集合，x = instance1；y = instance2.
                        %wj为w集合，里面包含了wjsize个元素
                        %对每个w中的元素
                        %
                        %disp(['   输出w_j集合包含元素个数:' num2str(wjsize)]);
                        if (wjsize >=1)
                            for eachj = 1:wjsize
                                temp1 = getP(dataMatrix,i,instance1,j,wj(eachj,1));
                                temp2 = getP(dataMatrix,i,instance2,j,wj(eachj,1));
                                sum2 = sum2 + min(temp1,temp2);
                            end
                        end
                        sum1 = sum1 + alpha_j * sum2;
                    end
                end
                Ie_result = sum1;
                disp(['    计算属性外耦合函数值：' num2str(Ie_result)]);
                res = res + Ie_result*Ia_result;
            end
            disp(['COS<' num2str(p) ',' num2str(q) '>=' num2str(res)]);
            COS_Result(p,q) = res;
        %end
    end
end
end

function g = gfunc(n1,n2)   %内聚函数
g = n1*n2/(n1+n2+n1*n2);
end

function [siz,wj] = wfunc(data,k,j,i1,i2)
set1 = data(data(:,k)==i1,:);
s1 = unique(set1(:,j));
set2 = data(data(:,k)==i2,:);
s2 = unique(set2(:,j));
wj = intersect(s1,s2);
siz = size(wj,1);
if isempty(wj)
    siz = 0;
end
end

function p = getP(data,i,i1,j,i2)
l1 = data((data(:,i) == i1)&(data(:,j) == i2));
l1size = size(l1,1);
l2 = data((data(:,i) == i1));
l2size = size(l2,1);
p = l1size/l2size;
end

在调用过程使用的代码：

clc,clear all;
%新建矩阵
data = [1 1 1;...    % 表述类似于原数据中的'A1','B1','C1'
    2 1 1;...
    2 2 2;...
    3 3 2;...
    4 3 3;...
    4 2 3];
[objt,attr] = size(data);
disp(['对象个数：' num2str(objt)]);
disp(['属性个数：' num2str(attr)]);
disp('开始使用COS方法计算数据对象间的相似性...');
disp('生成对象相似度矩阵...');
disp(['大小为：' num2str(objt) '×' num2str(objt)]);
% O = 6； 6个对象
% A = 3； 3种属性
% V 类标的集合；
% V = {V1, V2, V3}；V1 = {A1，A2，A3，A4}；
%                   V2 = {B1，B2，B3}；
%                   V3 = {A1，A2，A3}；
% f 函数的集合；
% f = { f1(o1) = A1, f1(o2) = B1, f1(o3) = C1,
%      ...
%       f6(o1) = A4, f6(o2) = B2, f6(o3) = C3 }
RESULT = COS(data,attr,objt);
disp('*****输出对象关系COS结果矩阵*****');
disp(RESULT);

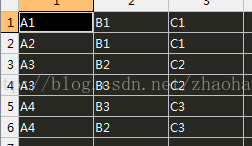
得到结果如下图：

对比main中的测试用例和上图，明显得知，1-5之间的耦合为0，对比看main中的信息，几乎找不到其耦合性，所以这个结果是正确的。

另外对于后来测试的文本型数据信息

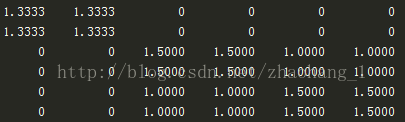
得到的结果如下图所示，

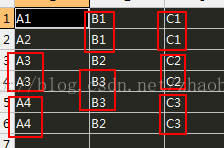
对比以下人工划分的图可知，1、2对象和3、4、5、6对象的耦合性为0，证明上式结果正确。

至此，以上即是COS对象耦合性算法代码和实验结果。