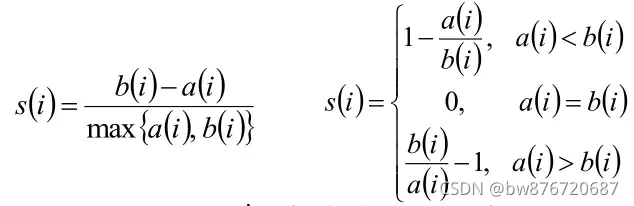机器学习——Kmeans聚类算法

简介

K均值聚类算法是先随机选取K个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

手肘法

最关键的问题是其中k值的确定方式
核心指标：SSE(sum of the squared errors，误差平方和)

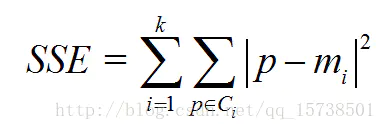
• Ci是第i个簇
• p是Ci中的样本点
• mi是Ci的质心（Ci中所有样本的均值）
• SSE是所有样本的聚类误差，代表了聚类效果的好坏。

手肘法核心思想

• 随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。

• 当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数

import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
 
df_features = pd.read_csv(r'C:\预处理后数据.csv',encoding='gbk') # 读入数据
'利用SSE选择k'
SSE = []  # 存放每次结果的误差平方和
for k in range(1,9):
    estimator = KMeans(n_clusters=k)  # 构造聚类器
    estimator.fit(df_features[['R','F','M']])
    SSE.append(estimator.inertia_) # estimator.inertia_获取聚类准则的总和
X = range(1,9)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(X,SSE,'o-')
plt.show()

轮廓系数

但是问题就出在于如何通过图像确定k值？
直接通过肉眼判断是不可信的，因此选择使用轮廓系数
使用轮廓系数(silhouette coefficient)来确定，选择使系数较大所对应的k值

方法：

• 计算样本i到同簇其他样本的平均距离ai。ai 越小，说明样本i越应该被聚类到该簇。将ai 称为样本i的簇内不相似度。
  簇C中所有样本的a i 均值称为簇C的簇不相似度。

• 计算样本i到其他某簇Cj 的所有样本的平均距离bij，称为样本i与簇Cj 的不相似度。定义为样本i的簇间不相似度：bi =min{bi1, bi2, …, bik}
  bi越大，说明样本i越不属于其他簇。

• 根据样本i的簇内不相似度a i 和簇间不相似度b i ，定义样本i的轮廓系数
  

• 判断：

• 轮廓系数范围在[-1,1]之间。该值越大，越合理。
  si接近1，则说明样本i聚类合理；
  si接近-1，则说明样本i更应该分类到另外的簇；
  若si 近似为0，则说明样本i在两个簇的边界上。

• 所有样本的s i 的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量。

• 使用轮廓系数(silhouette coefficient)来确定，选择使系数较大所对应的k值

• sklearn.metrics.silhouette_score sklearn中有对应的求轮廓系数的API

增加轮廓系数改进之后判断代码：

def cluster_para_est(train_x):
    k_num = 50
    sse = []
    for k in range(1, k_num):
        # kmeans算法
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(train_x)
        # 计算inertia簇内误差平方和
        sse.append(kmeans.inertia_)
    x = range(1, k_num)
    plt.xlabel('K')
    plt.ylabel('SSE')
    plt.plot(x, sse, 'o-')
    plt.show()
    for idx in range(len(sse) - 1):
        if sse[idx] - sse[idx + 1] <= 1:
            print(idx + 1)
            return idx + 1

代码举例1

1、便于理解，首先创建一个明显分为2类20*2的例子（每一列为一个变量共2个变量，每一行为一个样本共20个样本）：

import numpy as np
c1x=np.random.uniform(0.5,1.5,(1,10))
c1y=np.random.uniform(0.5,1.5,(1,10))
c2x=np.random.uniform(3.5,4.5,(1,10))
c2y=np.random.uniform(3.5,4.5,(1,10))
x=np.hstack((c1x,c2x))
y=np.hstack((c2y,c2y))
X=np.vstack((x,y)).T
print(X)

2、引用Python库将样本分为两类（k=2），并绘制散点图：

#只需将X修改即可进行其他聚类分析
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
 
kemans=KMeans(n_clusters=2)
result=kemans.fit_predict(X) #训练及预测
print(result)   #分类结果
 
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] #散点图标签可以显示中文
 
x=[i[0] for i in X]
y=[i[1] for i in X]
plt.scatter(x,y,c=result,marker='o')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

3、如果K值未知，可采用肘部法选择K值（假设最大分类数为9类，分别计算分类结果为1-9类的平均离差，离差的提升变化下降最抖时的值为最优聚类数K）

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
 
K=range(1,10)
meanDispersions=[]
for k in K:
    kemans=KMeans(n_clusters=k)
    kemans.fit(X)
    #计算平均离差
    m_Disp=sum(np.min(cdist(X,kemans.cluster_centers_,'euclidean'),axis=1))/X.shape[0]
    meanDispersions.append(m_Disp)
 
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] #使折线图显示中文
 
plt.plot(K,meanDispersions,'bx-')
plt.xlabel('k')
plt.ylabel('平均离差')
plt.title('用肘部方法选择K值')
plt.show()

代码举例2

文件读取的部分可以写一个独立的函数判断更加方便

import numpy as np
import matplotlib.pyplot as plt

# 加载数据
def loadDataSet(fileName):
    data = np.loadtxt(fileName,delimiter='\t')
    return data

# 欧氏距离计算
def distEclud(x,y):
    return np.sqrt(np.sum((x-y)**2))  # 计算欧氏距离

# 为给定数据集构建一个包含K个随机质心的集合
def randCent(dataSet,k):
    m,n = dataSet.shape
    centroids = np.zeros((k,n))
    for i in range(k):
        index = int(np.random.uniform(0,m)) #
        centroids[i,:] = dataSet[index,:]
    return centroids

# k均值聚类
def KMeans(dataSet,k):

    m = np.shape(dataSet)[0]  #行的数目
    # 第一列存样本属于哪一簇
    # 第二列存样本的到簇的中心点的误差
    clusterAssment = np.mat(np.zeros((m,2)))
    clusterChange = True

    # 第1步 初始化centroids
    centroids = randCent(dataSet,k)
    while clusterChange:
        clusterChange = False

        # 遍历所有的样本（行数）
        for i in range(m):
            minDist = 100000.0
            minIndex = -1

            # 遍历所有的质心
            #第2步 找出最近的质心
            for j in range(k):
                # 计算该样本到质心的欧式距离
                distance = distEclud(centroids[j,:],dataSet[i,:])
                if distance < minDist:
                    minDist = distance
                    minIndex = j
            # 第 3 步：更新每一行样本所属的簇
            if clusterAssment[i,0] != minIndex:
                clusterChange = True
                clusterAssment[i,:] = minIndex,minDist**2
        #第 4 步：更新质心
        for j in range(k):
            pointsInCluster = dataSet[np.nonzero(clusterAssment[:,0].A == j)[0]]  # 获取簇类所有的点
            centroids[j,:] = np.mean(pointsInCluster,axis=0)   # 对矩阵的行求均值

    print("Congratulations,cluster complete!")
    return centroids,clusterAssment

def showCluster(dataSet,k,centroids,clusterAssment):
    m,n = dataSet.shape
    if n != 2:
        print("数据不是二维的")
        return 1

    mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ', 'pr']
    if k > len(mark):
        print("k值太大了")
        return 1

    # 绘制所有的样本
    for i in range(m):
        markIndex = int(clusterAssment[i,0])
        plt.plot(dataSet[i,0],dataSet[i,1],mark[markIndex])

    mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', ', 'pb']
    # 绘制质心
    for i in range(k):
        plt.plot(centroids[i,0],centroids[i,1],mark[i])

    plt.show()
dataSet = loadDataSet("kk.txt")
k = 5
centroids,clusterAssment = KMeans(dataSet,k)
showCluster(dataSet,k,centroids,clusterAssment)

实例

已完成有空再整理。