Codeforces Round 910 (Div. 2)
Milica and String
题目大意:给定一个长为n的字符串s,s只包含A,B,我们现在要对字符串进行操作,要使最后字符串中恰好有k个B。我们每次操作如下:
1.选一个整数i和字符c
2.将前i个字符都换成c;
我们要找最少进行几次操作,输出并打印每次操作选择的i和c。
思路:这道题实际上与操作次数没关系,因为每次操作是将前i个全部改成c。所以我们只用先找出字符串中有多少个B,如果恰好有k个,那么就不用进行操作,如果个数小于B,那么就从头开始遍历,累计A的数量,当A的数量等于差值的时候,就可以停,并将前面的全部改成B;如果大于B,就从头开始累计B的个数,当累计的个数等于差值的时候就全部改成A。
#include
using namespace std;
int a[200];
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,m;
scanf("%d%d",&n,&m);
string s;
cin>>s;
int c=0;
for(int i=0;i Milena and Admirer
题目大意:给定一个数组a[],我们要进行若干次操作使数组变成非递减的,我们可以进行的操作如下:
选一个ai和一个数x,用x和ai-x代替ai。
问最少进行多少次操作可以实现。
思路:我们来讨论一下,非递减的话,后面一定要大于等于前面的,我们如果从前面切,后面可能会出现更小的,让前面的全部需要重切,那么我们从后面来访问的话,实际上就可以解决这个问题。然后就是怎么切的问题了,实际上可以发现,对半切是一个比较好的切法,不会让前面一半过小,但是也要注意到,对半切之后,后面的那一半可能还会大于后面的那个数,所以只切一次还不够。那么我们可不可以贴着后面的那个数来切呢,实际上也是不行的,因为可能会导致余数很小,导致前面需要切的次数增加,那么怎么切呢?尽可能地均分,均分能尽可能地保证前面的不会太小。
令j=i+1,ai>aj,按照如下的方法进行切:
切ai/aj刀,切成k=ai/aj+1块,最小的长度为ai/k;
#include
using namespace std;
#define int long long
int a[200010];
signed main()
{
int t;
scanf("%lld",&t);
while(t--)
{
int n;
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
}
int c=a[n];
int ans=0;
for(int i=n-1;i>=1;i--)
{
if(a[i]>c)
{
//切a[i]/c+1段
//余a[i]/c
int k=ceil(a[i]*1.0/c);
ans += k-1;
c=floor(a[i]*1.0/k);
}
else c=a[i];
//printf("%lld %lld\n",ans,c);
}
printf("%lld\n",ans);
}
} Colorful Grid
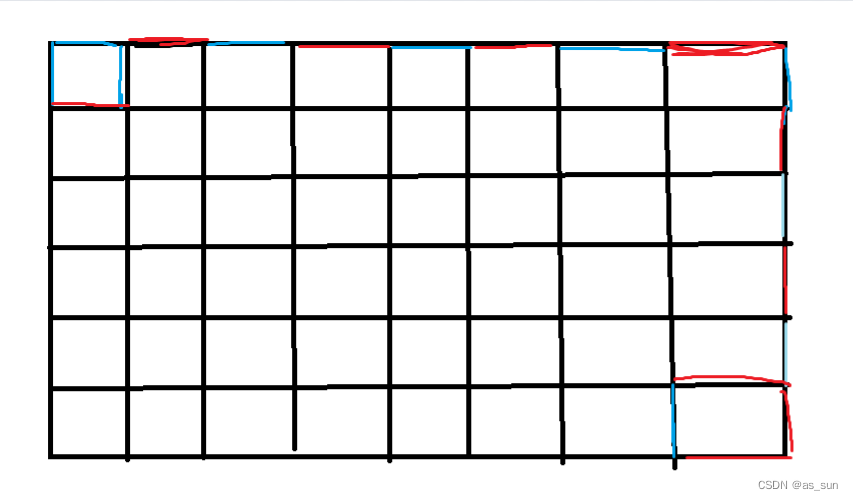
题目大意:给定一个点矩阵,一共有n行点,每行点有m个,每次操作只能从一个点到另一个点,横着或者竖着的点连起来,给边染上红色或者蓝色,每次只能沿着边走,要求是不能走连续两个相同颜色的边,只能走k步。
思路:我们从起点走到终点,不整那些花里胡哨的就是沿着上边框和有边框走,上边框包含,m-1步,右边框包含n-1步,同时这也是最近的距离,一旦可以走的步数比这个还少一定是不可以的。然后再来考虑重复路径问题:首先我们可以走到终点再绕圈,每一圈都有4步额外的,那么总步数就是n+m-2+4c;然后再考虑在路上,比如上边框的时候,我们可以先下来,横着走,再上去,那么就多了两步多余的。总步数就是n+m-2+4c+2=n+m+4c;所以(k-n-m)%4=0或2的时候是可以走的。
在路径上转圈容易使重边的计算出问题。
参考链接:CF1898 C Colorful Grid 题解 - Martian148 - 博客园 (cnblogs.com)
#include
using namespace std;
char h[20][20],s[20][20];
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,m,k;
scanf("%d%d%d",&n,&m,&k);
int d=k-(n+m-2);
int r=(k-n-m)%2;
if(d<0) printf("No\n");
else if(d>0&&r!=2&&r!=0) printf("No\n");
else
{
printf("Yes\n");
for(int i=1;i<=n;i++)
for(int j=1;j<=m-1;j++)
h[i][j]='R';
for(int i=1;i<=n-1;i++)
for(int j=1;j<=m;j++)
s[i][j]='B';
char c='R';
for(int j=1;j<=m-1;j++)
{
if(j%2) h[1][j]='B';
c=h[1][j];
}
for(int j=1;j<=n-1;j++)
{
if(c=='R') s[j][m]='B';
else s[j][m]='R';
c=s[j][m];
}
if(c=='B')
{
h[n][m-1]=h[n-1][m-1]='R';
s[n-1][m-1]='B';
}
else
{
h[n][m-1]=h[n-1][m-1]='B';
s[n-1][m-1]='R';
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m-1;j++)
{
printf("%c ",h[i][j]);
}
printf("\n");
}
for(int i=1;i<=n-1;i++)
{ for(int j=1;j<=m;j++)
printf("%c ",s[i][j]);
printf("\n");
}
}
}
} 题目大意:给定两个n长数组a[],b[],定义ans=sum(|ai-bi|),现在能对b[]中的两个数进行一次交换,问交换后ans的值最大是多少。
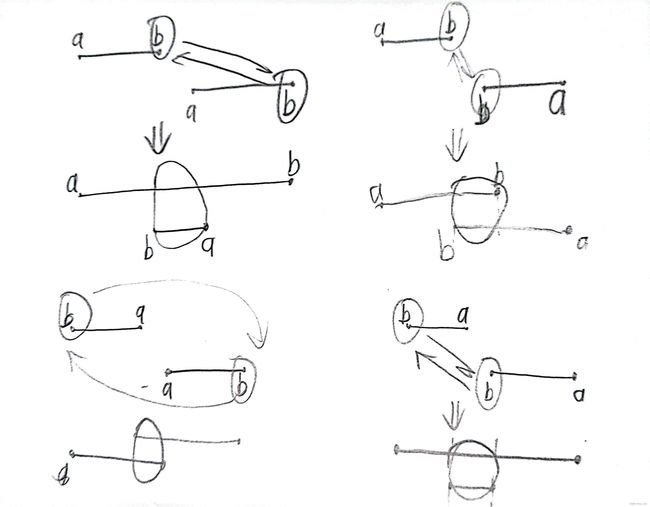
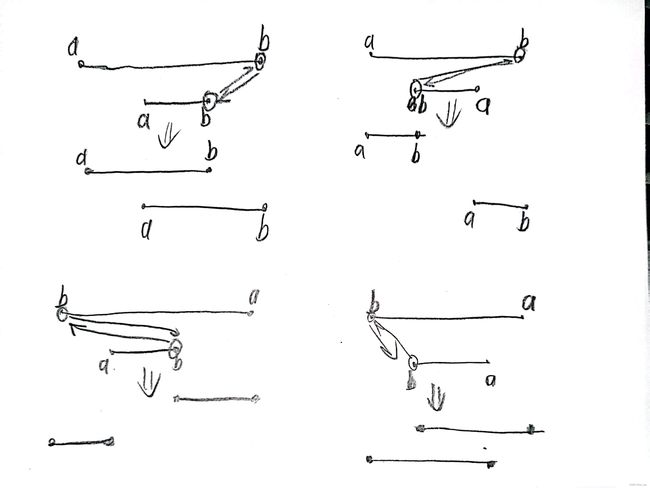
思路:这里既然取的是绝对值,那么我们就可以将之视为区间/。,而且我们只能交换一次b,那么实际上最后的落脚点是两个区间,两个区间的关系无外乎三种情况。 :不相交、相交、覆盖。我们一次对三种情况进行讨论,
1.两区间不相交
2.两区间相交
3.两区间是覆盖与被覆盖关系
由上面三种情况的讨论可知,只有当两区间不相交时,交换b才会在原来的基础上产生增益,而且增益的值为两区间间隔的二倍。所以现在的问题就转化成为了去找区间的间隔的最大值。那么要想找的区间间隔的最大值,那么就要去找所有区间右端点的最小值,和所有区间左端点的最大值,这样就能响应的找到区间间隔最大的两个区间。如果这两个区间不相交的话,那么就可以产生增益。由上面的讨论可知,左右端点是a还是b都不影响,我们关注区间的左右即可,所以又引出一个处理,在录入b的时候,如果bi#include