使用VC++实现锐化处理(使用Sobel算子、Prewitt算子、Isotropic算子)
使用VC++实现锐化处理(使用Sobel算子、Prewitt算子、Isotropic算子)
获取源工程可访问gitee可在此工程的基础上进行学习。
该工程的其他文章:
01- 一元熵值、二维熵值
02- 图像平移变换,图像缩放、图像裁剪、图像对角线镜像以及图像的旋转
03-邻域平均平滑算法、中值滤波算法、K近邻均值滤波器
04-分段线性变换,直方图均衡化、锐化处理
05-基于拉普拉斯算子、Canny的边缘检测功能、实现Otsu分割方法
06-最近邻插值,双线性插值,立方卷积插值
07-全局固定阈值分割、自适应阈值分割
08-K近邻中值滤波器(KNNMF)、最小均方差滤波器、矢量中值滤波算法
文章目录
- 使用VC++实现锐化处理(使用Sobel算子、Prewitt算子、Isotropic算子)
-
- 实验内容
- 一、Sobel算子
-
- 1.Sobel算子锐化原理
- 2.Sobel算子锐化实验代码
- 3.Sobel算子锐化现象
- 二、Prewitt算子
-
- 1.Prewitt算子锐化原理
- 2.Prewitt算子锐化实验代码
- 3.Prewitt算子锐化实验现象
- 三、Isotropic算子
-
- 1.Isotropic算子锐化原理
- 2.Isotropic算子锐化实验代码
- 3.Isotropic算子锐化实验现象
实验内容
对一幅256级灰度图像,使用VC++实现锐化处理(使用Sobel算子、Prewitt算子、Isotropic算子)。
一、Sobel算子
1.Sobel算子锐化原理
Sobel算子是一种常用于图像处理的边缘检测算子,也可用于图像锐化。其原理基于对图像的卷积操作,计算图像中每个像素点的梯度值。Sobel算子有水平方向和垂直方向两种核,分别用于检测图像中的水平和垂直边缘。
Sobel算子的水平方向卷积核:
-1 0 1
-2 0 2
-1 0 1
Sobel算子的垂直方向卷积核:
-1 -2 -1
0 0 0
1 2 1
算法步骤如下:
-
对于图像中的每个像素点,将其与Sobel算子的卷积核进行卷积操作,分别计算水平方向和垂直方向的梯度值。
-
将水平和垂直方向的梯度值合并,一般使用这两个梯度值的平方和的开根号,得到最终的梯度值。
-
将得到的梯度值映射到图像的灰度范围,例如,通过取整和截断的方式将其限定在0到255之间。
-
最终得到的图像就是经过Sobel算子锐化后的图像,边缘特征更加明显。
Sobel算子的优势在于简单易实现,对噪声具有一定的抑制作用,常用于图像边缘检测和锐化。
2.Sobel算子锐化实验代码
// 循环控制变量
int y;
int x;
CSize sizeImage = pDib->GetDimensions();
int nWidth = sizeImage.cx ;
int nHeight= sizeImage.cy ;
int templatewidth = 3;
int templateheight = 3;
int gx[100] = { 1,0,-1,
2,0,-2,
1,0,-1 };
int gy[100] = { -1,-2,-1,
0,0,0,
1,2,1 };
for (y = 1; y < nHeight - 1; y++)
for (x = 1; x < nWidth - 1; x++)
{
double Gx = 0, Gy = 0;
for(int k=0;k< templatewidth;k++)
for (int m = 0; m < templateheight; m++)
{
int gray = pDoc->m_pDibInit->GetPixelGray(x - templatewidth / 2 + m, y - templateheight / 2 + k);
Gx += gx[k * templatewidth + m] * gray;
Gy += gy[k * templatewidth + m] * gray;
}
double G_xy = sqrt(Gx * Gx + Gy * Gy); //平方和开根号
pDoc->m_pDibTest->SetPixelGray(x, y, (int)G_xy);
}
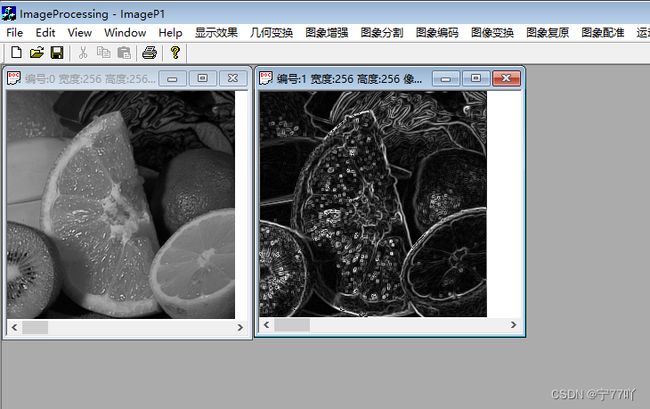
3.Sobel算子锐化现象
二、Prewitt算子
1.Prewitt算子锐化原理
Prewitt算子是一种用于图像处理的边缘检测和图像锐化的卷积算子。它类似于Sobel算子,但其权重系数略有不同。Prewitt算子有两个核,分别用于水平和垂直方向的卷积。
水平方向的Prewitt核:
-1 0 1
-1 0 1
-1 0 1
垂直方向的Prewitt核:
-1 -1 -1
0 0 0
1 1 1
Prewitt算子的原理是通过卷积计算图像中每个像素点与其周围像素的梯度,以检测图像中的边缘。具体步骤如下:
-
对图像进行灰度处理(如果图像不是灰度图)。
-
使用水平和垂直方向的Prewitt核对图像进行卷积操作,分别得到水平方向(Gx)和垂直方向(Gy)的梯度图像。
-
计算每个像素的梯度大小,通常使用以下公式:
G = G x 2 + G y 2 G = \sqrt{Gx^2 + Gy^2} G=Gx2+Gy2
-
将计算得到的梯度大小映射到新的像素值范围(例如,0到255),以生成最终的锐化图像。
Prewitt算子主要用于强调图像中的垂直或水平边缘。在图像处理中,它常被应用于边缘检测、特征提取和图像增强等任务。
2.Prewitt算子锐化实验代码
只需要在sobel算子的基础上更改两个核
//Prewitt算子
int gx[100] = { 1,0,-1,
1,0,-1,
1,0,-1 };
int gy[100] = { -1,-1,-1,
0,0,0,
1,1,1 };
3.Prewitt算子锐化实验现象
三、Isotropic算子
1.Isotropic算子锐化原理
在图像处理中,Isotropic算子是一种用于图像锐化的算子,它基于图像的梯度信息,类似于Sobel和Prewitt算子。Isotropic算子主要强调图像中的各个方向的边缘。
Isotropic算子没有固定的卷积核,而是根据图像中每个像素点周围的梯度方向进行动态调整。其原理如下:
-
计算梯度: 对图像进行梯度计算,通常使用Sobel、Prewitt或其他梯度算子。这一步会得到每个像素点的梯度强度和方向。
-
动态卷积核: 对于每个像素点,根据其梯度方向调整卷积核。通常,Isotropic算子采用一个可旋转的卷积核,可以在不同方向上产生不同的响应。这个卷积核可以根据梯度方向旋转一定的角度。
-
卷积操作: 使用动态调整后的卷积核对图像进行卷积操作。这一步产生的结果是在多个方向上对图像进行了锐化处理,以增强图像中各个方向的特征。
-
灰度映射: 将卷积操作得到的结果映射到合适的灰度范围,以生成最终的锐化图像。
Isotropic算子的优势在于它对于不同方向的边缘都有较好的响应,能够更全面地提取图像的特征。然而,由于其动态卷积核的设计,计算成本可能较高,具体实现时需要根据应用场景进行权衡。
2.Isotropic算子锐化实验代码
只需要在sobel算子的基础上更改两个核
//Isotropic算子图像锐化
// 设置模板系数
double gx[100] = { 1,0,-1,
sqrt(2),0,-sqrt(2),
1,0,-1 };
double gy[100] = { -1,-sqrt(2),-1,
0,0,0,
1,sqrt(2),1 };