C++ day52 最长递增子序列 最长连续递增子序列 最长重复子数组
题目1:300 最长递增子序列
题目链接:最长递增子序列
对题目的理解
找出整数数组中最长严格递增子序列的长度
动态规划
动规五部曲
1)dp数组及下标i的含义
dp[i]:以nums[i]为结尾的最长递增子序列的长度
递增比较的时候,如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾
2)递推公式
3)dp数组初始化
根据dp数组定义,dp[i]至少长度是1,最少包含nums[i] ,dp[i]的最大值不一定是在dp[nums.size()-1],可能出现在各个位置,因此需要遍历一遍
4)遍历顺序
求递增子序列,dp[i]依赖于前面的元素与当前数值进行比较的结果更新dp[i]的值,i从小到大遍历
for(i=1;i for(j=0;j 5)打印dp数组 代码 整数数组未经排序,找到数组中最长且连续递增的子序列,返回该序列的长度 动规五部曲 1)dp数组及下标i的含义 dp[i]:以i结尾的最长连续递增子序列的长度,注意这里只是说了以i结尾,不一定以0开始哟,注意本题的最大长度不一定是在dp[nums.szie()-1],可能出现在各个位置,所以需要遍历一遍求最大值 2)递推公式 不连续递增子序列的跟前0-i 个状态有关,连续递增的子序列只跟前一个状态有关 3)dp数组初始化 至少有1个元素,长度是1 ,dp[i]=1 4)遍历顺序 根据递推公式,i依赖于i-1,所以,从前往后遍历 for(i=1;i 5)打印dp数组 代码 返回两个整数数组中公共的且长度最长的子数组长度(子数组就是连续子序列) 动规五部曲 1)dp数组及下标i的含义 使用二维dp数组表示两个数组的所有比较情况, dp[i][j]:以i-1为结尾的nums1和以j-1为结尾的nums2的最长重复子数组的长度 注意:本题的最大长度不一定在dp[nums1.size()-1][nums2.size()-1],可能出现在各个位置,所以需要再遍历一遍,求最大值 2)递推公式 根据递推公式的定义,dp[i][j]的状态只能由dp[i-1][j-1]推导出来,if(nums1[i-1]==nums2[j-1]) dp[i][j]=dp[i-1][j-1]+1 两个数组同时回退所以只能是dp[i-1][j-1]+1,不能是dp[i][j-1]也不能是dp[i-1][j] 3)dp数组初始化 根据dp数组定义(以i-1结尾,以j-1结尾),dp[i][0]无意义状态 0-1无意义;同理,dp[0][j]无意义状态 0-1无意义,为了方便递推公式,将二者初始化为0,最长子数组长度应该从0往上加; 其他的下标的dp值初始化为任意值均可(因为计算递推公式之后会被覆盖),为了代码简洁,将dp全初始化为0 4)遍历顺序 先遍历两个数组中的哪一个都可以 for(i=1;i<=nums1.size();i++){ for(j=1;j<=nums2.size();j++)} 注意从1开始遍历(根据递推公式),且条件是小于等于,因为dp数组的定义是[i][j]代表以i-1,j-1为结尾,只有等于,才能遍历到数组中的最后一个元素,nums1.size()-1,nums2.size()-1 题目要求长度最长的子数组的长度。所以在遍历的时候顺便把dp[i][j]的最大值记录下来。 5)打印dp数组 代码 初始化简便一些 若将dp[i][j]数组定义为nums1以i结尾和nums2以j结尾,那么 第一行和第一列毕竟要进行初始化,如果nums1[i] 与 nums2[0] 相同的话,对应的 dp[i][0]就要初始为1, 因为此时最长重复子数组为1。 nums2[j] 与 nums1[0]相同的话,也是同样要把dp[0][j]初始化为1,如下图 代码 上述代码会出现如下的错误 错误的原因是即使是上面的初始化更新了dp数组,dp数组中是1,但是最终返回了result,而result又是在for循环中,两个for循环都是从1开始记录,所以整个for循环并不包括初始化的那一列,那一行进行比较,所以最终返回的结果是0 将代码更改为如下:i=0与j=0,初始化的这一行和一列还是要在for循环中进行比较的class Solution {
public:
int lengthOfLIS(vector
题目2:674 最长连续递增序列
题目链接:最长连续递增序列
对题目的理解
动态规划
class Solution {
public:
int findLengthOfLCIS(vector
贪心算法
class Solution {
public:
int findLengthOfLCIS(vector
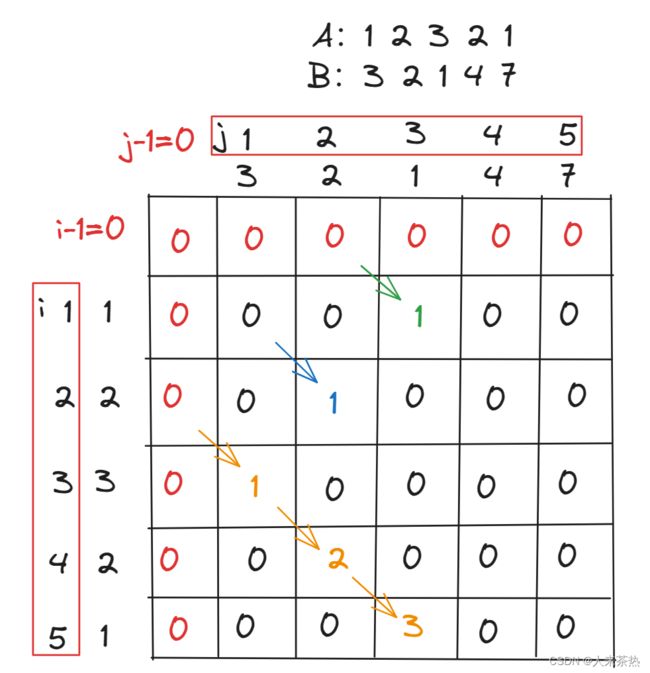
题目3:718 最长重复子数组
题目链接:最长重复子数组
对题目的理解
动态规划
class Solution {
public:
int findLength(vectorclass Solution {
public:
int findLength(vector
class Solution {
public:
int findLength(vectorclass Solution {
public:
int findLength(vector