Graph Attention Networks(GATs)

图注意网络（GATs）是对GCNs的理论改进。GATs提出了一种加权因子，该因子考虑了节点特征的“自我关注”过程，改进了GCNs静态的归一化系数。在本文中，我们将介绍GATs是如何工作的，并将其应用于实例，进一步了解其工作原理。

---

前言

在GCNs中我们就已经考虑到某些邻接节点较少的节点的重要性要高于其他节点，因此在GCNs中，我们提出了$H={\tilde{D}}^{-1}\tilde{A}X{W}^T$，但是该方法的局限性就在于它仅仅考虑了邻接节点的数量。为此，在GCNs中，我们主要利用节点特征的重要性生成相应的权重因子来改善模型的预测效果。

---

一、GATs原理

我们将权重因子成为注意力分数，并用${\alpha }_{ij}$来表示。两个节点之间的注意力分数可以用下式表示：
$$h_i=\sum _{j\in N_i}{\alpha }_{ij}W{x}_j$$
GATs的注意力分数是通过比较输入得到的，在本文中，我们将了解到如何通过以下四步来计算注意力分数，并学习如何提高GATs隐藏层的性能。

• 线性变换
• 激活函数
• Softmax归一化
• 多层注意力

1、线性变换

注意力得分代表了两个节点之间的重要性。想要计算注意力得分，我们首先需要知道隐藏层向量$W{x}_i$和$W{x}_j$。在此处，$W$在计算隐藏层向量的权重矩阵。之后，额外的线性变换应用于隐藏层向量，我们将该学习矩阵定义为$W_{att}$。在训练的过程中，$W_{att}$学习矩阵用于产生注意力系数$a_{ij}$，这一过程可以归纳为：
$$a_{ij}=W_{att}^T\left[W{x}_i\Vert W{x}_j\right]$$
线性变换的输出将作为激活函数的输入。

2、激活函数

非线性是神经网络结构中必须的一部分，而非线性的实现依赖于激活函数。典型的激活函数如图1所示。

图1 典型的激活函数

在GATs中，我们将$LeakyReLU$激活函数应用于前一步的输出。可以得到下式：
$$e_{ij}=Leaky\mathrm{Re}LU\left(a_{ij}\right)$$
在激活函数后，我们将得到的数值归一化。

3、Softmax 归一化

我们在数值归一化的基础上才可以比较不同节点的注意力分数。在机器学习中，常见的利用Softmax函数达到归一化的目的。具体的公式表达如下：
$${\alpha }_{ij}=soft\underset{j}{\max }\left(e_{ij}\right)=\frac{\exp \left(e_{ij}\right)}{{\sum }_{k\in N_i}\exp \left(e_{ik}\right)}$$
式中，$N_i$表示节点$i$所有的邻接节点。
该式的输出就是我们想要的注意力分数，但是该注意力分数是不稳定的。因此我们需要考虑多层注意力。

4、多层注意力

多层注意力是指组合多个嵌入向量的注意力分数代替单个注意力分数。为实现这一步，我们仅需重复前三个步骤即可。每个节点产生一个嵌入向量$h_i^k$，$k$在此处代表索引。之后，有两种方法将多个嵌入向量相结合。

• 计算平均：第一种方法是对多个嵌入向量求平均：
  $$h_i=\frac{1}{n}\sum _{k=1}^n{h}_i^k=\frac{1}{n}\sum _{k=1}^n\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{\mathbf{w}}^k{x}_j$$
• 首尾连接：第二种方法是将不同的嵌入向量相连接，产生一个较大的矩阵：
  h i = ∥ k = 1 n h i k = ∥ k = 1 n ∑ j ∈ N i α i j k W k x j h_i=\left\| _{k=1}^{n}h_{i}^{k}= \right\| _{k=1}^{n}\sum_{j\in \mathcal{N} _i}{\alpha _{ij}^{k}}\mathbf{W}^kx_j hi​= ​k=1n​hik​= ​k=1n​j∈Ni​∑​αijk​Wkxj​
  当实践中，我们可以在隐藏层选择首尾连接的方法处理嵌入向量，在最后一层使用计算平均的方法处理嵌入向量。
  综上，网络流程图如图2所示。
  

图2 用多层注意力计算注意力分数

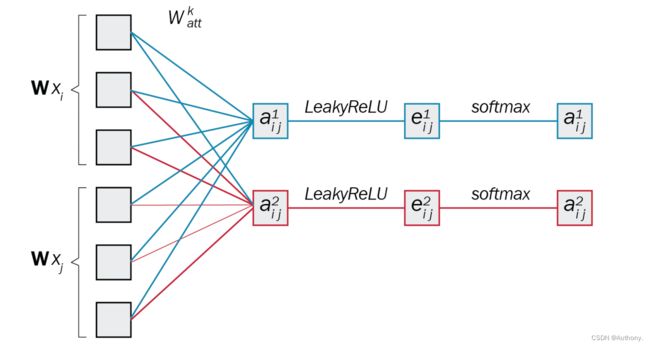
5、改进注意力层

在上述注意力分数的计算过程中，我们的注意力层只能计算静态的数据，为此，提出了GATv2，该模型可以用来计算动态的数据。
GATv2改变了计算的顺序，两者的比较如下：
GATs
$${\alpha }_{ij}=\frac{\exp \left(Leaky\mathrm{Re}LU\left(W_{att}^T\left[W{x}_i\Vert W{x}_j\right]\right)\right)}{{\sum }_{k\in N_i}\exp \left(Leaky\mathrm{Re}LU\left(W_{att}^T\left[W{x}_i\Vert W{x}_k\right]\right)\right)}$$
GATv2
$${\alpha }_{ij}=\frac{\exp \left(W_{att}^{T}Leaky\mathrm{Re}LU\left(\left[W{x}_i\Vert W{x}_j\right]\right)\right)}{{\sum }_{k\in N_i}\exp \left(W_{att}^{T}Leaky\mathrm{Re}LU\left(\left[W{x}_i\Vert W{x}_k\right]\right)\right)}$$

二、Cora分类数据集

介绍完原理后，我们将GATs应用于实例中。

1、导入数据库

import torch
import numpy as np
import torch.nn.functional as F
import matplotlib.pyplot as plt
from torch_geometric.utils import degree
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import GATv2Conv, GCNConv
from torch.nn import Linear, Dropout

np.random.seed(42)
torch.manual_seed(42)
torch.cuda.manual_seed(42)
torch.cuda.manual_seed_all(42)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False

2、GATs类

建立GATs类函数。

# Import dataset from PyTorch Geometric
dataset = Planetoid(root=".", name="Cora")
data = dataset[0]

def accuracy(y_pred, y_true):
    """Calculate accuracy."""
    return torch.sum(y_pred == y_true) / len(y_true)


class GAT(torch.nn.Module):
    def __init__(self, dim_in, dim_h, dim_out, heads=8):
        super().__init__()
        self.gat1 = GATv2Conv(dim_in, dim_h, heads=heads)
        self.gat2 = GATv2Conv(dim_h*heads, dim_out, heads=1)

    def forward(self, x, edge_index):
        h = F.dropout(x, p=0.6, training=self.training)
        h = self.gat1(h, edge_index)
        h = F.elu(h)
        h = F.dropout(h, p=0.6, training=self.training)
        h = self.gat2(h, edge_index)
        return F.log_softmax(h, dim=1)

    def fit(self, data, epochs):
        criterion = torch.nn.CrossEntropyLoss()
        optimizer = torch.optim.Adam(self.parameters(), lr=0.01, weight_decay=0.01)

        self.train()

        losses = []
        accs = []
        val_losses = []
        val_accs = []

        for epoch in range(epochs+1):
            optimizer.zero_grad()
            out = self(data.x, data.edge_index)
            loss = criterion(out[data.train_mask], data.y[data.train_mask])
            acc = accuracy(out[data.train_mask].argmax(dim=1), data.y[data.train_mask])
            loss.backward()
            optimizer.step()

            val_loss = criterion(out[data.val_mask], data.y[data.val_mask])
            val_acc = accuracy(out[data.val_mask].argmax(dim=1), data.y[data.val_mask])
            print(f'Epoch {epoch:>3} | Train Loss: {loss:.3f} | Train Acc: {acc*100:>5.2f}% | Val Loss: {val_loss:.2f} | Val Acc: {val_acc*100:.2f}%')

            loss = loss.detach().numpy()
            acc = acc.detach().numpy()
            val_loss = val_loss.detach().numpy()
            val_acc = val_acc.detach().numpy()

            losses.append(loss)
            accs.append(acc)
            val_losses.append(val_loss)
            val_accs.append(val_acc)

        self.train_loss = losses
        self.train_acc = accs
        self.val_loss = val_losses
        self.val_acc = val_accs

    @torch.no_grad()
    def test(self, data):
        self.eval()
        out = self(data.x, data.edge_index)
        acc = accuracy(out.argmax(dim=1)[data.test_mask], data.y[data.test_mask])
        return acc

在上述代码中，需要注意$GATv2Conv$函数中的$heads$超参数代表了多层注意力所用的嵌入向量个数，另一个超参数$concat=False$代表了使用计算平均的方法而非首尾相连。

3、训练GATv2模型

# Create the Vanilla GNN model
gat = GAT(dataset.num_features, 32, dataset.num_classes)
print(gat)

# Train
gat.fit(data, epochs=100)

# Test
acc = gat.test(data)
print(f'GAT test accuracy: {acc*100:.2f}%')

# plot
num = range(1, len(gat.train_loss)+1)

plt.plot(num, gat.train_loss, label="Training loss")
plt.plot(num, gat.val_loss, ":", label="Val loss")
plt.title("GATv2 Training and validation loss")
plt.style.use('seaborn-colorblind')
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.show()

plt.plot(num, gat.train_acc, label="Training acc")
plt.plot(num, gat.val_acc, ':', label="Val acc")
plt.style.use('seaborn-colorblind')
plt.title("GATv2 Training and validation acc")
plt.xlabel("Epochs")
plt.ylabel("acc")
plt.legend()
plt.show()

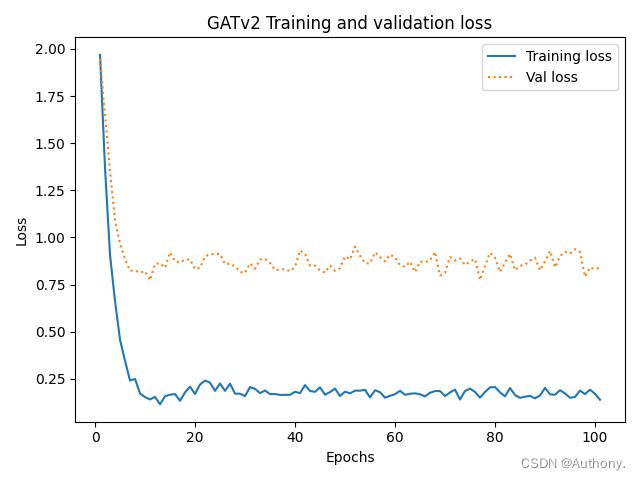
经过模型训练，可以得到训练结果如图3所示。

图3 GATv2训练集和验证集的loss和val曲线

从图3中可以看出，模型并没有过拟合，可以作为预测模型。预测得到测试集的准确率为82.3%，相较于GCNs有所提升。

# Get model's classifications
out = gat(data.x, data.edge_index)

# Calculate the degree of each node
degrees = degree(data.edge_index[0]).numpy()

# Store accuracy scores and sample sizes
accuracies = []
sizes = []

# Accuracy for degrees between 0 and 5
for i in range(0, 6):
    mask = np.where(degrees == i)[0]
    accuracies.append(accuracy(out.argmax(dim=1)[mask], data.y[mask]))
    sizes.append(len(mask))

# Accuracy for degrees > 5
mask = np.where(degrees > 5)[0]
accuracies.append(accuracy(out.argmax(dim=1)[mask], data.y[mask]))
sizes.append(len(mask))

# Bar plot
fig, ax = plt.subplots()
ax.set_xlabel('Node degree')
ax.set_ylabel('Accuracy score')
plt.bar(['0','1','2','3','4','5','6+'], accuracies)
for i in range(0, 7):
    plt.text(i, accuracies[i], f'{accuracies[i]*100:.2f}%', ha='center', color='black')
for i in range(0, 7):
    plt.text(i, accuracies[i]//2, sizes[i], ha='center', color='white')

plt.show()

另外通过上述代码我们可以得到图4。

图4 不同邻接节点个数的准确率 从图4中可以看出，邻接节点较少的节点其模型的预测准确率要低于邻接节点较多的节点。这是正常的，因为较多的邻接节点会给模型预测提供更多的信息。

---

总结

在本章中，我们介绍了一个新的基本架构:GAT。从线性变换到多层注意力，我们通过四个主要步骤来了解其内部工作原理。我们通过在NumPy中实现一个图形注意层来了解它是如何在实践中工作的。最后，我们将GAT模型（带有GATv2）应用于Cora数据集，在那里它提供了出色的准确性分数。我们证明了这些分数依赖于邻居的数量。