GraphSAGE

GraphSAGE是GNN架构下专门设计的结构用于应对大数据集。对于科技公司而言，模型的可伸缩性对于模型后续的改进至关重要。因此，催生了GraphSAGE架构，其相较于GCNs和GATs有根本性的不同。

---

前言

在本文中，我们将学习GraphSAGE的中心思想。首先，我们将描述其采样邻接节点的方法，这是GraphSAGE架构的核心。其次，我们将探索三种不同的方法去生成嵌入向量。

另外，GraphSAGE在模型训练上提出了新的可能性，我们将利用此架构训练两个任务。其一是PubMed数据集的节点分类问题，其二是protein-protein interactions数据集的多标签分类问题。最后，我们将讨论归纳法的优点。

---

一、GraphSAGE原理

GraphSAGE可以归纳大型数据集，它用于产生嵌入向量并将其用于下流任务。另外，它解决了GCNs和GATs在大型数据集上效果较差以及无法有效预测不可见数据集的问题。

首先，我们介绍GraphSAGE架构的两个要素：

• 采样邻接节点
• 聚合向量

1、采样邻接节点

在神经网络的训练中，经常将数据集分为相同大小的不同批次（batches）。这些不同的批次将被用于梯度下降，在训练过程中不断优化算法以寻找最优的权重以及偏置值。梯度下降的方法大抵上有三种：

• 批量梯度下降（Batch gradient descent）：权重和偏置的更新在训练完训练集的数据之后（epoch），这种方法的训练速度较慢，并且需要一定的内存空间。
• 随机梯度下降（Stochastic gradient descent）：权重和偏置的更新在每一个训练样本之后，这种方法会增大噪声值的引入，因为误差是不平均的。但是，它适用于在线实时训练的情况。
• Mini-batch梯度下降：权重和偏置的更新在每一批次训练结束后，这种方法的速度较快，因为不同的批次可以被GPU平行处理，并且它的收敛更加稳定。

在实践中，我们可以使用高级优化器，例如RMSprop或者Adam，它们可以实现批次的处理。

那么，我们应该如何划分表格数据集，使节点的整体结构不会被破坏呢？
在GNN架构中，每一个邻接节点都被用于计算节点的嵌入向量，这意味着每计算一层嵌入向量，需要目标节点的邻接节点参与（1 hop）。如果我们用于两层GNN架构，我们就需要目标节点的邻接节点，以及邻接节点的邻接节点（2 hops）。通过图1，我们可以观察到上述关系。

图1 目标节点0的邻接节点图

这种方法可以应用于填充批次中，图2描述了计算节点嵌入的序列操作。

图2 节点0的嵌入流程

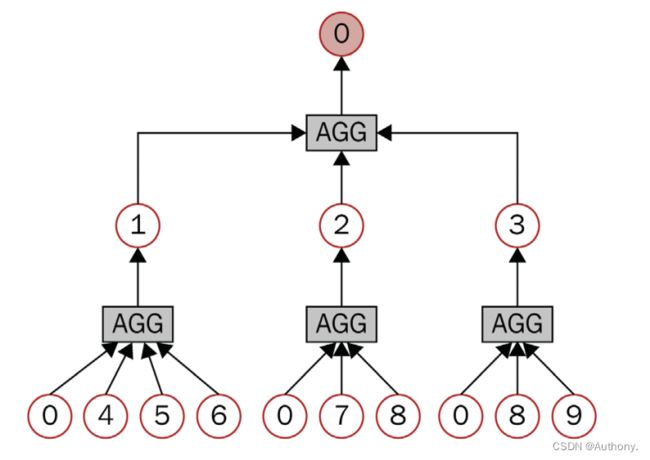
通过聚合2-hop的邻接节点可以嵌入得到1-hop处邻接节点，这些嵌入值再次通过聚合可以得到中心节点的嵌入向量。然而，上述设计有两个问题：

• 计算邻接节点的嵌入向量的时间将呈现指数级的增长。
• 具有大量邻接节点的节点，也叫做枢纽节点（hub nodes）将会产生庞大的计算图。

为了解决上述问题，我们将限制计算图的大小。例如，我们将在1-hop处保留3个邻接节点，在2-hop处保留5个邻接节点，进而我们只需要计算15个节点向量即可。
采集较少的邻接节点会使时间复杂度降低，但是会导致训练更加随机，产生比较大的方差。此外，GNN的层数必须较少，以避免指数级增大的计算图。邻接节点会修剪重要的信息来进行权衡，这可能会使得精度下降。
我们可以采用PinSAGE的方法，其保留了固定数量的邻接节点，但是在节点的筛选上使用了随机游走的抽样方法，借此选择出现频率较高的节点。这种方法可以确定邻接节点之间的相对重要性。

2、聚合向量

在选择完邻接节点后，我们需要聚合嵌入向量，在GraphSAGE中，主要有三种方法：

• 平均值聚合
• LSTM聚合
• 池化层聚合

我们将着重关注平均值聚合，其实现难度较低。该方法主要是将目标节点和邻接节点的嵌入向量相结合求平均，之后加入权重矩阵进行线性变换，加入激活函数实现非线性变换。
其公式表达如下：
$$h_i^{\prime }=\sigma \left(\mathbf{W}\cdot {\mathrm{mean}}_{j\in {\tilde{\mathcal{N}}}_i}\left(h_j\right)\right)$$
在GraphSAGE中，我们将目标节点单独提出，公式变更为：
$$h_i^{\prime }=\sigma \left({\mathbf{W}}_1{h}_i+{\mathbf{W}}_2\cdot {\mathrm{mean}}_{j\in {\mathcal{N}}_i}\left(h_j\right)\right)$$
LSTM聚合器基于LSTM架构，这是一种流行的递归神经网络类型。与均值聚合器相比，LSTM聚合器理论上可以区分更多的图结构，从而产生更好的嵌入。问题在于，LSTM只考虑输入序列，比如一个有开头和结尾的句子。但是，节点没有任何顺序。因此，我们对节点的邻居进行随机排列来解决这个问题。该解决方案允许我们使用LSTM体系结构，而不依赖于任何输入序列。

最后，池聚合器分两步工作。首先，将每个邻接节点的嵌入向量送入MLP以产生一个新的向量。其次，执行元素最大化操作，只保留每个特征的最大值。

二、PubMed数据集分类

PubMed数据集具有19717个节点以及88648个边，是一个较为庞大的数据集。其可视化图如图3所示。

图3 PubMed可视化图 其节点特征向量由TF-ADF加权词向量得到，我们的目标是判断节点属于三类中的哪一类。

1、导入数据库

import torch
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
import torch.nn.functional as F
import time

from torch_geometric.nn import SAGEConv
from torch_geometric.datasets import Planetoid
from torch_geometric.loader import NeighborLoader
from torch_geometric.utils import to_networkx

torch.manual_seed(42)
torch.cuda.manual_seed(42)
torch.cuda.manual_seed_all(42)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False

2、采样邻接节点

dataset = Planetoid(root='.', name="Pubmed")
data = dataset[0]

start_time = time.time()
# Create batches with neighbor sampling
# data.train_mask=range(0, 60) --> range(0, 16), range(16, 32) ... range(48, 60)
train_loader = NeighborLoader(
                        data,
                        num_neighbors=[5, 10],
                        batch_size=16,
                        input_nodes=data.train_mask, # the indices of nodes for which neighbors are sampled
                        )

# sampled_data = next(iter(train_loader))
# print(sampled_data.n_id)

# Print each subgraph
# shape of x
for i, subgraph in enumerate(train_loader):
    print(f'Subgraph {i}: {subgraph}')

# Plot each subgraph
fig = plt.figure(figsize=(16,16))
for idx, (subdata, pos) in enumerate(zip(train_loader, [221, 222, 223, 224])):
    G = to_networkx(subdata, to_undirected=True)
    ax = fig.add_subplot(pos)
    ax.set_title(f'Subgraph {idx}', fontsize=24)
    plt.axis('off')
    nx.draw_networkx(G,
                    pos=nx.spring_layout(G, seed=0),
                    with_labels=False,
                    node_color=subdata.y,
                    )
plt.show()

在上述代码中，我们将1-hop设置为5个节点，2-hop设置为10个节点，并将单个批次的中心节点数量设置为16个，并通过$input\_nodes$设置中心节点的选择范围。

运行代码后可以得到图4。

图4 采样邻接节点得到的子图 从图4中可以发现，中心节点的邻接节点在类型上具有一致性。

3、GraphSAGE类

定义类函数如下。

def accuracy(pred_y, y):
    """Calculate accuracy."""
    return ((pred_y == y).sum() / len(y)).item()


class GraphSAGE(torch.nn.Module):
    """GraphSAGE"""
    def __init__(self, dim_in, dim_h, dim_out):
        super().__init__()
        self.sage1 = SAGEConv(dim_in, dim_h)
        self.sage2 = SAGEConv(dim_h, dim_out)

    # graphsage forward
    def forward(self, x, edge_index):
        # transductive learning can only generate embeddings for a fixed graph
        # doesn't generalize for unseen nodes or graphs
        # but GraphSAGE is considered an inductive framework
        h = self.sage1(x, edge_index)
        h = torch.relu(h)
        h = F.dropout(h, p=0.5, training=self.training)
        h = self.sage2(h, edge_index)
        return h

    def fit(self, loader, epochs):
        criterion = torch.nn.CrossEntropyLoss()
        optimizer = torch.optim.Adam(self.parameters(), lr=0.01)

        self.train()
        for epoch in range(epochs+1):
            total_loss = 0
            acc = 0
            val_loss = 0
            val_acc = 0

            # Train on batches
            for batch in loader:
                optimizer.zero_grad()
                # forward
                out = self(batch.x, batch.edge_index)
                loss = criterion(out[batch.train_mask], batch.y[batch.train_mask])
                total_loss += loss.item()
                acc += accuracy(out[batch.train_mask].argmax(dim=1), batch.y[batch.train_mask])
                loss.backward()
                optimizer.step()

                # Validation
                val_loss += criterion(out[batch.val_mask], batch.y[batch.val_mask])
                val_acc += accuracy(out[batch.val_mask].argmax(dim=1), batch.y[batch.val_mask])

            # Print metrics every 10 epochs
            if epoch % 20 == 0:
                print(f'Epoch {epoch:>3} | Train Loss: {loss/len(loader):.3f} | Train Acc: {acc/len(loader)*100:>6.2f}% | Val Loss: {val_loss/len(train_loader):.2f} | Val Acc: {val_acc/len(train_loader)*100:.2f}%')

    @torch.no_grad()
    def test(self, data):
        self.eval()
        out = self(data.x, data.edge_index)
        acc = accuracy(out.argmax(dim=1)[data.test_mask], data.y[data.test_mask])
        return acc

在上述代码中，构建了两层GraphSAGE架构，$SAGEConv$函数在为指定$aggr$超参数的情况下，默认采用平均值聚合。$root\_weight$超参数在默认的情况下为$True$，即图层会向输出添加转换后的根节点特征。

下面的代码表述了$SAGEConv$函数的计算过程，其中$propagate$函数计算邻接节点的采样结果得到相对应的嵌入向量，嵌入向量经过$lin\_l$（带偏置的线性函数中）函数得到输出结果，在默认的$root\_weight$超参数下，输出结果还会加上根节点的特征。

# propagate_type: (x: OptPairTensor)
out = self.propagate(edge_index, x=x, size=size)
out = self.lin_l(out)

x_r = x[1]
# the layer will add transformed root node features to the output
if self.root_weight and x_r is not None:
    out = out + self.lin_r(x_r)

3、训练GraphSAGE模型

# Create GraphSAGE
graphsage = GraphSAGE(dataset.num_features, 64, dataset.num_classes)
print(graphsage)

# Train
graphsage.fit(train_loader, 200)

# Test
acc = graphsage.test(data)
print(f'GraphSAGE test accuracy: {acc*100:.2f}%')

end_time = time.time()
print('time cost:', (end_time-start_time))

得到测试集的预测准确率为75%。
相较于GCNs和GATs架构来说，GraphSAGE的训练速度很快，并且可以处理更大的图。

三、归纳法学习PPI数据集

在GNN中，我们将区分两种类型的学习-直推式学习（transductive）和归纳式学习（inductive）。它们的区别如下：

• 归纳式学习中，GNN在训练过程中只看到训练集的数据，训练集的标签被用来调整GNN参数。即从已有数据中归纳出模型应用于新数据。
• 直推式学习中，GNN在训练过程中看到来自训练集和测试集的数据，然后从训练集中学习数据，并将标签用于信息扩散。即给一部分测试数据，观察能否结合已有数据推广到测试数据中。

直推式学习学习只能生成固定图的嵌入；它不能泛化不可见的节点或图。然而，由于邻接节点抽样，GraphSAGE被设计成在局部级别使用修剪的计算图进行预测。它被认为是一个归纳式学习，因为它可以应用于具有相同特征模式的任何计算图。

1、库函数导入

import torch
import time
from sklearn.metrics import f1_score

from torch_geometric.datasets import PPI
from torch_geometric.data import Batch
from torch_geometric.loader import DataLoader, NeighborLoader
from torch_geometric.nn import GraphSAGE

torch.manual_seed(42)
torch.cuda.manual_seed(42)
torch.cuda.manual_seed_all(42)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False

2、数据集导入和划分

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

time_start = time.time()

# Load training, evaluation, and test sets
# multi-label classification with 121 labels
train_dataset = PPI(root=".", split='train')
val_dataset = PPI(root=".", split='val')
test_dataset = PPI(root=".", split='test')

for content in train_dataset:
    print(content)

train_data = Batch.from_data_list(train_dataset)
print(train_data)

# Unify the training graphs in a single set and apply neighbor sampling
train_loader = NeighborLoader(train_data,
                              batch_size=2048,
                              shuffle=True,
                              num_neighbors=[20, 10],
                              num_workers=2,             # you have at most 2 workers simultaneously putting data into RAM
                              persistent_workers=True)  # If True, the data loader will not shutdown the worker processes after a dataset has been consumed once.

# Evaluation loaders (one datapoint corresponds to a graph)
# create batches 
val_loader = DataLoader(val_dataset, batch_size=2)
test_loader = DataLoader(test_dataset, batch_size=2)

在上述代码中，数据集已经被划分为不同批次的图，其中训练集有20个批次，测试集和验证集有2个批次。我们将训练集的批次通过$from\_data\_list$整合，并重新用$NeighborLoader$函数生成不同批次的数据。

3、模型建立

model = GraphSAGE(
    in_channels=train_dataset.num_features,
    hidden_channels=512,
    num_layers=2,
    out_channels=train_dataset.num_classes,
).to(device)

criterion = torch.nn.BCEWithLogitsLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)

def fit(loader):
    model.train()

    total_loss = 0
    for data in loader:
        data = data.to(device)
        optimizer.zero_grad()
        out = model(data.x, data.edge_index)
        loss = criterion(out, data.y)
        total_loss += loss.item() * data.num_graphs
        loss.backward()
        optimizer.step()
    return total_loss / len(loader.data)

@torch.no_grad()
def test(loader):
    model.eval()

    data = next(iter(loader))
    out = model(data.x.to(device), data.edge_index.to(device))
    preds = (out > 0).float().cpu()

    y, pred = data.y.numpy(), preds.numpy()
    return f1_score(y, pred, average='micro') if pred.sum() > 0 else 0

data_loader = next(iter(val_loader))
print(data_loader)
print(train_dataset.num_classes)

由于$num\_layers$的数值为2，因此模型可以同时处理两个批次的数据，所以不需要在另外划分验证集和测试集。

4、模型训练

for epoch in range(201):
    loss = fit(train_loader)
    val_f1 = test(val_loader)
    if epoch % 20 == 0:
        print(f'Epoch {epoch:>3} | Train Loss: {loss:.3f} | Val F1-score: {val_f1:.4f}')

print(f'Test F1-score: {test(test_loader):.4f}')

time_end = time.time()
print(time_end-time_start)

输出结果如下。

Epoch   0 | Train Loss: 12.712 | Val F1-score: 0.4858
Epoch  20 | Train Loss: 9.032 | Val F1-score: 0.7673
Epoch  40 | Train Loss: 8.805 | Val F1-score: 0.7885
Epoch  60 | Train Loss: 8.692 | Val F1-score: 0.8024
Epoch  80 | Train Loss: 8.637 | Val F1-score: 0.8068
Epoch 100 | Train Loss: 8.591 | Val F1-score: 0.8128
Epoch 120 | Train Loss: 8.570 | Val F1-score: 0.8152
Epoch 140 | Train Loss: 8.543 | Val F1-score: 0.8166
Epoch 160 | Train Loss: 8.524 | Val F1-score: 0.8188
Epoch 180 | Train Loss: 8.517 | Val F1-score: 0.8226
Epoch 200 | Train Loss: 8.501 | Val F1-score: 0.8217
Epoch 220 | Train Loss: 8.474 | Val F1-score: 0.8253
Epoch 240 | Train Loss: 8.472 | Val F1-score: 0.8260
Epoch 260 | Train Loss: 8.470 | Val F1-score: 0.8239
Epoch 280 | Train Loss: 8.463 | Val F1-score: 0.8258
Epoch 300 | Train Loss: 8.439 | Val F1-score: 0.8265
Test F1-score: 0.8505
1923.0157027244568

通过得到的结果，我们可以认为模型具有归纳式学习，因为测试集的数据处于不同的图例和加载器中。

---

总结

本文介绍了GraphSAGE框架及其两个组成部分——邻接节点采样算法和三个聚合算子。邻接节点采样是GraphSAGE在短时间内处理大型图的核心。它还负责归纳设置，这允许它将预测推广到看不见的节点和图。我们在PubMed上测试了一种转换情况，并在PPI数据集上测试了一种感应情况，以执行一种新的任务-多标签分类。虽然不如GCN或GAT准确，但GraphSAGE是处理大量数据的流行且高效的框架。