万能Markdown数学公式

万能Markdown数学公式

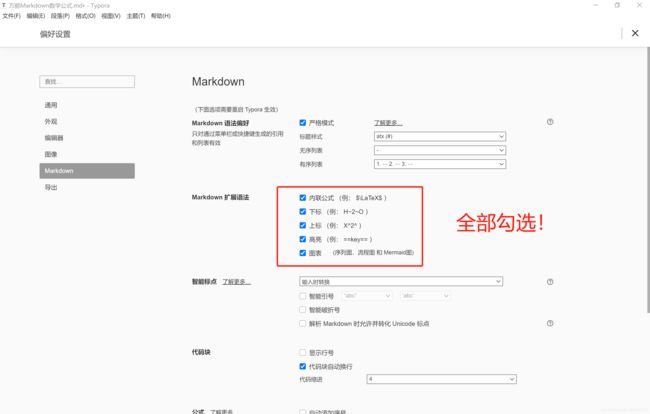
1、首先设置（windows）：

• 文件 —> 偏好设置 —> Markdown —> 勾选Markdown扩展语法

• 设置完成，Mac系统，也找到对应的设置，进行设置

2、markdown格式

在markdown中展示数学公式，使用一对$$，或者四个$$$$

效果如下：

• ${\frac{-b \pm \sqrt{b^2-4ac}}{2a}}$ —> $\frac{-b\pm \sqrt{b^2-4ac}}{2a}$
• $$-b \pm \sqrt{b^2-4ac} \over 2a$$ —> $\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

这数学公式效果是不是非常炫酷啊，下面跟着我一起来学习吧！我主要使用一对$进行公式书写~

3、上下标

^ 表示上标, _ 表示下标。如果上下标的内容多于一个字符，需要用 {} 将这些内容括成一个整体。上下标可以嵌套，也可以同时使用。

上标语法：

$x^{y^z}=(1+e^x)^{-2xy^w}$

• 显示：

  $x^{y^z}=(1+e^x{)}^{-2x{y}^w}$

公式有点小，进行放大，并改变颜色：

$x^{y^z}=(1+e^x)^{-2xy^w}$

• 显示：

  $x^{y^z}=(1+e^x{)}^{-2x{y}^w}$

你仔细观察字母e有点斜，可以使用{\rm e} 来矫正

$x^{y^z}=(1+{\rm e}^x)^{-2xy^w}$

• 显示：

  $x^{y^z}=(1+{\mathrm{e}}^x{)}^{-2x{y}^w}$

先写下标再写上标：

$C_n^2$

• 显示：

  $C_n^2$

4、分式与根号

\frac{}{} 表示分式，第一个花括号内容为分子，第二个花括号内容为分母

示例：

$f(x,y) = \frac{x + y}{3x^2 + 4y^{2.5}}$

显示：

$f(x,y)=\frac{x+y}{3x^2+4y^{2.5}}$

\sqrt{}表示开根号，\sqrt[]{}中括号表示开几次方，后面花括号为开方内容

$f(x,y) = \frac{\sqrt[3]{x^2 + y^3}}{3x^2 +4y^{2.5}}$

显示：

$f(x,y)=\frac{\sqrt[3]{x^2+y^3}}{3x^2+4y^{2.5}}$

5、累加与累乘

使用 \sum 来输入一个累加。与之类似，使用 \prod `来输入累乘。

示例：

$\sum\limits_{i = 1}^nf(x_i)$

显示：

$\sum _{i=1}^{n}f(x_i)$

示例：

$\prod\limits_{i = 1}^n(x_i-1)(x_i + 2)$

显示：

$\prod _{i=1}^n(x_i-1)(x_i+2)$

6、括号

()、[] 和 | 表示符号本身，使用 \{\} 来表示 {} 。当要显示大号的括号时，要用 \left 和 \right 命令

示例：

$f(x,y,z) = 2y^3z \left( 7+\frac{5x+8}{4+y^3} \right)$

显示：

$f(x,y,z)=2y^{3}z\left(7+\frac{5x+8}{4+y^3}\right)$

示例：

$\frac{du}{dx}|_{x = 0}$

显示：

$\frac{du}{dx}{|}_{x=0}$

7、省略号

数学公式中常见的省略号有两种，\ldots 表示与文本底线对齐的省略号，\cdots 表示与文本中线对齐的省略号。

示例：

$f(x_1,x_2,\cdots,x_n) = x_1^2 + x_2^2 + \cdots + x_n^2$

显示：

$f(x_1,x_2,\cdots ,x_n)=x_1^2+x_2^2+\cdots +x_n^2$

示例：

$f(x_1,x_2,\ldots,x_n) = x_1^2 + x_2^2 + \ldots + x_n^2$

显示：

$f(x_1,x_2,\dots ,x_n)=x_1^2+x_2^2+\dots +x_n^2$

8、矢量

使用 \vec{矢量} 来自动产生一个矢量。也可以使用 \overrightarrow 等自定义字母上方的符号。\cdot 表示一个点，在公式中往往表示向量乘法。

示例：

$\vec{a} \cdot \vec{b}$

显示：

$a\cdot b$

左箭头，两边箭头，右箭头示例，其中\quad 表示四个空格：

$\overleftarrow{xy} \quad  \overleftrightarrow{xy} \quad \overrightarrow{xy}$

显示：

$xyxyxy$

9、积分

使用 \int 来输入一个积分。

示例：

$\int_0^1 {x^2} {\rm d}x$

显示：

${\int }_0^1{x}^2\mathrm{d}x$

10、极限运算

使用 \lim 来输入一个极限。\to 表示从箭头 ，\infty 表示无穷大，\limits表示置于正下方。

示例：

$\lim\limits_{n \to +\infty} \frac{1}{n(n+1)}$

显示：

$\underset{n\to +\infty }{\lim }\frac{1}{n(n+1)}$

11、常用希腊字母

常用希腊字母：

小写	markdown	大写	markdown
$\mathrm{A}$	$\Alpha$	$\alpha$	$\alpha$
$\Delta$	$\Delta$	$\delta$	$\delta$
$\Lambda$	$\Lambda$	$\lambda$	$\lambda$
$\mathrm{H}$	$\Eta$	$\eta$	$\eta$
$\mathrm{E}$	$\Epsilon$	$ϵ$	$\epsilon$
$\Theta$	$\Theta$	$\theta$	$\theta$
$\mathrm{B}$	$\Beta$	$\beta$	$\beta$
$\Pi$	$\Pi$	$\pi$	$\pi$
$\Phi$	$\Phi$	$\varphi$	$\phi$
$\Psi$	$\Psi$	$\psi$	$\psi$
$\Omega$	$\Omega$	$\omega$	$\omega$
$\nabla$	$nabla$	……	……

更多希腊字母，参考百度百科：

希腊字母

12、方程组

表达式一：需要cases环境，起始、结束处以{cases}声明

$\begin{cases}
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3\\
\end{cases}$

显示：
$\{\begin{array}{l}{a}_{1}x+b_{1}y+c_{1}z=d_1\\ a_{2}x+b_{2}y+c_{2}z=d_2\\ a_{3}x+b_{3}y+c_{3}z=d_3\end{array}$

表达方式二: 使用\begin{array}\\ 表达式一\\表达式二... \end{array}

$\left\{\begin{array} \\
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3\\
\end{array}\right.$

显示：（左边\left表示显示大的花括号，右边\right.表示不显示右边，\left和\right必须成对出现~）

$$\begin{gathered} \{\begin{array}{c} \\ {a}_{1}x+b_{1}y+c_{1}z=d_1\\ a_{2}x+b_{2}y+c_{2}z=d_2\\ a_{3}x+b_{3}y+c_{3}z=d_3\end{array} \end{gathered}$$

表达式三：需要align环境，起始、结束处以{align}声明，align表示对齐（也可以使用aligned，公式中的&表示对齐）

$f(x,y,z) = \left \{\begin{aligned} &3x + 5y +  z \quad &, x < 0  \\ &7x - 2y + 4z\quad&, x > 0 \\ &-6x + 3y + 2z \quad &,x = 0\end{aligned}\right.$

显示：

$f(x,y,z)=\{\begin{array}{rlr}& 3x+5y+z& ,x<0\\ & 7x-2y+4z& ,x>0\\ & -6x+3y+2z& ,x=0\end{array}$

复杂公式推导示例：（四个\\\\表示两次换行）

$\begin{aligned}l(\theta) &= \sum\limits_{i = 1}^n\log p(y^{(i)}|x^{(i)};\theta) \\ \\&=\sum\limits_{i = 1}^n\log\prod\limits_{j = 1}^k\phi_j^{I\{{y^{(i)} = j\}}}\\\\&= \sum\limits_{i = 1}^n\log\prod\limits_{j = 1}^k(\frac{e^{\theta_j^Tx^{(i)}}}{\sum\limits_{l = 1}^ke^{\theta_l^Tx^{(i)}}})^{I\{{y^{(i)} = j\}}}\end{aligned}$

显示：

$\begin{array}{rl}l(\theta )& =\sum _{i=1}^n\log p(y^{(i)}|x^{(i)};\theta )\\ & \\ & =\sum _{i=1}^n\log \prod _{j=1}^k{\varphi }_j^{I\{y^{(i)}=j\}}\\ & \\ & =\sum _{i=1}^n\log \prod _{j=1}^k(\frac{e^{{\theta }_j^T{x}^{(i)}}}{\sum _{l=1}^k{e}^{{\theta }_l^T{x}^{(i)}}}{)}^{I\{y^{(i)}=j\}}\end{array}$

13、矩阵

使用 \begin{matrix} ... \end{matrix} 生成，每一行以 \\ 结尾表示换行，各元素间以 & 隔开，右边的序号用 \tag{n} 表示。

$\begin{matrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9 \end{matrix}\tag{1}$

显示：
$$\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\text{\hspace{1em}(1)}$$

带大括号

$\left\{\begin{matrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9 \end{matrix}\right\}\tag{2}$

或者：

$$\begin{Bmatrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{Bmatrix}\tag{2}$$

显示：

$$\left\{\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right\}\text{\hspace{1em}(2)}$$

带中括号

$\left[\begin{matrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{matrix}\right]\tag{3}$

或者：

$\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{bmatrix}\tag{3}$

显示：

$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]\text{\hspace{1em}(3)}$$

包含省略号，矩阵：（行省略号\cdots，列省略号\vdots，斜向省略号（左上至右下）\ddots）

$ \left\{ \begin{matrix}1 & 2 & \cdots & 5 \\ 6 & 7 & \cdots & 10 \\ \vdots & \vdots & \ddots & \vdots \\ \alpha & \alpha+1 & \cdots & \alpha+4\end{matrix} \right\}\tag{4} $

显示：

$$\left\{\begin{array}{cccc}1& 2& \cdots & 5\\ 6& 7& \cdots & 10\\ ⋮& ⋮& \ddots & ⋮\\ \alpha & \alpha +1& \cdots & \alpha +4\end{array}\right\}\text{\hspace{1em}(4)}$$

14、常用符号

名称	markdown	预览
乘法	\times	$\times$
除法	\div	$÷$
正负号	\pm	$\pm$
大于	直接写	$>$
小于	直接写	$<$
大于等于	\ge	$\ge$
小于等于	\le	$\le$
正无穷	\infty	$\infty$
负无穷	-\infty	$-\infty$
带帽符号	\hat{y}	$\hat{y}$
不等于	\not=	$\ne$
不等于	\neq	$\ne$
约等于	\approx	$\approx$
因为	\because	$\because$
所以	\therefore	$\therefore$
小空格	\反斜杠后面紧跟空格	$a\ b$呈现为：$ab$
大空格（四个）	\quad	a\quad b呈现为：$ab$
……	……	……