matlab绘图（1）

4.1二维曲线

plot函数
（1）基本用法：plot（x,y)
其中，x，y为坐标。

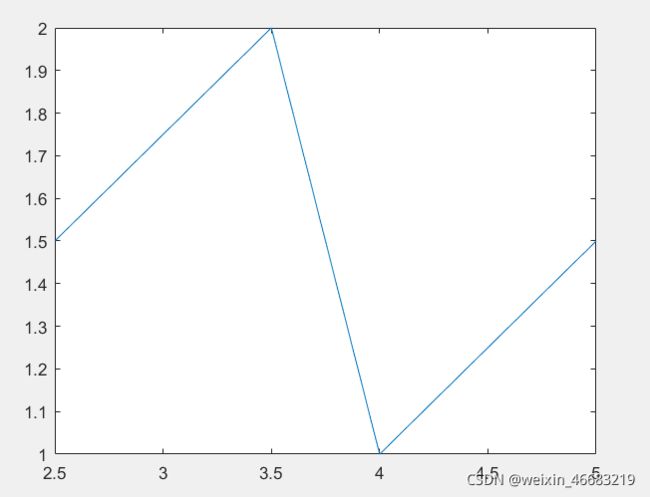
x=[2.5,3.5,4,5];
y=[1.5,2.0,1,1.5];
plot(x,y)

（2）plot最简单的调用格式
plot（x）

x=[1.5,2,1,1.5];
plot(x)

当plot函数的参数x是复数向量时，则分别以该向量元素实部和虚部为横、纵坐标绘制出一条曲线。

x=[2.5,3.5,4,5];
y=[1.5,2.0,1,1.5];

cx=x+y*i; #复向量==（等价于cx=complex（x,y))==
plot(cx)

（3）plot（x,y)函数参数的变化形式

当x是向量，y是矩阵时

• 如果矩阵y的列数等于x的长度，则以向量x为横坐标，以y的每个行向量为纵坐标绘制曲线，曲线的条数等于x的行数。
• 如果矩阵y的行数等于x的长度，则以向量x为横坐标，以y的每个列向量为纵坐标绘制曲线，曲线的条数等于y的列数。

eg：绘制sinx、sin(2x)、sin(0.5x)的函数曲线。

x=linspace(0,2pi,100); #产生0到2pi之间的行向量，100个元素
y=[sin(x);sin(2x);sin(0.5*x)];
plot(x,y)

当x、y是同型矩阵时
以x，y对应列元素为横，纵坐标分别绘制曲线，曲线条数等于矩阵的列数。
如上例：

t=0:0.01:2pi;
t1=t’;
x=[t1,t1,t1]; #这里的x是个矩阵
y=[sin(t1),sin(2t1),sin(0.5*t1)];
plot(x,y)

（4）含多个输入参数的plot函数
plot（x1,y1,x2,y2,……,xn,yn)
其中，每一向量对构成一组数据点的横纵坐标，绘制一条曲线。
eg：采用不同个数的数据点绘制正弦函数曲线，观察曲线形态。

t1=linspace(0,2pi,10);
t2=linspace(0,2pi,20);
t3=linspace(0,2*pi,100);
plot(t1,sin(t1),t2,sin(t2)+1,t3,sin(t3)+2)

（5）含选项的plot函数
plot（x,y,选项）

线形：

• '-'实线
• ':'虚线
• '-.'点画线
• '–'双画线

颜色：

• 'r’red
• 'g’green
• 'b’blue
• 'w’white
• 'k’黑色
• ……

数据点标记：

• ’*‘星号
• ’o‘圆圈
• ’s‘方块
• ’p‘五角星
• ’^‘朝上三角符号

eg：用不同线形和颜色在同一座标内绘制曲线y=2e^-0.5xsin(2pix)及其包络线。

x=[0:pi/50:2pi]’;
y1=2exp(-0.5x)[-1,1]; #包络线
y2=2exp(-0.5x).sin(2pix);
x1=0:0.5:6;
y3=2exp(-0.5x1).sin(2pix1); 乘0等于0
plot(x,y1,‘k-’,x,y2,‘g–’,x1,y3,‘r*’)

fplot函数

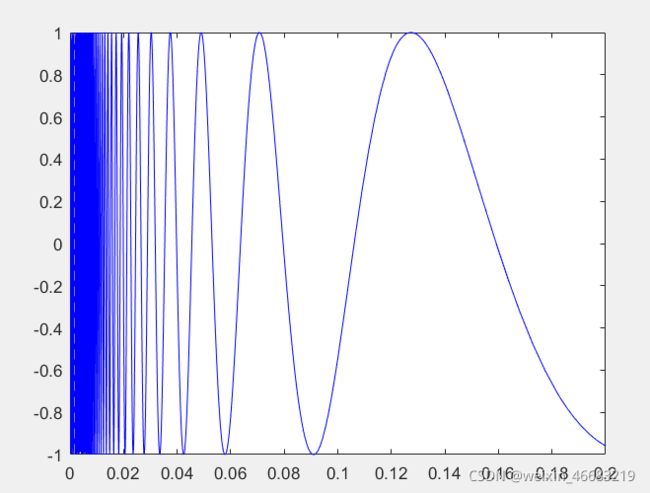
eg：采用fplot绘制sin（1/x)

fplot(@(x) sin(1./x),[0,0.2],‘b’)

如果用plot：

x=[0:0.005:0.2]’;
y=sin(1./x);
plot(x,y)

（2）双输入函数参数的用法
fplot（funx，funy，tlims，选项）

fplot(@(t) t.*sin(t),@(t) t.cos(t),[0,10pi],‘r’)

5.2绘制图形的辅助操作

给图形添加标注

• title
• xlabel（x轴说明）
• ylabel
• text(x,y,图形说明）
• legend（图例1，图例2，……）

（1）title函数
title（图形标题）
eg：绘制[-2pi,2pi]的正弦函数曲线并给图形添加标题

x=-2pi:0.05:2pi;
y=sin(x);
plot(x,y)
title({‘MATLAB’,‘y=sin(x)’})

geq：great than or equal to

（2）xlabel和ylabel函数
xlabel（x轴说明）ylabel（y轴说明）

x=-2pi:0.05:2pi;
y=sin(x);
plot(x,y)
title(‘y=sin(x)’)
xlabel(’-2\pi \leq x \leq 2\pi’)

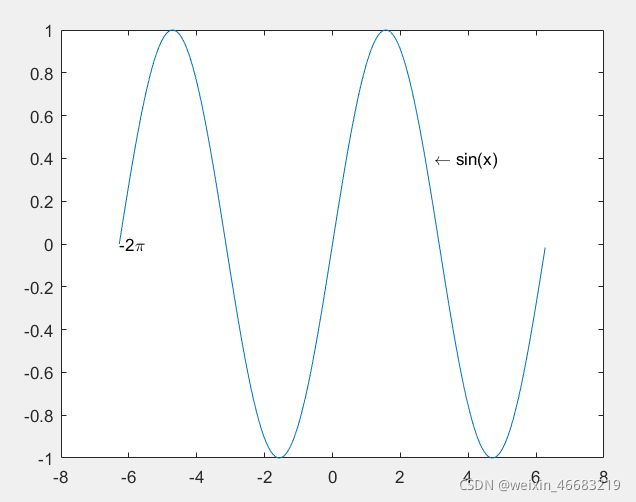
（3）text和gtext函数
text（x，y，说明） gtext（说明）

x=-2pi:0.05:2pi;
y=sin(x);
plot(x,y)
text(-2*pi,0,’-2\pi’)
text(3,0.4,’\leftarrow sin(x)’)

（4）legend函数
legend（图例1，图例2，……）
eg：绘制不同频率的正弦曲线并用图例标注曲线。

x=[0:2pi/100:2pi]’;
y=[sin(x),sin(2x),sin(3x)];
plot(x,y)
legend(‘sin(x)’,‘sin(2x)’,‘sin(3x)’)

坐标控制
（1)axis函数
axis（[xmin,xmax,ymin,ymax,zmin,zmax])
二维图像只用到四个参数

1. axis的其他用法

• axis equal：纵横坐标采用等长刻度
• axis square：产生正方形坐标系
• axis auto：使用默认设置
• axis off：取消坐标轴
• axis on：显示坐标轴

eg：

x=[0,1,1,0,0];
y=[0,0,1,1,0];
plot(x,y)
axis([-0.1,1.1,-0.1,1.1])
axis equal;

（2）给坐标系加网格和边框
网格：

• grid on
• grid off
• grid

边框：（没出现默认有）

• box on
• box off
• box

eg：绘制sinx，sin（2x),sin(x/2)的函数曲线并添加图形标注

x=linspace(0,2pi,100);
y=[sin(x);sin(2x);sin(0.5x)];
plot(x,y)
axis([0,7,-1.2,1.2])
title(‘不同频率的正弦函数曲线’);
xlabel(‘Variable X’);ylabel(‘Variable Y’);
text(2.5,sin(2.5),‘sinx’);
text(1.5,sin(21.5),‘sin(2x)’);
text(5.5,sin(0.5*5.5),‘sin(0.5x)’);
legend(‘sinx’,‘sin(2x)’,‘sin(0.5x)’);
grid on

图形保持
在原有图形上继续画图

1. hold on
2. hold off
3. hold

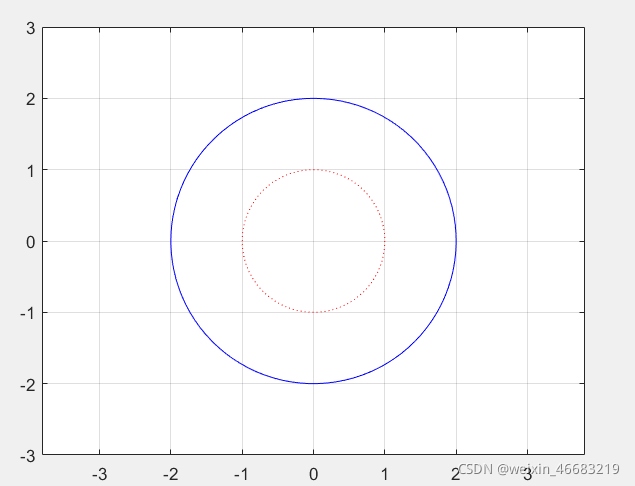
eg:用图形保持功能绘制两个同心圆。

t=linspace(0,2pi,100);
x=sin(t);y=cos(t);
plot(x,y,‘r:’)
hold on;
plot(2x,2*y,‘b’)
grid on;
axis([-3,3,-3,3]);
axis equal

图形窗口的分割

1.子图：同一图形窗口中的不同坐标系下的图形称为子图
2.subplot(m,n,p)
其中，m，n指定将图形窗口分成m*n个绘图区，p指定当前的活动区
eg：

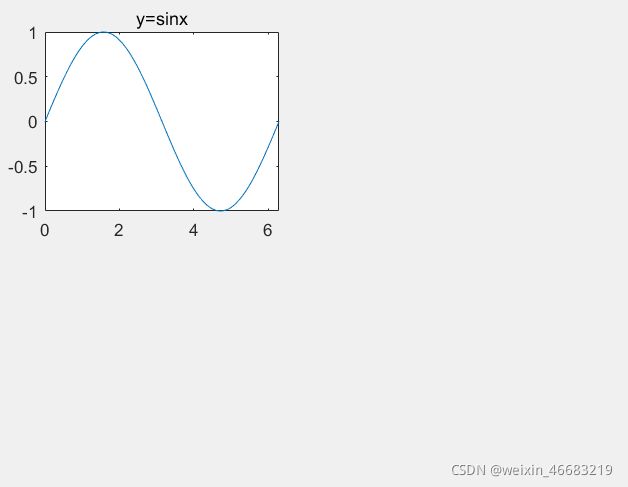
subplot(2,2,1); #分成22个子图，都在第一个图操作
x=linspace(0,2pi,100);
y=sin(x);
plot(x,y)
title(‘y=sinx’);
axis([0,2*pi,-1,1]);

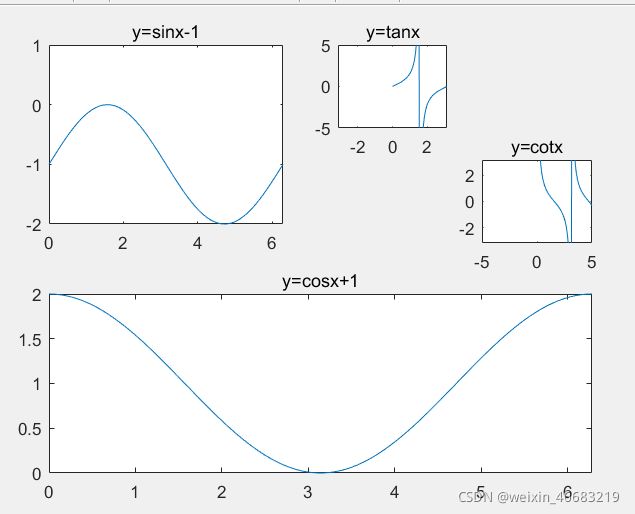
eg：

x=linspace(0,2pi,100);
subplot(2,2,1);
plot(x,sin(x)-1);
title(‘y=sinx-1’);axis([0,2pi,-2,1]);
subplot(2,1,2);
plot(x,cos(x)+1)
title(‘y=cosx+1’);axis([0,2*pi,0,2]);
subplot(4,4,3);
plot(x,tan(x))
title(‘y=tanx’);axis([-pi,pi,-5,5]);
subplot(4,4,8);
plot(x,cot(x))
title(‘y=cotx’);axis([-5,5,-pi,pi]);

5.3 其它形式的二维曲线

其他坐标系下的二维曲线：
（1）对数坐标图
semilogx(x1,y1,选项1,x2,y2,选项2……）
semilogy(x1,y1,选项1,x2,y2,选项2……）
loglog(x1,y1,选项1,x2,y2,选项2……）
eg1:绘制$\frac{1}{x}$的直角线形坐标图和三种对数坐标图。

x=1:0.1:10;
y=1./x;
subplot(2,2,1);
plot(x,y)
title('plot(x,y)');
subplot(2,2,2);
semilogx(x,y)
title('semilogx(x,y)');grid on
subplot(2,2,3);
semilogy(x,y)
title('semilogy(x,y)');grid on
subplot(2,2,4);
loglog(x,y)
title('loglog(x,y)');grid on

（2）极坐标图
polar(theta,rho,选项)
eg:按极坐标方程ρ=1-sinθ绘制心形曲线

t=0:pi/100:2*pi;
r=1-sin(t);
polar(t,r)

统计图
（1）条形类图形

①条形图：

• bar(y,style):y是数据，选项style用于指定分组排列模式
  style ----grouped：簇状分组 stacked：堆积分组
• barh(x,style) 换个方向

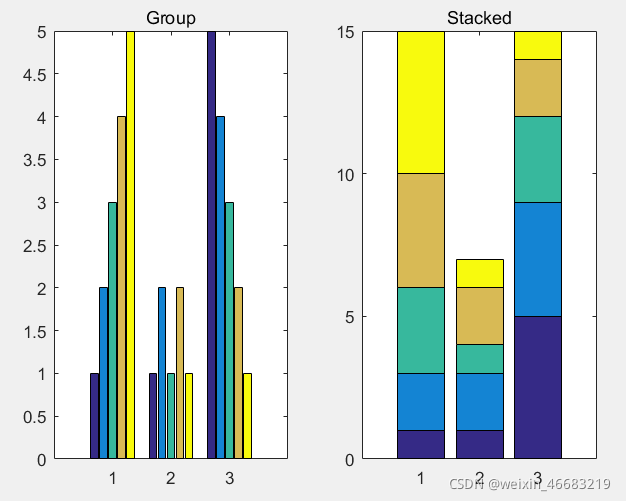
eg：绘制分组条形图

y=[1 2 3 4 5;1 2 1 2 1;5 4 3 2 1];
subplot(1,2,1)
bar(y)
title('Group')
subplot(1,2,2)
bar(y,'stacked')
title('Stacked')

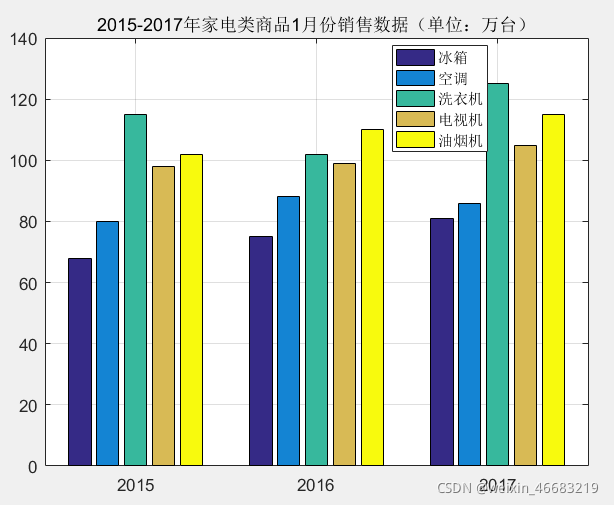
• bar(x,y,style) x存储横坐标，y存储数据

eg:

x=[2015 ,2016,2017];
y=[68 80 115 98 102;75 88 102 99 110;81 86 125 105 115];
bar(x,y)
title('2015-2017年家电类商品1月份销售数据（单位：万台）');grid on
legend('冰箱','空调','洗衣机','电视机','油烟机')

②直方图

• hist函数（直角坐标）:hist(y) hist(y,x) ------y是要统计的数据，x用于指定区间的划分方式

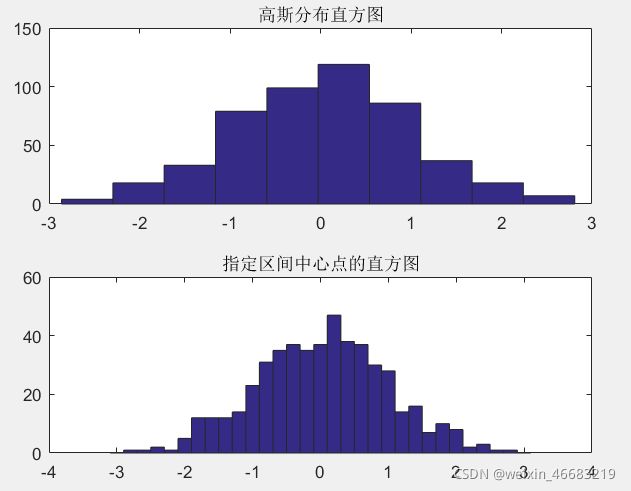
eg：绘制服从高斯分布的直方图。

y=randn(500,1); # 函数randn：产生均值为0，方差 σ^2 = 1，标准差σ = 1的正态分布的随机数或矩阵的函数。此处是500*1矩阵
subplot(2,1,1);
hist(y);
title('高斯分布直方图');
subplot(2,1,2)
x=-3:0.2:3;
hist(y,x);
title('指定区间中心点的直方图')

• rose函数（极坐标）
  rose（theta,x):theta角度，x指定区间的划分方式
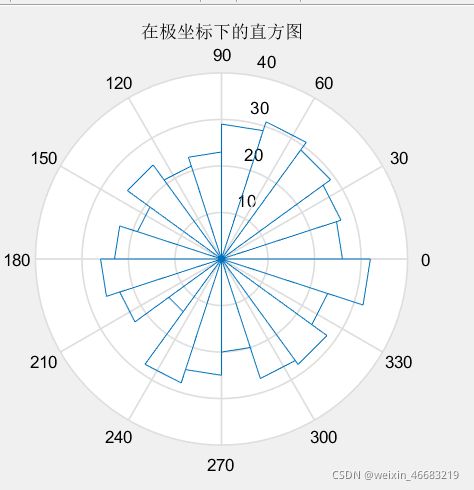
  eg：绘制高斯分布数据在极坐标的直方图

y=randn(500,1);
theta=y*pi; #由于theta以弧度为单位，所以转换成弧度
rose(theta)
title('在极坐标下的直方图')

（2）面积类图形

①扇形图
pie函数：pie(x,explode) x存储待统计数据，选项explode控制图块的显示模式
eg:某次考试优秀、良好、中等、及格、不及格的人数分别为：5 17 23 9 4，用扇形统计图作成绩统计分析

x=[5 17 23 9 4];
ex=[0 0 0 0 1]; #1表示突出显示第五块区域
pie(x,ex)
legend('优秀','良好','中等','及格','不及格','location','eastoutside')
# location设置图例位置，放在东侧图形外面

②面积图
area函数

（3)散点类图形

• scatter函数：散点图
  scatter(x,y,选项，’filled‘） x,y用于定位数据点，选项用于指定线形、颜色、数据点标记。
  eg：以散点图形式绘制桃心曲线，曲线的参数方程如下。
  $$\{\begin{array}{l}x=16si{n}^{3}t\\ y=13cost-5cos(2t)-2cos(3t)-cos(4t)\end{array}$$

t=0:pi/100:2*pi;
x=16*sin(t).^3;
y=13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t);
scatter(x,y,'rd','filled') #rd:红色棱形

• stairs函数：阶梯图
• stem函数：杆图

矢量类图形

• compass函数：罗盘图
• feather函数：羽毛图
• quiver函数：箭头图

quiver（x,y,u,v) 其中，（x,y)指定矢量起点，(u,v)指定矢量终点
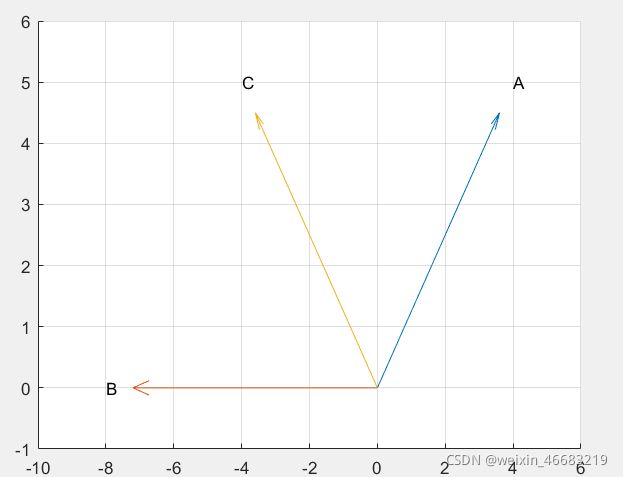
eg：已知向量A,B，求A+B，并用矢量图表示

A=[4,5];B=[-8,0];C=A+B;
hold on;
quiver(0,0,A(1),A(2));
quiver(0,0,B(1),B(2));
quiver(0,0,C(1),C(2));
text(A(1),A(2),'A');text(B(1),B(2),'B');text(C(1),C(2),'C');
axis([-10,6,-1,6]);
grid on