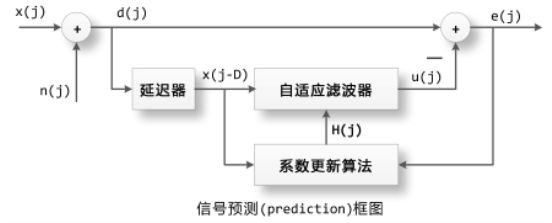
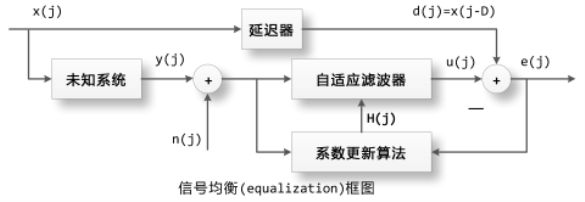
自适应滤波
应用:
公式:
自适应滤波器中最重要的一个环节就是其系数的更新算法,如果不对自适应滤波器的系数更新的话,那么它就只是一个普通的FIR滤波器了。系数更新算法有很多种类,最基本、常用、简单的一种方法叫做NLMS(归一化最小均方),让我们先来看看它的数学公式表达:
设置自适应滤波器系数h的所有初始值为0,h的长度为I。
对每个取样值进行如下计算,其中n=0, 1, 2, ...
自适应滤波器系数 ![]() 是一个长度为I的矢量,也就是一个长度为I的FIR滤波器。在时刻n,滤波器的每个系数对应的输入信号为
是一个长度为I的矢量,也就是一个长度为I的FIR滤波器。在时刻n,滤波器的每个系数对应的输入信号为 ![]() ,它也是一个长度为I的矢量。这两个矢量的点乘即为滤波器的输出和目标信号d(n)之间的差为e(n),然后根据e(n)和
,它也是一个长度为I的矢量。这两个矢量的点乘即为滤波器的输出和目标信号d(n)之间的差为e(n),然后根据e(n)和 ![]() , 更新滤波器的系数。
, 更新滤波器的系数。
数学公式总是令人难以理解的,下面我们以图示为例进行说明:
图中假设自适应滤波器h的长度为4,在时刻7滤波器的输出为:
u[7] = h[0]*x[7] + h[1]*x[6] + h[2]*x[5] + h[3]*x[4]
滤波器的输入信号的平方和powerX为:
powerX = x[4]*x[4] + x[5]*x[5] + x[6]*x[6] + x[7]*x[7]
未知系统的输出d[7]和滤波器的输出u[7]之间的差为:
e[7] = d[7] - u[7]
使用u[7]和x[4]..x[7]对滤波器的系数更新:
h[4] = h[4] + u * e[7]*x[4]/powerX
h[4] = h[5] + u * e[7]*x[5]/powerX
h[4] = h[6] + u * e[7]*x[6]/powerX
h[4] = h[7] + u * e[7]*x[7]/powerX
其中参数u成为更新系数,为0到1之间的一个实数,此值越大系数更新的速度越快。对于每个时刻i都需要进行上述的计算,因此滤波器的系数对于每个参照信号x的取样都更新一次。
参考:摘抄自《用Python做科学计算》http://sebug.net/paper/books/scipydoc/fast_nlms_in_python.html