4.数据结构（0x3f：从周赛中学算法 2022下）

来自0x3f【从周赛中学算法 - 2022 年周赛题目总结（下篇）】：https://leetcode.cn/circle/discuss/WR1MJP/

包括堆（优先队列）、单调栈、单调队列、字典树、并查集、树状数组、线段树等。

学习这些只是开始，能否灵活运用才是关键。

注：常见于周赛第四题（约占 21%）。

题目	难度	备注
2416. 字符串的前缀分数和	1725	字典树
2462. 雇佣 K 位工人的总代价	1764	最小堆
2398. 预算内的最多机器人数目	1917	双指针+单调队列
2426. 满足不等式的数对数目	2030	式子变形+逆序对模型+树状数组
2402. 会议室 III	2093	最小堆（双堆模拟）
2382. 删除操作后的最大子段和	2136	并查集
2454. 下一个更大元素 IV	2175	单调栈（双单调栈模拟）
2503. 矩阵查询可获得的最大分数	2196	离线询问+并查集/最小堆
2334. 元素值大于变化阈值的子数组	2381	并查集/单调栈
2421. 好路径的数目	2445	并查集

其他

题目	难度	备注
1172. 餐盘栈	1209	最小堆（懒删除堆）

灵神-从周赛中学算法（数据结构）

2416. 字符串的前缀分数和

难度困难36

给你一个长度为 n 的数组 words ，该数组由 非空 字符串组成。

定义字符串 word 的 分数 等于以 word 作为 前缀 的 words[i] 的数目。

• 例如，如果 words = ["a", "ab", "abc", "cab"] ，那么 "ab" 的分数是 2 ，因为 "ab" 是 "ab" 和 "abc" 的一个前缀。

返回一个长度为 n 的数组 answer ，其中 answer[i] 是 words[i] 的每个非空前缀的分数 总和 。

**注意：**字符串视作它自身的一个前缀。

示例 1：

输入：words = ["abc","ab","bc","b"]
输出：[5,4,3,2]
解释：对应每个字符串的答案如下：
- "abc" 有 3 个前缀："a"、"ab" 和 "abc" 。
- 2 个字符串的前缀为 "a" ，2 个字符串的前缀为 "ab" ，1 个字符串的前缀为 "abc" 。
总计 answer[0] = 2 + 2 + 1 = 5 。
- "ab" 有 2 个前缀："a" 和 "ab" 。
- 2 个字符串的前缀为 "a" ，2 个字符串的前缀为 "ab" 。
总计 answer[1] = 2 + 2 = 4 。
- "bc" 有 2 个前缀："b" 和 "bc" 。
- 2 个字符串的前缀为 "b" ，1 个字符串的前缀为 "bc" 。 
总计 answer[2] = 2 + 1 = 3 。
- "b" 有 1 个前缀："b"。
- 2 个字符串的前缀为 "b" 。
总计 answer[3] = 2 。

示例 2：

输入：words = ["abcd"]
输出：[4]
解释：
"abcd" 有 4 个前缀 "a"、"ab"、"abc" 和 "abcd"。
每个前缀的分数都是 1 ，总计 answer[0] = 1 + 1 + 1 + 1 = 4 。

提示：

• 1 <= words.length <= 1000
• 1 <= words[i].length <= 1000
• words[i] 由小写英文字母组成

题解：前缀树记录字符次数

class Solution {
    public int[] sumPrefixScores(String[] words) {
        Trie trie = new Trie();
        for(String w : words){
            trie.insert(w);
        }
        int n = words.length;
        int[] res = new int[n];
        for(int i = 0; i < n; i++){
            res[i] = trie.search(words[i]);
        }
        return res;
    }

    class Trie{
        class TrieNode{
            boolean end;
            int pass;
            TrieNode[] child;
            public TrieNode(){
                end = false;
                pass = 0;
                child = new TrieNode[26];
            }
        }
        
        TrieNode root;//字典树的根节点。
	
        public Trie() {
            root = new TrieNode();
        }

        public void insert(String s){
            TrieNode p = root;
            for(int i = 0; i < s.length(); i++){
                int u = s.charAt(i) - 'a';
                if(p.child[u] == null ) p.child[u] = new TrieNode();
                p = p.child[u];
                p.pass++;
            }
        }

        public int search(String s){
            TrieNode p = root;
            int tot = 0;
            for(int i = 0; i < s.length(); i++){
                int u = s.charAt(i) - 'a';
                p = p.child[u];
                tot += p.pass;
            }
            return tot;
        }
    }
}

2462. 雇佣 K 位工人的总代价

难度中等23

给你一个下标从 0 开始的整数数组 costs ，其中 costs[i] 是雇佣第 i 位工人的代价。

同时给你两个整数 k 和 candidates 。我们想根据以下规则恰好雇佣 k 位工人：

• 总共进行 k 轮雇佣，且每一轮恰好雇佣一位工人。
• 在每一轮雇佣中，从最前面 candidates 和最后面 candidates 人中选出代价最小的一位工人，如果有多位代价相同且最小的工人，选择下标更小的一位工人。
  • 比方说，costs = [3,2,7,7,1,2] 且 candidates = 2 ，第一轮雇佣中，我们选择第 4 位工人，因为他的代价最 小 [*3,2*,7,7,***1**,2*] 。
  • 第二轮雇佣，我们选择第 1 位工人，因为他们的代价与第 4 位工人一样都是最小代价，而且下标更小，[*3,**2***,7,*7,2*] 。注意每一轮雇佣后，剩余工人的下标可能会发生变化。
• 如果剩余员工数目不足 candidates 人，那么下一轮雇佣他们中代价最小的一人，如果有多位代价相同且最小的工人，选择下标更小的一位工人。
• 一位工人只能被选择一次。

返回雇佣恰好 k 位工人的总代价。

示例 1：

输入：costs = [17,12,10,2,7,2,11,20,8], k = 3, candidates = 4
输出：11
解释：我们总共雇佣 3 位工人。总代价一开始为 0 。
- 第一轮雇佣，我们从 [17,12,10,2,7,2,11,20,8] 中选择。最小代价是 2 ，有两位工人，我们选择下标更小的一位工人，即第 3 位工人。总代价是 0 + 2 = 2 。
- 第二轮雇佣，我们从 [17,12,10,7,2,11,20,8] 中选择。最小代价是 2 ，下标为 4 ，总代价是 2 + 2 = 4 。
- 第三轮雇佣，我们从 [17,12,10,7,11,20,8] 中选择，最小代价是 7 ，下标为 3 ，总代价是 4 + 7 = 11 。注意下标为 3 的工人同时在最前面和最后面 4 位工人中。
总雇佣代价是 11 。

示例 2：

输入：costs = [1,2,4,1], k = 3, candidates = 3
输出：4
解释：我们总共雇佣 3 位工人。总代价一开始为 0 。
- 第一轮雇佣，我们从 [1,2,4,1] 中选择。最小代价为 1 ，有两位工人，我们选择下标更小的一位工人，即第 0 位工人，总代价是 0 + 1 = 1 。注意，下标为 1 和 2 的工人同时在最前面和最后面 3 位工人中。
- 第二轮雇佣，我们从 [2,4,1] 中选择。最小代价为 1 ，下标为 2 ，总代价是 1 + 1 = 2 。
- 第三轮雇佣，少于 3 位工人，我们从剩余工人 [2,4] 中选择。最小代价是 2 ，下标为 0 。总代价为 2 + 2 = 4 。
总雇佣代价是 4 。

提示：

• 1 <= costs.length <= 105
• 1 <= costs[i] <= 105
• 1 <= k, candidates <= costs.length

题解：

• 情况一： candidates * 2 >= len 时，直接数组排序，取前 k 个数之和。
• 情况二： 否则，构建最小堆，双指针对撞来解（双指针相遇时，即转化为情况一）。

class Solution {
    public long totalCost(int[] costs, int k, int candidates) {
        long ans = 0l;
        int n = costs.length;
        // 直接排序 取前k个数之和
        if(candidates * 2 >= n){
            Arrays.sort(costs);
            for(int i = 0; i < k; i++){
                ans += costs[i];
            }
            return ans;
        }
        // 最小堆： 如果o1和o2位置的开销不相等的话，取对应的开销更小值；相等的话，取坐标的更小值。
        PriorityQueue<Integer> q = new PriorityQueue<>((o1, o2) -> {
            return costs[o1] != costs[o2] ? costs[o1] - costs[o2] : o1 - o2;
        });
        for(int i = 0; i < candidates; i++){
            q.add(i);
            q.add(n-1-i);
        }
        for(int l = candidates, r = n-1-candidates; k > 0; k--){
            int p = q.poll();
            ans += costs[p];
            //  当双指针相遇时，说明数组中所有元素都加入最小堆了，此时化为情况一，取值至k == 0
            if (l <= r){
                q.add(p < l ? l++ : r--);
            }
        }
        return ans;
    }
}

2398. 预算内的最多机器人数目

难度困难18

你有 n 个机器人，给你两个下标从 0 开始的整数数组 chargeTimes 和 runningCosts ，两者长度都为 n 。第 i 个机器人充电时间为 chargeTimes[i] 单位时间，花费 runningCosts[i] 单位时间运行。再给你一个整数 budget 。

运行 k 个机器人 总开销 是 max(chargeTimes) + k * sum(runningCosts) ，其中 max(chargeTimes) 是这 k 个机器人中最大充电时间，sum(runningCosts) 是这 k 个机器人的运行时间之和。

请你返回在 不超过 budget 的前提下，你 最多 可以 连续 运行的机器人数目为多少。

示例 1：

输入：chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], budget = 25
输出：3
解释：
可以在 budget 以内运行所有单个机器人或者连续运行 2 个机器人。
选择前 3 个机器人，可以得到答案最大值 3 。总开销是 max(3,6,1) + 3 * sum(2,1,3) = 6 + 3 * 6 = 24 ，小于 25 。
可以看出无法在 budget 以内连续运行超过 3 个机器人，所以我们返回 3 。

示例 2：

输入：chargeTimes = [11,12,19], runningCosts = [10,8,7], budget = 19
输出：0
解释：即使运行任何一个单个机器人，还是会超出 budget，所以我们返回 0 。

提示：

• chargeTimes.length == runningCosts.length == n
• 1 <= n <= 5 * 104
• 1 <= chargeTimes[i], runningCosts[i] <= 105
• 1 <= budget <= 1015

题解：https://leetcode.cn/problems/maximum-number-of-robots-within-budget/solution/by-endlesscheng-7ukp/

前置题目：239. 滑动窗口最大值。

在 239 这题的基础上，把固定大小的滑动窗口改为不固定大小的双指针

class Solution {
    // 在 不超过 budget 的前提下，你 最多 可以 【连续】 运行的机器人数目为多少
    // 维护一个单调队列 + 双指针，每次入队right，然后检查 不符合条件则退出left至符合条件
    public int maximumRobots(int[] chargeTimes, int[] runningCosts, long budget) {
        // 维护一个单调递增队列，队首元素 > 队尾元素值
        Deque<Integer> q = new ArrayDeque<>();
        int res = 0;
        long sum = 0l;
        // 枚举区间右端点 right，计算区间左端点 left 的最小值
        for(int left = 0, right = 0; right < chargeTimes.length; right++){
            // 及时清除队列中的无用数据，保证队列的单调性
            while(!q.isEmpty() && chargeTimes[right] >= chargeTimes[q.peekLast()]){
                q.pollLast();
            }
            q.addLast(right);
            sum += runningCosts[right];
            // 如果左端点 left 不满足要求，就不断右移 left
            while(!q.isEmpty() && 
                        chargeTimes[q.peekFirst()] + (right - left + 1) * sum > budget){
                // 及时清除队列中无用的数据，保证队列单调性
                if(q.peekFirst() == left) q.pollFirst();
                sum -= runningCosts[left++];
            }
            res = Math.max(res, right - left + 1);
        }
        return res;
    }
}

进阶：把「子数组」改成「子序列」要怎么做？

思路和 1383. 最大的团队表现值 是类似的。思考题的讲解见 视频讲解 的最后一部分

题解：

子序列 ==> 顺序无关性，先排序

枚举每位chargeTimes，在以chargeTimes[i]为最大max(chargeTimes)时，不超过 budget 的前提下 k * sum(runningCosts)的最大值，这可以用堆来维护

class Solution:
    def maximumRobotsSubseq(self, chargeTimes: List[int], runningCosts: List[int], budget: int) -> int:
        ans = sum_cost = 0
        h = []  # 最大堆，堆顶表示当前的最大花费，从而贪心地在不满足要求的情况下，优先去掉最大的花费
        for t, c in sorted(zip(chargeTimes, runningCosts)):  # 按照时间排序，从而保证当前的时间是最大的，在此之前的机器人都是可以选的
            heappush(h, -c)
            sum_cost += c
            while h and t + len(h) * sum_cost > budget:
                sum_cost += heappop(h)  # 弹出一个最大花费，即使弹出的是当前的 c 也没关系，这不会得到更大的 ans
            ans = max(ans, len(h))
        return ans

2426. 满足不等式的数对数目

难度困难15

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，两个数组的大小都为 n ，同时给你一个整数 diff ，统计满足以下条件的 数对 (i, j) ：

• 0 <= i < j <= n - 1 且
• nums1[i] - nums1[j] <= nums2[i] - nums2[j] + diff.

请你返回满足条件的 数对数目 。

示例 1：

输入：nums1 = [3,2,5], nums2 = [2,2,1], diff = 1
输出：3
解释：
总共有 3 个满足条件的数对：
1. i = 0, j = 1：3 - 2 <= 2 - 2 + 1 。因为 i < j 且 1 <= 1 ，这个数对满足条件。
2. i = 0, j = 2：3 - 5 <= 2 - 1 + 1 。因为 i < j 且 -2 <= 2 ，这个数对满足条件。
3. i = 1, j = 2：2 - 5 <= 2 - 1 + 1 。因为 i < j 且 -3 <= 2 ，这个数对满足条件。
所以，我们返回 3 。

示例 2：

输入：nums1 = [3,-1], nums2 = [-2,2], diff = -1
输出：0
解释：
没有满足条件的任何数对，所以我们返回 0 。

提示：

• n == nums1.length == nums2.length
• 2 <= n <= 105
• -104 <= nums1[i], nums2[i] <= 104
• -104 <= diff <= 104

题解：https://leetcode.cn/problems/number-of-pairs-satisfying-inequality/solution/by-endlesscheng-9prc/

树状数组/线段树逐渐成为周赛必备技能了。本题用到的技巧是，合并下标相同的元素。

因此本题和 剑指 Offer 51. 数组中的逆序对、315. 计算右侧小于当前元素的个数 等题目实质上是同一类题，用归并排序或者树状数组等均可以通过。

通常给的式子要变形：相同下标放一起，

nums1[i] - nums1[j] <= nums2[i] - nums2[j] + diff

==> nums1[i] - nums2[i] <= nums1[j] - nums2[j] + diff

然后设 a[i] = nums1[i] = nums2[i]，

则原式变为 a[i] <= a[j] + diff ==> 逆序对问题

解决逆序对问题：Ⅰ树状数组 Ⅱ 归并排序

逆序对问题的两种做法：树状数组&归并排序

方法一：树状数组+离散化

• 从左到右遍历a[i]，统计每个元素的出现次数，

本题中，统计 <= a[i] + diff，的元素个数，就是答案要求的数对个数，然后再把a[i]，加到统计到的数据结构里面。

我们需要一个数据结构，能够添加元素，并且查询 <= x的元素个数

• 能够满足的数据结构有：树状数组、线段树、名次树

---

离散化：离散化是在不改变数据相对大小的条件下,对数据进行相应的缩小

• 例如：原数据：1,999,100000,15；处理后：1,3,4,2；

class Solution {
    /**
    通常给的式子要变形：相同下标放一起，nums1[i] - nums1[j] <= nums2[i] - nums2[j] + diff
    ==> nums1[i] - nums2[i] <= nums1[j] - nums2[j] + diff
    设  a[i] = nums1[i] - nums2[i]
    则原式变为 a[i] <= a[j] + diff ==> 逆序对问题
    解决逆序对问题：Ⅰ树状数组 Ⅱ 归并排序

     */
    public long numberOfPairs(int[] a, int[] nums2, int diff) {
        int n = a.length;
        for (int i = 0; i < n; ++i)
            a[i] -= nums2[i]; // 设   a[i] = nums1[i] = nums2[i]
        // 由于a中存在负数，需要离散化，如果有相同元素，可以进行去重，例如
        // -3 2 2 5 6 7 ==>
        //  0 1   2 3 4 
        // 这样，在有序数组中查找 <= x + d 的元素个数时，可以进行二分
        int[] b = Arrays.stream(a).distinct().sorted().toArray();
        long ans = 0l;
        BinaryIndexedTree t = new BinaryIndexedTree(n);
        for(int x : a){
            // 有cnt个数 <= x + diff
            int cnt = lowerBound(b, x+diff+1); // 这里查询x+diff+1要加1（因为树状数组中下标从1开始，整体后移一位）

            // 查询树状数组中有多少个数，在遍历到x之前已经被添加了
            ans += t.query(cnt);
            t.add(lowerBound(b, x) + 1, 1); // 注意下标从1开始，整体后移
        }
        return ans;
    }
    
    // 查找小于等于x的元素个数
    public int lowerBound(int[] a, int x){
        int left = 0, right = a.length;
        while(left < right){
            int mid = left + (right - left) / 2;
            if(a[mid] < x) left = mid + 1;
            else right = mid;
        }
        return left;
    }
}

class BinaryIndexedTree{
    private int n;
    private int[] tree;

    public BinaryIndexedTree(int n){
        this.n = n;
        tree = new int[n + 1];
    }
    // 将index位置加上val值 arr[i] += val
    public void add(int index, int val){
        while(index <= n){
            tree[index] += val;
            index += index & -index;
        }
    }
    // 查询[0, index]的前缀和 sum(arr[:i+1])
    public int query(int index) {
        int s = 0;
        while (index > 0) {
            s += tree[index];
            index -= index & -index; // n&(~n+1) == n&(-n)
        }
        return s;
    }
	// 返回[left, right]之间的区间和
    public int RangeSum(int left, int right){
        return query(right+1) - query(left);
    }
}

方法二：归并排序的做法

class Solution {
    long res = 0;
    int[] tmp;
    public long numberOfPairs(int[] nums1, int[] nums2, int diff) {
        // nums1[i] - nums2[i] <= nums1[j] - nums2[j] + diff.
        // a[i] <= a[j] + diff
        int n = nums1.length;
        tmp = new int[n];//创建临时变量数组，用于两两有序区间进行筛选最小值排序的
        int[] a = new int[n];
        for(int i = 0; i < n; i++) a[i] = (nums1[i] - nums2[i]);
        mergeSort(a, diff, 0, n-1);
        return res;
    }

    public void mergeSort(int[] a, int diff, int left, int right){
        if(left >= right) return;
        int mid = left + (right - left) / 2;
        // 分解数组
        mergeSort(a, diff, left, mid);
        mergeSort(a, diff, mid + 1, right);

        // 此时数组a的下标 [left, mid] 和下标 [mid + 1, right] 范围内数组已然有序
        // 在这里进行逆序对的判断，收集满足条件的逆序对
        // 为什么不能和逆序对问题一样在合并的时候进行判断？ 
        // 				逆序对求a[i] > a[j]的数量，此问题求a[i] <= a[j]+diff的数量，不存在单调性？因此需要额外循环判断
        int i = left, j = mid + 1;
        while(j <= right){
            while(i <= mid && a[i] <= a[j] + diff){
                i++; // 满足条件的i，最后收集[left,i)
            }
            res += (i - left);
            j++;
        }

        // 进行合并，排序, 此时要对数组a的下标[left, right)范围内数组进行排序
        i = left; j = mid + 1;
        int k = left;
        while(i <= mid && j <= right){
            tmp[k++] = a[i] < a[j] ? a[i++] : a[j++];
        }
        while(i <= mid) tmp[k++] = a[i++];
        while(j <= right) tmp[k++] = a[j++];
        //将排序后的temp数组合并至原数组对应的索引部分
        for(int idx = left; idx <= right; idx++){
            a[idx] = tmp[idx];
        }
    }
}

剑指 Offer 51. 数组中的逆序对

难度困难996

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

class Solution {
    int res = 0;
    public int reversePairs(int[] nums) {
        mergeSort(nums, 0, nums.length - 1);
        return res;
    }

    public void mergeSort(int[] nums, int left, int right){
        if(left >= right) return;
        int mid = left + (right - left) / 2;
        mergeSort(nums, left, mid);
        mergeSort(nums, mid + 1, right);
        // 此时数组a的下标 [left, mid] 和下标 [mid + 1, right] 范围内数组已然有序
        // 合并数组，使得[left, right]有序
        int[] tmp = new int[right - left + 1];
        int i = left, j = mid + 1;
        int k = 0;
        while(i <= mid && j <= right){
            if(nums[i] <= nums[j]) tmp[k++] = nums[i++];
            else{
                res += (mid - i + 1); // a[i:mid+1] 中的元素都比a[j]大
                tmp[k++] = nums[j++];
            }
        }
        while(i <= mid) tmp[k++] = nums[i++];
        while(j <= right) tmp[k++] = nums[j++];
        for(int cur = 0; cur < right - left + 1; cur++){
            nums[left + cur] = tmp[cur];
        }
    }
}

2402. 会议室 III

难度困难28

给你一个整数 n ，共有编号从 0 到 n - 1 的 n 个会议室。

给你一个二维整数数组 meetings ，其中 meetings[i] = [starti, endi] 表示一场会议将会在 半闭 时间区间 [starti, endi) 举办。所有 starti 的值 互不相同 。

会议将会按以下方式分配给会议室：

1. 每场会议都会在未占用且编号 最小 的会议室举办。
2. 如果没有可用的会议室，会议将会延期，直到存在空闲的会议室。延期会议的持续时间和原会议持续时间 相同 。
3. 当会议室处于未占用状态时，将会优先提供给原 开始 时间更早的会议。

返回举办最多次会议的房间 编号 。如果存在多个房间满足此条件，则返回编号 最小 的房间。

半闭区间 [a, b) 是 a 和 b 之间的区间，包括 a 但 不包括 b 。

示例 1：

输入：n = 2, meetings = [[0,10],[1,5],[2,7],[3,4]]
输出：0
解释：
- 在时间 0 ，两个会议室都未占用，第一场会议在会议室 0 举办。
- 在时间 1 ，只有会议室 1 未占用，第二场会议在会议室 1 举办。
- 在时间 2 ，两个会议室都被占用，第三场会议延期举办。
- 在时间 3 ，两个会议室都被占用，第四场会议延期举办。
- 在时间 5 ，会议室 1 的会议结束。第三场会议在会议室 1 举办，时间周期为 [5,10) 。
- 在时间 10 ，两个会议室的会议都结束。第四场会议在会议室 0 举办，时间周期为 [10,11) 。
会议室 0 和会议室 1 都举办了 2 场会议，所以返回 0 。 

示例 2：

输入：n = 3, meetings = [[1,20],[2,10],[3,5],[4,9],[6,8]]
输出：1
解释：
- 在时间 1 ，所有三个会议室都未占用，第一场会议在会议室 0 举办。
- 在时间 2 ，会议室 1 和 2 未占用，第二场会议在会议室 1 举办。
- 在时间 3 ，只有会议室 2 未占用，第三场会议在会议室 2 举办。
- 在时间 4 ，所有三个会议室都被占用，第四场会议延期举办。 
- 在时间 5 ，会议室 2 的会议结束。第四场会议在会议室 2 举办，时间周期为 [5,10) 。
- 在时间 6 ，所有三个会议室都被占用，第五场会议延期举办。 
- 在时间 10 ，会议室 1 和 2 的会议结束。第五场会议在会议室 1 举办，时间周期为 [10,12) 。 
会议室 1 和会议室 2 都举办了 2 场会议，所以返回 1 。 

提示：

• 1 <= n <= 100
• 1 <= meetings.length <= 105
• meetings[i].length == 2
• 0 <= starti < endi <= 5 * 105
• starti 的所有值 互不相同

class Solution {
    public int mostBooked(int n, int[][] meetings) {
        int[] cnt = new int[n];
        //构造空闲会议室的小根堆 
        PriorityQueue<Integer> idle = new PriorityQueue<>();
        for(int i = 0; i < n; i++) idle.offer(i);
        //using存放使用中的会议室，key：结束时间，value：使用的会议室号(按照结束时间从小到大排序，相等则按照会议室号从小到大排序)
        PriorityQueue<Pair<Long, Integer>> using = new PriorityQueue<Pair<Long, Integer>>((a, b) -> 
            !Objects.equals(a.getKey(), b.getKey()) ? 
                Long.compare(a.getKey(), b.getKey()) : Integer.compare(a.getValue(), b.getValue()));
        Arrays.sort(meetings, (a, b) -> Integer.compare(a[0], b[0]));//按照时间由小到大排序 a[0] - b[0]
        for(int[] m : meetings){
            long st = m[0], end = m[1];
            // 维护在 st 时刻空闲的会议室(将所有结束了的会议室放到空闲idle堆去)
            while(!using.isEmpty() && using.peek().getKey() <= st){
                idle.offer(using.poll().getValue());
            }
            int id;
            // 没有可用的会议室，那么弹出一个最早结束的会议室（若有多个同时结束的，会弹出下标最小的）
            if(idle.isEmpty()){
                Pair<Long, Integer> p = using.poll();
                end += p.getKey()-st; // 更新当前会议的结束时间（添加上等待时间）
                id = p.getValue();
            }else id = idle.poll(); //有可用会议室，弹出栈顶
            cnt[id]++;
            using.offer(new Pair<>(end, id)); //处理当前会议，使用一个会议室
        }
        int ans = 0;
        for(int i = 0; i < n; i++) 
            if(cnt[ans] < cnt[i]) ans = i;
        return ans;
    }
}

2382. 删除操作后的最大子段和

难度困难25

给你两个下标从 0 开始的整数数组 nums 和 removeQueries ，两者长度都为 n 。对于第 i 个查询，nums 中位于下标 removeQueries[i] 处的元素被删除，将 nums 分割成更小的子段。

一个 子段 是 nums 中连续 正 整数形成的序列。子段和 是子段中所有元素的和。

请你返回一个长度为 n 的整数数组 answer ，其中 answer[i]是第 i 次删除操作以后的 最大 子段和。

**注意：**一个下标至多只会被删除一次。

示例 1：

输入：nums = [1,2,5,6,1], removeQueries = [0,3,2,4,1]
输出：[14,7,2,2,0]
解释：用 0 表示被删除的元素，答案如下所示：
查询 1 ：删除第 0 个元素，nums 变成 [0,2,5,6,1] ，最大子段和为子段 [2,5,6,1] 的和 14 。
查询 2 ：删除第 3 个元素，nums 变成 [0,2,5,0,1] ，最大子段和为子段 [2,5] 的和 7 。
查询 3 ：删除第 2 个元素，nums 变成 [0,2,0,0,1] ，最大子段和为子段 [2] 的和 2 。
查询 4 ：删除第 4 个元素，nums 变成 [0,2,0,0,0] ，最大子段和为子段 [2] 的和 2 。
查询 5 ：删除第 1 个元素，nums 变成 [0,0,0,0,0] ，最大子段和为 0 ，因为没有任何子段存在。
所以，我们返回 [14,7,2,2,0] 。

示例 2：

输入：nums = [3,2,11,1], removeQueries = [3,2,1,0]
输出：[16,5,3,0]
解释：用 0 表示被删除的元素，答案如下所示：
查询 1 ：删除第 3 个元素，nums 变成 [3,2,11,0] ，最大子段和为子段 [3,2,11] 的和 16 。
查询 2 ：删除第 2 个元素，nums 变成 [3,2,0,0] ，最大子段和为子段 [3,2] 的和 5 。
查询 3 ：删除第 1 个元素，nums 变成 [3,0,0,0] ，最大子段和为子段 [3] 的和 3 。
查询 5 ：删除第 0 个元素，nums 变成 [0,0,0,0] ，最大子段和为 0 ，因为没有任何子段存在。
所以，我们返回 [16,5,3,0] 。

提示：

• n == nums.length == removeQueries.length
• 1 <= n <= 105
• 1 <= nums[i] <= 109
• 0 <= removeQueries[i] < n
• removeQueries 中所有数字 互不相同 。

class Solution {
    // 删除不好做 ==> 逆序转换成添加 ==> 用并查集合并区间
    // 为什么不需要连接x,x-1?
    // 合并都是往右合并的 x的结果会保留在x+1 就相当于已经合并了左边
    // ans[i] 要么取上一个ans[i+1] 的最大子段和，要么取合并后的子段和，这两者取最大值。
    public long[] maximumSegmentSum(int[] nums, int[] removeQueries) {
        int n = nums.length;
        parent = new int[n+1];
        for(int i = 0; i <= n; i++) parent[i] = i;
        long[] sum = new long[n+1];
        long[] res = new long[n];
        res[n-1] = 0;
        for(int i = n-1; i > 0; i--){
            int idx = removeQueries[i]; // 添加的下标idx
            union(idx, idx+1);
            int to = parent[idx];
            sum[to] += nums[idx] + sum[idx];
            res[i-1] = Math.max(sum[to], res[i]); // i位置合并后，计算i-1位置的值
        }
        return res;
    }

    int[] parent;
    public void union(int x ,int y){
        int a = find(x);
        int b = find(y);
        if(a != b){
            parent[a] = b;
        }
    }

    public int find(int x){
        if(parent[x] != x) parent[x] = find(parent[x]);
        return parent[x];
    }
}

2454. 下一个更大元素 IV

难度困难27收藏分享切换为英文接收动态反馈

给你一个下标从 0 开始的非负整数数组 nums 。对于 nums 中每一个整数，你必须找到对应元素的 第二大 整数。

如果 nums[j] 满足以下条件，那么我们称它为 nums[i] 的 第二大 整数：

• j > i
• nums[j] > nums[i]
• 恰好存在 一个 k 满足 i < k < j 且 nums[k] > nums[i] 。

如果不存在 nums[j] ，那么第二大整数为 -1 。

• 比方说，数组 [1, 2, 4, 3] 中，1 的第二大整数是 4 ，2 的第二大整数是 3 ，3 和 4 的第二大整数是 -1 。

请你返回一个整数数组 answer ，其中 answer[i]是 nums[i] 的第二大整数。

示例 1：

输入：nums = [2,4,0,9,6]
输出：[9,6,6,-1,-1]
解释：
下标为 0 处：2 的右边，4 是大于 2 的第一个整数，9 是第二个大于 2 的整数。
下标为 1 处：4 的右边，9 是大于 4 的第一个整数，6 是第二个大于 4 的整数。
下标为 2 处：0 的右边，9 是大于 0 的第一个整数，6 是第二个大于 0 的整数。
下标为 3 处：右边不存在大于 9 的整数，所以第二大整数为 -1 。
下标为 4 处：右边不存在大于 6 的整数，所以第二大整数为 -1 。
所以我们返回 [9,6,6,-1,-1] 。

示例 2：

输入：nums = [3,3]
输出：[-1,-1]
解释：
由于每个数右边都没有更大的数，所以我们返回 [-1,-1] 。

提示：

• 1 <= nums.length <= 105
• 0 <= nums[i] <= 109

https://leetcode.cn/problems/next-greater-element-iv/solution/by-endlesscheng-q6t5/

class Solution {
    /**
    1. 需要两个数据结构，存储遍历过的数
        s存储遍历过的数
        t 存储遍历过，且这个数在右侧发现了比他大的数
    2. 单调递减的栈来实现 s 和 t
     */
    public int[] secondGreaterElement(int[] nums) {
        int n = nums.length;
        int[] res = new int[n];
        Arrays.fill(res, -1);
        // 模拟两个单调递减的栈，栈中的元素是下标
        Deque<Integer> s = new ArrayDeque<>();
        Deque<Integer> t = new ArrayDeque<>();
        for(int i = 0; i < n; i++){
            // 循环中先判断t，再判断s（若先判断s，则s中可能有元素转移到t，不符合条件）
            // 弹出比当前值小的元素值（找到了第二大的元素）
            while(!t.isEmpty() && nums[t.peek()] < nums[i]){
                res[t.pop()] = nums[i];
            }
            // s是递减栈(元素值从大到小),如果直接push进t中大小顺序会发生变化
            // 将s中元素挪到t中也应该是递减的，因此需要辅助栈tmp来帮忙
            Deque<Integer> tmp = new ArrayDeque<>();
            while(!s.isEmpty() && nums[s.peek()] < nums[i]){
                tmp.push(s.pop());
            }
            while(!tmp.isEmpty()){
                t.push(tmp.pop());
            }
            s.push(i);
        }
        return res;
    }
}

496. 下一个更大元素 I(Next Greater Number 一类问题)

难度简单1003

nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。

给你两个 没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。

对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。

返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的 下一个更大元素 。

示例 1：

输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 4 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
- 1 ，用加粗斜体标识，nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。

示例 2：

输入：nums1 = [2,4], nums2 = [1,2,3,4].
输出：[3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 2 ，用加粗斜体标识，nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ，用加粗斜体标识，nums2 = [1,2,3,4]。不存在下一个更大元素，所以答案是 -1 。

提示：

• 1 <= nums1.length <= nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 104
• nums1和nums2中所有整数 互不相同
• nums1 中的所有整数同样出现在 nums2 中

【单调栈解决 Next Greater Number 一类问题】：https://leetcode.cn/problems/next-greater-element-i/solution/dan-diao-zhan-jie-jue-next-greater-number-yi-lei-w/

首先，讲解 Next Greater Number 的原始问题：给你一个数组，返回一个等长的数组，对应索引存储着下一个更大元素，如果没有更大的元素，就存 -1。不好用语言解释清楚，直接上一个例子：

给你一个数组 [2,1,2,4,3]，你返回数组 [4,2,4,-1,-1]。

解释：第一个 2 后面比 2 大的数是 4; 1 后面比 1 大的数是 2；第二个 2 后面比 2 大的数是 4; 4 后面没有比 4 大的数，填 -1；3 后面没有比 3 大的数，填 -1。

这个问题可以这样抽象思考：把数组的元素想象成并列站立的人，元素大小想象成人的身高。这些人面对你站成一列，如何求元素「2」的 Next Greater Number 呢？很简单，如果能够看到元素「2」，那么他后面可见的第一个人就是「2」的 Next Greater Number，因为比「2」小的元素身高不够，都被「2」挡住了，第一个露出来的就是答案。

vector nextGreaterElement(vector& nums) {
    vector ans(nums.size()); // 存放答案的数组
    stack s;
    for (int i = nums.size() - 1; i >= 0; i--) { // 倒着往栈里放
        while (!s.empty() && s.top() <= nums[i]) { // 判定个子高矮
            s.pop(); // 矮个起开，反正也被挡着了。。。
        }
        ans[i] = s.empty() ? -1 : s.top(); // 这个元素身后的第一个高个
        s.push(nums[i]); // 进队，接受之后的身高判定吧！
    }
    return ans;
}

这就是单调队列解决问题的模板。for 循环要从后往前扫描元素，因为我们借助的是栈的结构，倒着入栈，其实是正着出栈。while 循环是把两个“高个”元素之间的元素排除，因为他们的存在没有意义，前面挡着个“更高”的元素，所以他们不可能被作为后续进来的元素的 Next Great Number 了。

---

给你一个数组 T = [73, 74, 75, 71, 69, 72, 76, 73]，这个数组存放的是近几天的天气气温（这气温是铁板烧？不是的，这里用的华氏度）。你返回一个数组，计算：对于每一天，你还要至少等多少天才能等到一个更暖和的气温；如果等不到那一天，填 0 。

举例：给你 T = [73, 74, 75, 71, 69, 72, 76, 73]，你返回 [1, 1, 4, 2, 1, 1, 0, 0]。

解释：第一天 73 华氏度，第二天 74 华氏度，比 73 大，所以对于第一天，只要等一天就能等到一个更暖和的气温。后面的同理。

你已经对 Next Greater Number 类型问题有些敏感了，这个问题本质上也是找 Next Greater Number，只不过现在不是问你 Next Greater Number 是多少，而是问你当前距离 Next Greater Number 的距离而已。

相同类型的问题，相同的思路，直接调用单调栈的算法模板，稍作改动就可以啦，直接上代码把。

vector dailyTemperatures(vector& T) {
    vector ans(T.size());
    stack s; // 这里放元素索引，而不是元素
    for (int i = T.size() - 1; i >= 0; i--) {
        while (!s.empty() && T[s.top()] <= T[i]) {
            s.pop();
        }
        ans[i] = s.empty() ? 0 : (s.top() - i); // 得到索引间距
        s.push(i); // 加入索引，而不是元素
    }
    return ans;
}

本题题解

class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i < nums1.length; i++)
            map.put(nums1[i], i);
        int[] res = new int[nums1.length];
        Arrays.fill(res, -1);
        Deque<Integer> dq = new ArrayDeque<>(); // 维护一个单调递减栈
        for(int i = 0; i < nums2.length; i++){
            int x = nums2[i];
            while(!dq.isEmpty() && nums2[dq.peek()] <= x){
                // 找到了dq.peek()位置的下一个更大的元素
                if(map.containsKey(nums2[dq.peek()])){
                    res[map.get(nums2[dq.peek()])] = x;
                }
                dq.pop();
            }
            dq.push(i);
        }
        return res;
    }
}

相似题目：

496.下一个更大元素I

503.下一个更大元素II

1118.一月有多少天

---

2503. 矩阵查询可获得的最大分数

难度困难34

给你一个大小为 m x n 的整数矩阵 grid 和一个大小为 k 的数组 queries 。

找出一个大小为 k 的数组 answer ，且满足对于每个整数 queres[i] ，你从矩阵 左上角 单元格开始，重复以下过程：

• 如果 queries[i] 严格 大于你当前所处位置单元格，如果该单元格是第一次访问，则获得 1 分，并且你可以移动到所有 4 个方向（上、下、左、右）上任一 相邻 单元格。
• 否则，你不能获得任何分，并且结束这一过程。

在过程结束后，answer[i] 是你可以获得的最大分数。注意，对于每个查询，你可以访问同一个单元格 多次 。

返回结果数组 answer 。

示例 1：

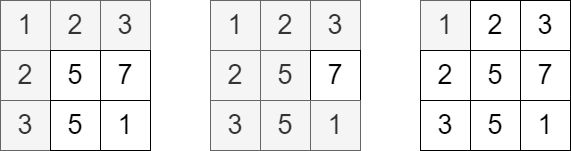
输入：grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
输出：[5,8,1]
解释：上图展示了每个查询中访问并获得分数的单元格。

示例 2：

输入：grid = [[5,2,1],[1,1,2]], queries = [3]
输出：[0]
解释：无法获得分数，因为左上角单元格的值大于等于 3 。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• k == queries.length
• 1 <= k <= 104
• 1 <= grid[i][j], queries[i] <= 106

class Solution {
    private static final int[][] dirs = {{-1, 0}, {0, 1}, {0, -1}, {1,0}};
    private int[] parent,size;
    public int[] maxPoints(int[][] grid, int[] queries) {
        int m = grid.length, n = grid[0].length, mn = m * n;
        // 并查集初始化
        parent = new int[mn];
        for(int i = 0; i < mn; i++) parent[i] = i;
        size = new int[mn];
        Arrays.fill(size, 1);

        // 矩阵元素从小到大排序，方便离线查询
        int[][] a = new int[mn][3];
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                a[i*n + j] = new int[]{grid[i][j], i, j};
            }
        }
        Arrays.sort(a, (p, q) -> p[0] - q[0]); 

        // 查询的下标按照查询值从小到大排序，方便离线
        int k = queries.length;
        Integer[] id = IntStream.range(0, k).boxed().toArray(Integer[]::new);
        Arrays.sort(id, (i, j) -> queries[i] - queries[j]);

        int[] ans = new int[k];
        int j = 0;
        for(int i : id){
            int q = queries[i]; // 限定值limit
            while(j < mn && a[j][0] < q){
                int x = a[j][1], y = a[j][2]; 
                //将(x,y)点与四个格子连接起来，前提是符合条件
                for(int[] d : dirs){
                    int nx = x + d[0], ny = y + d[1];
                    if(0 <= nx && nx < m && 0 <= ny && ny < n && grid[nx][ny] < q){
                        union(x*n + y, nx*n + ny);// 把坐标压缩成一维的编号
                    }
                }
                j++;
            }
            if(grid[0][0] < q){
                ans[i] = size[find(0)];// 左上角的连通块的大小
            }
        }
        return ans;
    }

    private void union(int x, int y){
        int a = find(x);
        int b = find(y);
        if(a != b){
            parent[b] = a;
            size[a] += size[b];
        }
    }

    private int find(int x){
        if(x != parent[x]) parent[x] = find(parent[x]);
        return parent[x];
    }
}

2334. 元素值大于变化阈值的子数组

难度困难31

给你一个整数数组 nums 和一个整数 threshold 。

找到长度为 k 的 nums 子数组，满足数组中 每个 元素都 大于 threshold / k 。

请你返回满足要求的 任意 子数组的 大小 。如果没有这样的子数组，返回 -1 。

子数组 是数组中一段连续非空的元素序列。

示例 1：

输入：nums = [1,3,4,3,1], threshold = 6
输出：3
解释：子数组 [3,4,3] 大小为 3 ，每个元素都大于 6 / 3 = 2 。
注意这是唯一合法的子数组。

示例 2：

输入：nums = [6,5,6,5,8], threshold = 7
输出：1
解释：子数组 [8] 大小为 1 ，且 8 > 7 / 1 = 7 。所以返回 1 。
注意子数组 [6,5] 大小为 2 ，每个元素都大于 7 / 2 = 3.5 。
类似的，子数组 [6,5,6] ，[6,5,6,5] ，[6,5,6,5,8] 都是符合条件的子数组。
所以返回 2, 3, 4 和 5 都可以。

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i], threshold <= 109

方法一：并查集

class Solution {
    // 满足数组中 每个 元素都 大于 threshold / k
    /**
        1. 数组中的元素越大越好，从大往小考虑nums[i]
        2. 数组长度k 越大越好，threshold / k就越小，越能满足要求
        3. 把考虑过的元素都串起来，这条链的长度就是k，如何维护？
        4. 并查集，遍历到nums[i]时，用并查集合并i 和 i+1，这样可以把连续访问过的位置串起来，同时维护链的长度。
     */
    int[] fa;
    public int validSubarraySize(int[] nums, int threshold) {
        int n = nums.length;
        fa = new int[n+1];
        for(int i = 0; i <= n; i++) fa[i] = i;
        // 维护一下每个集合的大小，一开始都是1
        int[] sz = new int[n+1];

        // 将数组中的元素下标从大到小排序，遍历时从大到小排序
        Integer[] ids = IntStream.range(0, n).boxed().toArray(Integer[]::new);
        Arrays.sort(ids, (i, j) -> nums[j] - nums[i]);

        for(int i : ids){
            // 此时i的fa肯定是自己，查看 i+1 的根节点，然后合并并维护集合大小
            int j = find(i+1);
            fa[i] = j; // 合并i 和 i+1
            sz[j] += sz[i] + 1; // 将 i 的区间长度和 i+1 的区间长度合并,加上i位置初始值的1
            // 判断是否满足条件
            if(nums[i] > threshold / sz[j]) return sz[j]; 
        }
        return -1;
    }
    // 返回x所在集合根节点（对本题来说是链的最右端）
    public int find(int x) {
        if (fa[x] != x) fa[x] = find(fa[x]);
        return fa[x];
    }

}

方法二：单调栈

class Solution {
    /**
        枚举每个元素，假设它是子数组的最小值
        子数组的左右边界最远能到哪？
        用单调栈来计算左右边界。
        
        单调栈的应用:不妨枚举nums[i]并假设某包含nums[i]的子段是长度为k的某段中最小的数字
        在该段中其余数字都大于nums[i]，只要nums[i]>threshold/k，那么段内的所有元素均大于threshold/k
        我们只需要求出有没有这样的nums[i]就可以知道是否有符合题意的k
        怎样维护某个nums[i]在某个段内是最小的数字？我们只需要找到nums[i]左边和右边首个严格小于nums[i]的索引
        那么索引之间就是nums[i]这段的波及范围
        快速求nums[i]左边和右边首个小于nums[i]的元素属于Next Greater问题，可以用单调栈解决
        时间复杂度：O(N) 空间复杂度：O(N)
     */
    public int validSubarraySize(int[] nums, int threshold) {
        int n = nums.length;
        int[] left = new int[n]; // left[i] 为左侧小于 nums[i] 的最近元素位置（不存在时为 -1）
        Deque<Integer> st = new ArrayDeque<Integer>(); // 维护一个单调递减栈（栈顶是最小值的下标）
        for(int i = 0; i < n; i++){
            while(!st.isEmpty() && nums[st.peek()] >= nums[i]) st.pop();
            left[i] = st.isEmpty() ? -1 : st.peek();
            st.push(i);
        }
        int[] right = new int[n]; // right[i] 为右侧小于 nums[i] 的最近元素位置（不存在时为 n）
        st = new ArrayDeque<>();
        for(int i = n-1; i >= 0; i--){
            while(!st.isEmpty() && nums[st.peek()] >= nums[i]) st.pop();
            right[i] = st.isEmpty() ? n : st.peek();
            st.push(i);
        }
        
        for(int i = 0; i < n; i++){
            // k ： 以nums[i]为区间最小值的区间长度
            // 右边界：right[i]-1 ； 左边界：left[i]+1
            // 子数组大小(right[i]-1) - (left[i] +1) + 1 ==> right[i] - left[i] - 1
            int k = right[i] - left[i] - 1;
            if(nums[i] > threshold / k) return k;
        }
        return -1;
    }
}

2421. 好路径的数目

难度困难70

给你一棵 n 个节点的树（连通无向无环的图），节点编号从 0 到 n - 1 且恰好有 n - 1 条边。

给你一个长度为 n 下标从 0 开始的整数数组 vals ，分别表示每个节点的值。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。

一条 好路径 需要满足以下条件：

1. 开始节点和结束节点的值 相同 。
2. 开始节点和结束节点中间的所有节点值都 小于等于 开始节点的值（也就是说开始节点的值应该是路径上所有节点的最大值）。

请你返回不同好路径的数目。

注意，一条路径和它反向的路径算作 同一 路径。比方说， 0 -> 1 与 1 -> 0 视为同一条路径。单个节点也视为一条合法路径。

示例 1：

输入：vals = [1,3,2,1,3], edges = [[0,1],[0,2],[2,3],[2,4]]
输出：6
解释：总共有 5 条单个节点的好路径。
还有 1 条好路径：1 -> 0 -> 2 -> 4 。
（反方向的路径 4 -> 2 -> 0 -> 1 视为跟 1 -> 0 -> 2 -> 4 一样的路径）
注意 0 -> 2 -> 3 不是一条好路径，因为 vals[2] > vals[0] 。

示例 2：

输入：vals = [1,1,2,2,3], edges = [[0,1],[1,2],[2,3],[2,4]]
输出：7
解释：总共有 5 条单个节点的好路径。
还有 2 条好路径：0 -> 1 和 2 -> 3 。

示例 3：

输入：vals = [1], edges = []
输出：1
解释：这棵树只有一个节点，所以只有一条好路径。

提示：

• n == vals.length
• 1 <= n <= 3 * 104
• 0 <= vals[i] <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges 表示一棵合法的树。

class Solution {
    // 开始节点的值应该是路径上所有节点的最大值
    
    // 从大到小超时&有删除操作->反着来删除变合并->并查集
    int[] parent;
    public int numberOfGoodPaths(int[] vals, int[][] edges) {
        int n = vals.length;
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int[] e : edges){
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x); // 建图
        }

        parent = new int[n];
        for(int i = 0; i < n; i++) parent[i] = i;
        // size[x] 表示节点值等于 vals[x] 的节点个数，
        // 如果按照节点值从小到大合并，size[x] 也是连通块内的等于最大节点值的节点个数
        int[] size = new int[n];
        Arrays.fill(size, 1);
        // 查询的下标按照查询值从小到大排序
        var id = IntStream.range(0, n).boxed().toArray(Integer[]::new);
        Arrays.sort(id, (i, j) -> vals[i] - vals[j]);

        int ans = n;
        for(int x : id){
            int vx = vals[x], fx = find(x);
            for(int y : g[x]){
                y = find(y);
                if(y == fx || vals[y] > vx) 
                    continue;// 只考虑最大节点值比 vx 小的连通块
                if(vals[y] == vx){ // 可以构成好路径
                    ans += size[fx] * size[y]; // 乘法原理
                    size[fx] += size[y]; // 统计连通块内节点值等于 vx 的节点个数
                }
                parent[y] = fx; // 把小的节点值合并到大的节点值上
            } 
        }
        return ans;
    }

    int find(int x){
        if(parent[x] != x) parent[x] = find(parent[x]);
        return parent[x];
    }
}

其他

1172. 餐盘栈

难度困难48

我们把无限数量 ∞ 的栈排成一行，按从左到右的次序从 0 开始编号。每个栈的的最大容量 capacity 都相同。

实现一个叫「餐盘」的类 DinnerPlates：

• DinnerPlates(int capacity) - 给出栈的最大容量 capacity。
• void push(int val) - 将给出的正整数 val 推入 从左往右第一个 没有满的栈。
• int pop() - 返回 从右往左第一个 非空栈顶部的值，并将其从栈中删除；如果所有的栈都是空的，请返回 -1。
• int popAtStack(int index) - 返回编号 index 的栈顶部的值，并将其从栈中删除；如果编号 index 的栈是空的，请返回 -1。

示例：

输入： 
["DinnerPlates","push","push","push","push","push","popAtStack","push","push","popAtStack","popAtStack","pop","pop","pop","pop","pop"]
[[2],[1],[2],[3],[4],[5],[0],[20],[21],[0],[2],[],[],[],[],[]]
输出：
[null,null,null,null,null,null,2,null,null,20,21,5,4,3,1,-1]

解释：
DinnerPlates D = DinnerPlates(2);  // 初始化，栈最大容量 capacity = 2
D.push(1);
D.push(2);
D.push(3);
D.push(4);
D.push(5);         // 栈的现状为：    2  4
                                    1  3  5
                                    ﹈ ﹈ ﹈
D.popAtStack(0);   // 返回 2。栈的现状为：      4
                                          1  3  5
                                          ﹈ ﹈ ﹈
D.push(20);        // 栈的现状为：  20  4
                                   1  3  5
                                   ﹈ ﹈ ﹈
D.push(21);        // 栈的现状为：  20  4 21
                                   1  3  5
                                   ﹈ ﹈ ﹈
D.popAtStack(0);   // 返回 20。栈的现状为：       4 21
                                            1  3  5
                                            ﹈ ﹈ ﹈
D.popAtStack(2);   // 返回 21。栈的现状为：       4
                                            1  3  5
                                            ﹈ ﹈ ﹈ 
D.pop()            // 返回 5。栈的现状为：        4
                                            1  3 
                                            ﹈ ﹈  
D.pop()            // 返回 4。栈的现状为：    1  3 
                                           ﹈ ﹈   
D.pop()            // 返回 3。栈的现状为：    1 
                                           ﹈   
D.pop()            // 返回 1。现在没有栈。
D.pop()            // 返回 -1。仍然没有栈。

提示：

• 1 <= capacity <= 20000
• 1 <= val <= 20000
• 0 <= index <= 100000
• 最多会对 push，pop，和 popAtStack 进行 200000 次调用。

超时，暴力做法

暴力做法的缺点，每次push和pop时都从端点开始找栈，有没有数据结构能帮我维护未满的栈

class DinnerPlates {

    List<Deque<Integer>> list;
    int capacity;

    public DinnerPlates(int capacity) {
        list = new ArrayList<>();
        this.capacity = capacity;
    }
    
    public void push(int val) {
        int idx = 0;
        while(idx < list.size()){
            if(list.get(idx).size() < capacity) break;
            idx++;
        }
        if(idx == list.size()) list.add(new ArrayDeque<>());
        Deque<Integer> cur = list.get(idx);
        cur.push(val);
        list.set(idx, cur);
    }
    
    public int pop() {
        int idx = list.size() - 1;
        while(idx > 0){
            if(list.get(idx).size() > 0) break;
            idx--;
        }
        if(idx == 0 && list.get(0).size() == 0) return -1; 
        Deque<Integer> cur = list.get(idx);
        int res = cur.poll();
        list.set(idx, cur);
        return res;
    }
    
    public int popAtStack(int idx) {
        if(idx > list.size()) return -1;
        Deque<Integer> cur = list.get(idx);
        if(cur.size() == 0) return -1;
        int res = cur.poll();
        list.set(idx, cur);
        return res;
    }
}

懒删除堆：

题解：https://leetcode.cn/problems/dinner-plate-stacks/solution/yu-qi-wei-hu-di-yi-ge-wei-man-zhan-bu-ru-sphs/

假如一开始连续执行了很多次 push 操作，就会得到一排整整齐齐的栈；然后再执行一些 popAtStack 操作，随机挑选 index，就会把这些栈弄得参差不齐。

这个时候再交替执行 push 和 popAtStack，「从左往右第一个没有满的栈」就没有什么规律可言了。如果把第一个未满栈填满，就要暴力寻找下一个未满栈了。

如何优化？

格局打开：与其维护第一个未满栈，不如维护所有未满栈。

假设可以用一个数据结构来维护这些未满栈（的下标），看看需要哪些操作：

• **对于 push 来说，需要知道这些下标中的最小值。**如果入栈后，栈满了，那么这个栈就不能算作未满栈，此时这个最小下标就需要从数据结构中移除

• 对于 popAtsStack 来说，如果操作的是一个满栈，操作后就得到了一个未满栈，那么就往数据结构中添加这个栈的下标

• 对于 pop 来说，它等价于 popAtStack(lastIndex)，其中lastIndex 是最后一个非空栈的下标

所以我们需要一个支持添加元素、查询最小值和移除最小值的数据结构。最小堆，就你了。

此外还需要一个列表 stacks，它的每个元素都是一个栈。上面说的lastIndex 就是 stacks 的长度减一。

如何维护 stacks 呢?

• 如果 push 时最小堆为空，说明所有栈都是满的，那么就需要向 stacks 的末尾添加一个新的栈。如果 capacity >1，就把这个新的未满栈的下标入堆

• 如果 popAtstack 操作的是最后一个栈，且操作后栈为空，那么就从 stacks 中移除最后一个栈。如果移除后 stacks 的最后一个栈也是空的，就不断移除直到 stacks 为空或者最后一个栈不为空。细节: 需要同步移除最小堆中的下标吗? 其实不需要如果在 push 时发现堆顶的下标大于等于 stacks 的长度，把整个堆清空即可。 (这个技巧叫懒删除。)

• 此外，如果 popAtstack 操作越界或者操作的栈为空，则返回 -1

问: 懒删除是否会导致堆中有重复的下标?

答: 不会有重复下标。

假设重复下标是在 push 时插入的，说明此前所有栈都是满的，堆中残留的下标必然都大于等于 stacks 的长度但这种情况下 push 会清空堆，不会导致重复下标。

假设重复下标是在 popAtstack 时插入的，这只会发生在 tackslindet 是满栈的情况下，而 push 保证在满栈时会去掉这个下标，所以也不会导致重复下标。

class DinnerPlates {
	// 懒删除堆：在pop元素时，该栈中 size=0 的时候不同步进行移除最小堆中的下标，只移除stacks列表中末尾的空栈
    // 		   在push时判断堆顶下标是否越界了(idx.peek() >= stacks.size())，越界则删除

    // 栈的容量
    private int capacity;
    // 所有栈
    private List<Deque<Integer>> stacks = new ArrayList<>();
    // 最小堆，保存未满栈的下标
    private PriorityQueue<Integer> idx = new PriorityQueue<>();

    public DinnerPlates(int capacity) {
        this.capacity = capacity;
    }
    
    public void push(int val) {
        if(!idx.isEmpty() && idx.peek() >= stacks.size())
            idx.clear(); // 堆中都是越界下标，直接清空(懒删除堆)
        if(idx.isEmpty()){ // 所有的栈都是满的
            Deque<Integer> st = new ArrayDeque<>();
            st.push(val);
            stacks.add(st); // 添加一个新的栈
            if(capacity > 1){ // 新的栈没有满
                idx.add(stacks.size() - 1); // 入堆
            }
        }else{ // 还有未满栈，在最小下标对应的栈中添加元素
            Deque<Integer> st = stacks.get(idx.peek());
            st.push(val);
            if(st.size() == capacity) { // 栈满了
                idx.poll(); // 从堆中去掉
            }
        }
    }
    
    public int pop() {
        // 等价为 popAtStack 最后一个非空栈
        return popAtStack(stacks.size() - 1);
    }
    
    public int popAtStack(int index) {
        if(index < 0 || index >= stacks.size() || stacks.get(index).isEmpty())
            return -1; // 非法操作
        Deque<Integer> st = stacks.get(index);
        if(st.size() == capacity){ // 满栈
            idx.add(index); // 弹出一个元素后，栈就不满了，把下标入堆
        }
        int val = st.pop();
        // 去掉末尾的空栈（懒删除，堆中下标在 push 时处理）
        while(!stacks.isEmpty() && stacks.get(stacks.size() - 1).isEmpty()){
            stacks.remove(stacks.size() - 1);
        }
        return val;
    }
}