The 2021 CCPC Weihai Onsite ADGJM
Dashboard - The 2021 CCPC Weihai Onsite - Codeforces
A. Goodbye, Ziyin!
思路
首先,根的度数必须 <= 2
然后,不能存在度数 > 3 的点
#include
#define int long long
constexpr int N = 1e6 + 10;
constexpr int mod = 998244353;
constexpr int Inf = 0x3f3f3f3f;
int n;
int d[N];
void solve() {
std::cin >> n;
for (int i = 1; i <= n - 1; i ++) {
int u, v;
std::cin >> u >> v;
d[u] ++;
d[v] ++;
}
int ans = 0;
bool ok = true;
for (int i = 1; i <= n; i ++) {
if (d[i] <= 2) ans ++;
if (d[i] > 3) ok = false;
}
if (!ok) std::cout << 0 << "\n";
else std::cout << ans << "\n";
}
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
while (t--) {
solve();
}
return 0;
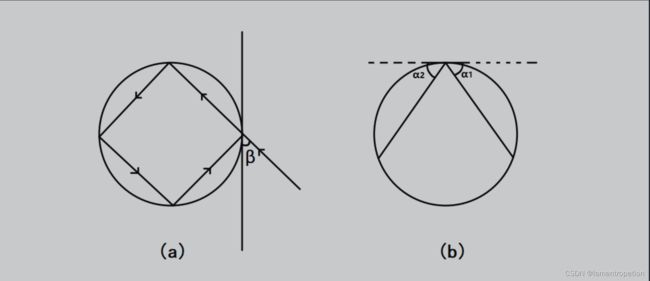
} J. Circular Billiard Table
#include
using namespace std;
#define fi first
#define se second
#define pb push_back
#define all(x) (x).begin(), (x).end()
#define int long long
const int mxn = 1e6+7;
int in[mxn];
void solve(){
int a, b;
cin >> a >> b;
cout << (180*b/__gcd(180*b,a))-1<<'\n';
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr), cout.tie(nullptr);
int T = 1;
cin >> T;
while(T--) solve();
return 0;
} D. Period
思路
首先周期 = 串长 - border,那问题转化为修改对 border集的影响
一开始border有很多,每次操作之后,border只剩下操作位置左边的所有border,因此可以考虑把所有border求出来,用差分数组维护即可
#include
using namespace std;
#define ll long long
const int mxn=1e6+10;
string s;
ll b[mxn],f[mxn],n,x,q;
void kmp(){
int j=0;
for(int i=2;i<=n;i++){
while(j&&s[i]!=s[j+1]) j=f[j];
if(s[j+1]==s[i]) j++;
f[i]=j;
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>s;
n=s.length();
s=" "+s;
kmp();
int j=n;
while(f[j]>=1){
b[f[j]]=1;
j=f[j];
}
for(int i=1;i<=n;i++) b[i]+=b[i-1];
cin>>q;
while(q--){
cin>>x;
x=min(x,n-x+1);
cout< G. Shinyruo and KFC
思路
很明显的组合思路,直接对于每种糖果去分配给队伍即可,即在 k 个队伍里选 ai 个分配
但是这样的复杂度是 nk 的,考虑优化
注意到 sigma ai <= 1e5,ai 的不同种类数是 sqrt(1e5) 级别的
因此考虑把相同 ai 的贡献打包计算
对于一排相同的 ai,需要再乘个幂次
#include
#define int long long
constexpr int N = 1e6 + 10;
constexpr int mod = 998244353;
constexpr int Inf = 0x3f3f3f3f;
int n, m;
int a[N];
int Fac[N], inv[N];
int qpow(int a, int b) {
int res = 1;
while(b) {
if (b & 1) res = (res * a) % mod;
a = (a * a) % mod;
b >>= 1;
}
return res;
}
int C(int n, int m) {
return Fac[n] * inv[m] % mod * inv[n - m] % mod;
}
void Fac_init() {
Fac[0] = 1;
for (int i = 1; i < N; i ++) {
Fac[i] = (Fac[i - 1] * i) % mod;
}
inv[N - 1] = qpow(Fac[N - 1], mod - 2);
for (int i = N - 2; i >= 0; i --) {
inv[i] = inv[i + 1] * (i + 1) % mod;
}
}
void solve() {
std::cin >> n >> m;
std::map mp;
int mx = 0;
for (int i = 1; i <= n; i ++) {
std::cin >> a[i];
mx = std::max(mx, a[i]);
mp[a[i]] ++;
}
for (int k = 1; k <= m; k ++) {
if (k < mx) {
std::cout << 0 << "\n";
continue;
}
int ans = 1;
for (auto [x, y] : mp) {
ans *= qpow(C(k, x), y);
ans %= mod;
}
std::cout << ans << "\n";
}
}
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
Fac_init();
while (t--) {
solve();
}
return 0;
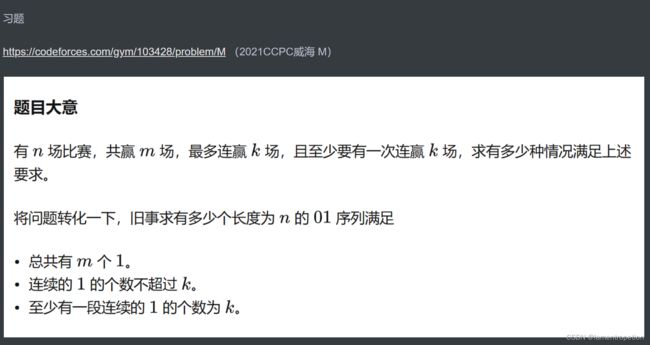
} M. 810975
#include
#define int long long
constexpr int N = 1e5 + 10;
constexpr int mod = 998244353;
constexpr int Inf = 0x3f3f3f3f;
int n, m, k;
int Fac[N], inv[N];
int C(int n, int m) {
return Fac[n] * inv[m] % mod * inv[n - m] % mod;
}
int qpow(int a, int b) {
int res = 1;
while(b) {
if (b & 1) res = (res * a) % mod;
a = (a * a) % mod;
b >>= 1;
}
return res;
}
void Fac_init() {
Fac[0] = 1;
for (int i = 1; i < N; i ++) Fac[i] = (Fac[i - 1] * i) % mod;
inv[N - 1] = qpow(Fac[N - 1], mod - 2);
for (int i = N - 2; i >= 0; i --) {
inv[i] = inv[i + 1] * (i + 1) % mod;
}
}
int calc(int k) {
int res = 0;
for (int i = 1; i * k <= m; i ++) {
if (i & 1) res = (res + C(n - m + 1, i) * C(n - i * k, n - m) % mod) % mod;
else res = (res - C(n - m + 1, i) * C(n - i * k , n - m) % mod ) % mod;
}
return res;
}
void solve() {
std::cin >> n >> m >> k;
if (k == 0) {
std::cout << (m == 0) << "\n";
return;
}
std::cout << ((calc(k) - calc(k + 1)) % mod + mod) % mod << "\n";
}
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
Fac_init();
while (t--) {
solve();
}
return 0;
}